Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T03:57:47.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Eigenvalues and strong orbit equivalence

Published online by Cambridge University Press:  21 July 2015

MARÍA ISABEL CORTEZ ,
FABIEN DURAND  and
SAMUEL PETITE
MARÍA ISABEL CORTEZ
Affiliation:
Departamento de Matemática y Ciencia de la Computación, Facultad de Ciencia, Universidad de Santiago de Chile, Av. Libertador Bernardo O’Higgins 3363, Santiago, Chile email [email protected] Fédération de Recherche ARC Mathématiques, CNRS-FR 3399, Université de Picardie Jules Verne, 33 rue Saint Leu, 80000 Amiens, France
FABIEN DURAND
Affiliation:
Laboratoire Amiénois de Mathématiques Fondamentales et Appliquées, CNRS-UMR 7352, Université de Picardie Jules Verne, 33 rue Saint Leu, 80000 Amiens, France email [email protected], [email protected]
SAMUEL PETITE
Affiliation:
Laboratoire Amiénois de Mathématiques Fondamentales et Appliquées, CNRS-UMR 7352, Université de Picardie Jules Verne, 33 rue Saint Leu, 80000 Amiens, France email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give conditions on the subgroups of the circle to be realized as the subgroups of eigenvalues of minimal Cantor systems belonging to a determined strong orbit equivalence class. Actually, the additive group of continuous eigenvalues 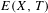$E(X,T)$ of the minimal Cantor system 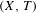$(X,T)$ is a subgroup of the intersection 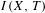$I(X,T)$ of all the images of the dimension group by its traces. We show, whenever the infinitesimal subgroup of the dimension group associated with 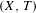$(X,T)$ is trivial, the quotient group 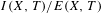$I(X,T)/E(X,T)$ is torsion free. We give examples with non-trivial infinitesimal subgroups where this property fails. We also provide some realization results.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 8 , December 2016 , pp. 2419 - 2440
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auslander, J.. Minimal Flows and their Extensions (North-Holland Mathematics Studies, 153) . North-Holland, Amsterdam, 1988, Notas de Matemática [Mathematical Notes], 122.Google Scholar
Boyle, M. and Handelman, D.. Entropy versus orbit equivalence for minimal homeomorphisms. Pacific J. Math. 164 (1994), 1–13.Google Scholar
Bressaud, X., Durand, F. and Maass, A.. Necessary and sufficient conditions to be an eigenvalue for linearly recurrent dynamical Cantor systems. J. Lond. Math. Soc. (2) 72 (2005), 799–816.Google Scholar
Bressaud, X., Durand, F. and Maass, A.. On the eigenvalues of finite rank Bratteli–Vershik dynamical systems. Ergod. Th. & Dynam. Sys. 30 (2010), 639–664.CrossRefGoogle Scholar
Cortez, M. I., Durand, F., Host, B. and Maass, A.. Continuous and measurable eigenfunctions of linearly recurrent dynamical Cantor systems. J. Lond. Math. Soc. (2) 67 (2003), 790–804.Google Scholar
Dartnell, P., Durand, F. and Maass, A.. Orbit equivalence and Kakutani equivalence with Sturmian subshifts. Studia Math. 142 (2000), 25–45.Google Scholar
Durand, F., Frank, A. and Maass, A.. Eigenvalues of Toeplitz minimal systems of finite topological rank. Ergod. Th. & Dynam. Sys. (2015), doi:10.1017/etds.2014.45.CrossRefGoogle Scholar
Dye, H.. On groups of measure preserving transformations I. Amer. J. Math. 81 (1959), 119–159.CrossRefGoogle Scholar
Effros, E., Handelman, D. and Shen, C.-L.. Dimension groups and their affine representations. Amer. J. Math. 102 (1980), 385–407.CrossRefGoogle Scholar
Effros, E. G.. Dimensions and C ∗ -algebras (CBMS Regional Conference Series in Mathematics, 46) . Conference Board of the Mathematical Sciences, Washington, DC, 1981.Google Scholar
Exel, R.. Rotation numbers for automorphisms of C ∗ algebras. Pacific J. Math. 127 (1987), 31–89.Google Scholar
Giordano, T., Putnam, I. and Skau, C. F.. Topological orbit equivalence and C ∗ -crossed products. Internat. J. Math. 469 (1995), 51–111.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101) . American Mathematical Society, Providence, RI, 2003.Google Scholar
Glasner, E. and Weiss, B.. Weak orbit equivalence of Cantor minimal systems. Internat. J. Math. 6 (1995), 559–579.Google Scholar
Herman, R. H., Putnam, I. and Skau, C. F.. Ordered Bratteli diagrams, dimension groups and topological dynamics. Internat. J. Math. 3 (1992), 827–864.Google Scholar
Itzá-Ortiz, B.. Eigenvalues, K-theory and minimal flows. Canad. J. Math. 59 (2007), 596–613.Google Scholar
Krieger, W.. On non-singular transformations of a measure space. I, II. Z. Wahrscheinlichkeitstheor. Verwandte Geb. 11 (1969), 83–97 ibid., 11 (1969), 98–119.CrossRefGoogle Scholar
Krieger, W.. On ergodic flows and the isomorphism of factors. Math. Ann. 223 (1976), 19–70.CrossRefGoogle Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics II. Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.CrossRefGoogle Scholar
Murray, F. J. and Von Neumann, J.. On rings of operators. Ann. of Math. (2) 7 (1936), 116–229.CrossRefGoogle Scholar
Olli, J.. Endomorphisms of Sturmian systems and the discrete chair substitution tiling system. Discrete Contin. Dyn. Syst. 33(9) (2013), 4173–4186.CrossRefGoogle Scholar
Ormes, N.. Strong orbit realization for minimal homeomorphisms. J. Anal. Math. 71 (1997), 103–133.Google Scholar
Ornstein, D. and Weiss, B.. Ergodic theory of amenable group actions. I. The Rohlin lemma. Bull. Amer. Math. Soc. (N.S.) 2 (1980), 161–164.Google Scholar
Packer, J.. K-theoretic invariants for C ∗ -algebras associated to transformations and induced flows. J. Funct. Anal. 67 (1986), 25–59.CrossRefGoogle Scholar
Petersen, K.. Ergodic Theory (Cambridge Studies in Advanced Mathematics, 2) . Cambridge University Press, Cambridge, 1983.Google Scholar
Renault, J.. C ⋆ -algebras and Dynamical Systems (27o  Colóquio Brasileiro de Matemática. [27th Brazilian Mathematics Colloquium]). Publicações Matemáticas do IMPA. [IMPA Mathematical Publications]. Instituto Nacional de Matemática Pura e Aplicada (IMPA), Rio de Janeiro, 2009.Google Scholar
Riedel, N.. Classification of the C ∗ -algebras associated with minimal rotations. Pacific J. Math. 101 (1982), 153–161.Google Scholar
Schwartzman, S.. Asymptotic cycles. Ann. of Math. (2) 66 (1957), 270–284.Google Scholar
Singer, I. M.. Automorphisms of finite factors. Amer. J. Math. 77 (1955), 117–133.Google Scholar
Sugisaki, F.. The relationship between entropy and strong orbit equivalence for the minimal homeomorphisms. I. Internat. J. Math. 14 (2003), 735–772.Google Scholar
Sugisaki, F.. Almost one-to-one extensions of Cantor minimal systems and order embeddings of simple dimension groups. Münster J. Math. 4 (2011), 141–169.Google Scholar
Tomiyama, J.. Invitation to C ∗ -algebras and Topological Dynamics (World Scientific Advanced Series in Dynamical Systems, 3) . World Scientific, Singapore, 1987.Google Scholar