Article contents
Dynamics of Newton maps
Published online by Cambridge University Press: 15 February 2022
Abstract
In this paper, we study the dynamics of the Newton maps for arbitrary polynomials. Let p be an arbitrary polynomial with at least three distinct roots, and f be its Newton map. It is shown that the boundary
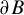 $\partial B$
of any immediate root basin B of f is locally connected. Moreover,
$\partial B$
of any immediate root basin B of f is locally connected. Moreover,
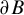 $\partial B$
is a Jordan curve if and only if
$\partial B$
is a Jordan curve if and only if
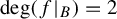 $\mathrm {deg}(f|_B)=2$
. This implies that the boundaries of all components of root basins, for the Newton maps for all polynomials, from the viewpoint of topology, are tame.
$\mathrm {deg}(f|_B)=2$
. This implies that the boundaries of all components of root basins, for the Newton maps for all polynomials, from the viewpoint of topology, are tame.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 5
- Cited by



