Published online by Cambridge University Press: 04 May 2021
This paper establishes the geometric rigidity of certain holomorphic correspondences in the family 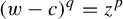 $(w-c)^q=z^p$
, whose post-critical set is finite in any bounded domain of
$(w-c)^q=z^p$
, whose post-critical set is finite in any bounded domain of 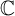 $\mathbb {C}$
. In spite of being rigid on the sphere, such correspondences are J-stable by means of holomorphic motions when viewed as maps of
$\mathbb {C}$
. In spite of being rigid on the sphere, such correspondences are J-stable by means of holomorphic motions when viewed as maps of 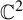 $\mathbb {C}^2$
. The key idea is the association of a conformal iterated function system to the return branches near the critical point, giving a global description of the post-critical set and proving the hyperbolicity of these correspondences.
$\mathbb {C}^2$
. The key idea is the association of a conformal iterated function system to the return branches near the critical point, giving a global description of the post-critical set and proving the hyperbolicity of these correspondences.