Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-20T10:37:28.194Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of compact quantum metric spaces

Part of: Linear spaces and algebras of operators Selfadjoint operator algebras

Published online by Cambridge University Press:  11 May 2020

JENS KAAD Open the ORCID record for JENS KAAD [Opens in a new window]  and
DAVID KYED Open the ORCID record for DAVID KYED [Opens in a new window]
JENS KAAD
Affiliation:
Department of Mathematics and Computer Science, University of Southern Denmark, Campusvej55, DK-5230 Odense M, Denmark email [email protected], [email protected]
DAVID KYED
Affiliation:
Department of Mathematics and Computer Science, University of Southern Denmark, Campusvej55, DK-5230 Odense M, Denmark email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide a detailed study of actions of the integers on compact quantum metric spaces, which includes general criteria ensuring that the associated crossed product algebra is again a compact quantum metric space in a natural way. Moreover, we provide a flexible set of assumptions ensuring that a continuous family of $\ast$-automorphisms of a compact quantum metric space yields a field of crossed product algebras which varies continuously in Rieffel’s quantum Gromov–Hausdorff distance. Finally, we show how our results apply to continuous families of Lip-isometric actions on compact quantum metric spaces and to families of diffeomorphisms of compact Riemannian manifolds which vary continuously in the Whitney 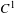$C^{1}$-topology.

Keywords

46L05quantum metric spacescrossed productsdynamics of Riemannian manifolds

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 46L89: Other “noncommutative” mathematics based on $C^*$-algebra theory 47L65: Crossed product algebras (analytic crossed products)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 7 , July 2021 , pp. 2069 - 2109
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aguilar, K. and Latrémolière, F.. Quantum ultrametrics on AF algebras and the Gromov-Hausdorff propinquity. Studia Math. 231(2) (2015), 149–193.Google Scholar
Blanchard, E.. Déformations de C ∗ -algèbres de Hopf. Bull. Soc. Math. France 124(1) (1996), 141–215.CrossRefGoogle Scholar
Bellissard, J., Marcolli, M. and Reihani, K.. Dynamical systems on spectral metric spaces. Preprint, 2010, arXiv:1008.4617 [math.OA].Google Scholar
Connes, A. and Dubois-Violette, M.. Noncommutative finite-dimensional manifolds. I. Spherical manifolds and related examples. Commun. Math. Phys. 230(3) (2002), 539–579.CrossRefGoogle Scholar
Connes, A. and Landi, G.. Noncommutative manifolds, the instanton algebra and isospectral deformations. Commun. Math. Phys. 221(1) (2001), 141–159.Google Scholar
Connes, A. and Moscovici, H.. The local index formula in noncommutative geometry. Geom. Funct. Anal. 5(2) (1995), 174–243.CrossRefGoogle Scholar
Connes, A. and Moscovici, H.. Type III and spectral triples. Traces in Number Theory, Geometry and Quantum Fields (Aspects of Mathematics, E38) . Ed. Albeverio, S.. Friedrich Vieweg, Wiesbaden, 2008, pp. 57–71.Google Scholar
Connes, A.. Compact metric spaces, Fredholm modules, and hyperfiniteness. Ergod. Th. & Dynam. Sys. 9(2) (1989), 207–220.CrossRefGoogle Scholar
Connes, A.. Noncommutative Geometry. Academic Press, San Diego, CA, 1994.Google Scholar
Connes, A.. Gravity coupled with matter and the foundation of non-commutative geometry. Commun. Math. Phys. 182(1) (1996), 155–176.CrossRefGoogle Scholar
Dixmier, J.. C ∗ -Algebras (North-Holland Mathematical Library, 15) . North-Holland, Amsterdam, 1977, translated from the French by F. Jellett.Google Scholar
Fell, J. M. G.. The structure of algebras of operator fields. Acta Math. 106 (1961), 233–280.CrossRefGoogle Scholar
Goffeng, M., Mesland, B. and Rennie, A.. Untwisting twisted spectral triples. Int. J. Math. 30(14) (2019), 1950076.CrossRefGoogle Scholar
Gromov, M.. Groups of polynomial growth and expanding maps. Publ. Math. Inst. Hautes Études Sci. 53 (1981), 53–73.Google Scholar
Hirsch, M. W.. Differential Topology (Graduate Texts in Mathematics, 33) . Springer, New York, 1994, corrected reprint of the 1976 original.Google Scholar
Higson, N. and Roe, J.. Analytic K-homology (Oxford Mathematical Monographs) . Oxford University Press, Oxford, 2000.Google Scholar
Hawkins, A., Skalski, A., White, S. and Zacharias, J.. On spectral triples on crossed products arising from equicontinuous actions. Math. Scand. 113(2) (2013), 262–291.CrossRefGoogle Scholar
Iochum, B. and Masson, T.. Crossed product extensions of spectral triples. J. Noncommut. Geom. 10(1) (2016), 65–133.Google Scholar
Kaad, J.. The unbounded Kasparov product by a differentiable module. J. Noncommut. Geom. to appear. Preprint, 2015, arXiv:1509.09063.Google Scholar
Kadison, R. V.. A Representation Theory for Commutative Topological Algebra (Memoirs of the American Mathematical Society, 7) . American Mathematical Society, Providence, RI, 1951.CrossRefGoogle Scholar
Kantorovitch, L. V.. On an effective method of solving extremal problems for quadratic functionals. C. R. Acad. Sci. URSS (N.S.) 48 (1945), 455–460.Google Scholar
Kadison, R. V. and Ringrose, J. R.. Fundamentals of the Theory of Operator Algebras. Vol. I (Graduate Studies in Mathematics, 15) . American Mathematical Society, Providence, RI, 1997, reprint of the 1983 original.CrossRefGoogle Scholar
Kantorovič, L. V. and Rubinšteĭn, G. V.. On a functional space and certain extremum problems. Dokl. Akad. Nauk SSSR (N.S.) 115 (1957), 1058–1061.Google Scholar
Kantorovič, L. V. and Rubinšteĭn, G. V.. On a space of completely additive functions. Vestn. Leningrad. Univ. 13(7) (1958), 52–59.Google Scholar
Kerr, D.. Matricial quantum Gromov-Hausdorff distance. J. Funct. Anal. 205(1) (2003), 132–167.CrossRefGoogle Scholar
Krähmer, U., Rennie, A. and Senior, R.. A residue formula for the fundamental Hochschild 3-cocycle for SU q(2). J. Lie Theory 22(2) (2012), 557–585.Google Scholar
Kupers, A.. Lectures on diffeomorphism groups of manifolds, 2019, http://www.math.harvard.edu/∼kupers/teaching/272x/book.pdf.Google Scholar
Lance, E. C.. Hilbert C ∗ -modules (London Mathematical Society Lecture Note Series, 210) . Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Latrémolière, F. and Packer, J.. Noncommutative solenoids. New York J. Math. 24A (2018), 155–191.Google Scholar
Latrémolière, F.. Approximation of quantum tori by finite quantum tori for the quantum Gromov-Hausdorff distance. J. Funct. Anal. 223(2) (2005), 365–395.CrossRefGoogle Scholar
Latrémolière, F.. Bounded-Lipschitz distances on the state space of a C ∗ -algebra. Taiwanese J. Math. 11(2) (2007), 447–469.CrossRefGoogle Scholar
Latrémolière, F.. Quantum locally compact metric spaces. J. Funct. Anal. 264(1) (2013), 362–402.CrossRefGoogle Scholar
Latrémolière, F.. The dual Gromov-Hausdorff propinquity. J. Math. Pures Appl. (9) 103(2) (2015), 303–351.CrossRefGoogle Scholar
Latrémolière, F.. The quantum Gromov-Hausdorff propinquity. Trans. Amer. Math. Soc. 368(1) (2016), 365–411.CrossRefGoogle Scholar
Latrémolière, F.. A compactness theorem for the dual Gromov-Hausdorff propinquity. Indiana Univ. Math. J. 66(5) (2017), 1707–1753.CrossRefGoogle Scholar
Lee, J. M.. Introduction to Riemannian Manifolds. Springer, Cham, 2018.CrossRefGoogle Scholar
Li, H.. $C^{\ast }$ -algebraic quantum Gromov–Hausdorff distance. Preprint, 2003, arXiv:0312003 [math.OA].Google Scholar
Li, H.. 𝜃-deformations as compact quantum metric spaces. Commun. Math. Phys. 256(1) (2005), 213–238.CrossRefGoogle Scholar
Li, H.. Order-unit quantum Gromov-Hausdorff distance. J. Funct. Anal. 231(2) (2006), 312–360.CrossRefGoogle Scholar
Li, H.. Compact quantum metric spaces and ergodic actions of compact quantum groups. J. Funct. Anal. 256(10) (2009), 3368–3408.CrossRefGoogle Scholar
Mesland, B. and Rennie, A.. Nonunital spectral triples and metric completeness in unbounded KK-theory. J. Funct. Anal. 271(9) (2016), 2460–2538.CrossRefGoogle Scholar
Moscovici, H.. Local index formula and twisted spectral triples. Quanta of Maths (Clay Mathematics Proceedings, 11) . American Mathematical Society, Providence, RI, 2010, pp. 465–500.Google Scholar
Paterson, A. L. T.. Contractive spectral triples for crossed products. Math. Scand. 114(2) (2014), 275–298.CrossRefGoogle Scholar
Pedersen, G. K.. C ∗ -Algebras and Their Automorphism Groups (London Mathematical Society Monographs, 14) . Academic Press, London, 1979.Google Scholar
Ponge, R. and Wang, H.. Noncommutative geometry and conformal geometry. I. Local index formula and conformal invariants. J. Noncommut. Geom. 12(4) (2018), 1573–1639.CrossRefGoogle Scholar
Rieffel, M. A.. Continuous fields of C ∗ -algebras coming from group cocycles and actions. Math. Ann. 283(4) (1989), 631–643.Google Scholar
Rieffel, M. A.. Metrics on states from actions of compact groups. Doc. Math. 3 (1998), 215–229.Google Scholar
Rieffel, M. A.. Metrics on state spaces. Doc. Math. 4 (1999), 559–600.Google Scholar
Rieffel, M. A.. Group C ∗ -algebras as compact quantum metric spaces. Doc. Math. 7 (2002), 605–651.Google Scholar
Rieffel, M. A.. Compact quantum metric spaces. Operator Algebras Quantization, and Noncommutative Geometry (Contemporary Mathematics, 365) . American Mathematical Society, Providence, RI, 2004, pp. 315–330.CrossRefGoogle Scholar
Rieffel, M. A.. Gromov-Hausdorff Distance for Quantum Metric Spaces (Memoirs of the American Mathematical Society, 168) . American Mathematical Society, Providence, RI, 2004, pp. 1–65.Google Scholar
Rieffel, M. A.. Matrix Algebras Converge to the Sphere for Quantum Gromov-Hausdorff Distance (Memoirs of the American Mathematical Society, 168) . American Mathematical Society, Providence, RI, 2004, pp. 67–91.Google Scholar