Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T04:15:06.080Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical simplices and Fraïssé theory

Published online by Cambridge University Press:  13 March 2018

JULIEN MELLERAY
JULIEN MELLERAY*
Affiliation:
Univ Lyon, Université Claude Bernard Lyon 1, CNRS UMR 5208, Institut Camille Jordan, F-69622 Villeurbanne, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We simplify a criterion (due to Ibarlucía and the author) which characterizes dynamical simplices, that is, sets 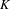$K$ of probability measures on a Cantor space 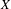$X$ for which there exists a minimal homeomorphism of 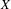$X$ whose set of invariant measures coincides with 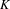$K$. We then point out that this criterion is related to Fraïssé theory, and use that connection to provide a new proof of Downarowicz’ theorem stating that any non-empty metrizable Choquet simplex is affinely homeomorphic to a dynamical simplex. The construction enables us to prove that there exist minimal homeomorphisms of a Cantor space which are speedup equivalent but not orbit equivalent, answering a question of Ash.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 11 , November 2019 , pp. 3111 - 3126
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ash, D.. Topological speedups, Preprint, 2015, arXiv:1605.08446.Google Scholar
Downarowicz, T.. The Choquet simplex of invariant measures for minimal flows. Israel J. Math. 74(2–3) (1991), 241–256.Google Scholar
Edwards, D. A.. Séparation des fonctions réelles définies sur un simplexe de Choquet. C. R. Acad. Sci. Paris 261 (1965), 2798–2800.Google Scholar
Fuchssteiner, B. and Lusky, W.. Convex Cones (North-Holland Mathematics Studies, 56) . North-Holland, Amsterdam, 1981.Google Scholar
Giordano, T., Putnam, I. F. and Skau, C. F.. Topological orbit equivalence and C ∗ -crossed products. J. Reine Angew. Math. 469 (1995), 51–111.Google Scholar
Glasner, E. and Weiss, B.. Weak orbit equivalence of Cantor minimal systems. Internat. J. Math. 6(4) (1995), 559–579.Google Scholar
Hodges, W.. Model Theory (Encyclopedia of Mathematics and its Applications, 42) . Cambridge University Press, Cambridge, 1993.Google Scholar
Ibarlucía, T. and Melleray, J.. Dynamical simplices and minimal homeomorphisms. Proc. Amer. Math. Soc. 145(11) (2017), 4981–4994.Google Scholar
Kechris, A. S. and Rosendal, C.. Turbulence, amalgamation and generic automorphisms of homogeneous structures. Proc. Lond. Math. Soc. (3) 94(2) (2007), 302–350.Google Scholar
Lindenstrauss, J.. Extension of compact operators. Mem. Amer. Math. Soc. 48 (1964), 112.Google Scholar
Namioka, I. and Phelps, R. R.. Tensor products of compact convex sets. Pacific J. Math. 31 (1969), 469–480.Google Scholar
Ormes, N. S.. Real coboundaries for minimal Cantor systems. Pacific J. Math. 195(2) (2000), 453–476.Google Scholar
Phelps, R. R.. Lectures on Choquet’s Theorem (Lecture Notes in Mathematics, 1757) , 2nd edn. Springer, Berlin, 2001.Google Scholar