Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-02T19:50:53.890Z Has data issue: false hasContentIssue false
  • English
  • Français

A dynamical characterization of diagonal-preserving $^{\ast }$-isomorphisms of graph 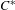$C^{\ast }$-algebras

Published online by Cambridge University Press:  02 May 2017

SARA E. ARKLINT ,
SØREN EILERS  and
EFREN RUIZ
SARA E. ARKLINT
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen, Denmark email [email protected], [email protected]
SØREN EILERS
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen, Denmark email [email protected], [email protected]
EFREN RUIZ
Affiliation:
Department of Mathematics, University of Hawaii, Hilo, 200 W. Kawili Street, Hilo, Hawaii, 96720-4091, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We characterize when there exists a diagonal-preserving $\ast$-isomorphism between two graph 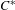$C^{\ast }$-algebras in terms of the dynamics of the boundary path spaces. In particular, we refine the notion of ‘orbit equivalence’ between the boundary path spaces of the directed graphs 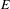$E$ and $F$ and show that this is a necessary and sufficient condition for the existence of a diagonal-preserving $\ast$-isomorphism between the graph 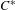$C^{\ast }$-algebras 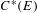$C^{\ast }(E)$ and 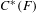$C^{\ast }(F)$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 7 , October 2018 , pp. 2401 - 2421
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharaman-Delaroche, C. and Renault, J.. Amenable Groupoids (Monographies de L’Enseignement Mathématique [Monographs of L’Enseignement Mathématique], 36) . L’Enseignement Mathématique, Geneva, 2000, with a foreword by Georges Skandalis and Appendix B by E. Germain.Google Scholar
Brownlowe, N., Carlsen, T. M. and Whittaker, M. F.. Graph algebras and orbit equivalence. Ergod. Th. & Dynam. Sys., to appear; doi:10.1017/etds.2015.52.Google Scholar
Carlsen, T. M., Ruiz, E. and Sims, A.. Equivalence and stable isomorphism of groupoids, and diagonal-preserving stable isomorphisms of graph $C^{\ast }$ -algebras and Leavitt path algebras. Proc. Amer. Math. Soc., to appear; doi:10.1090/proc/13321.Google Scholar
Carlsen, T. M. and Winger, M. L.. Orbit equivalence of graphs and isomorphism of graph groupoids. Preprint, 2016, arXiv:1610.09942.Google Scholar
Eilers, S., Restorff, G., Ruiz, E. and Sørensen, A. P. W.. Geometric classification of graph $C^{\ast }$ -algebras over finite graphs. Preprint, 2016, arXiv:1604.05439.Google Scholar
Matsumoto, K.. Classification of Cuntz–Krieger algebras by orbit equivalence of topological Markov shifts. Proc. Amer. Math. Soc. 141 (2013), 2329–2342.Google Scholar
Matsumoto, K. and Matui, H.. Continuous orbit equivalence of topological Markov shifts and Cuntz–Krieger algebras. Kyoto J. Math. 54(4) (2014), 863–877.Google Scholar
Renault, J.. Cartan subalgebras in C ∗ -algebras. Irish Math. Soc. Bull. 61 (2008), 29–63.Google Scholar
Rørdam, M.. Classification of Cuntz–Krieger algebras. K-Theory 9(1) (1995), 31–58.Google Scholar
Szymański, W.. General Cuntz–Krieger uniqueness theorem. Internat. J. Math. 13(5) (2002), 549–555.Google Scholar
Webster, S. B. G.. The path space of a directed graph. Proc. Amer. Math. Soc. 142(1) (2014), 213–225.Google Scholar
Yeend, T.. Groupoid models for the C ∗ -algebras of topological higher-rank graphs. J. Operator Theory 57(1) (2007), 95–120.Google Scholar