Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-02T19:00:07.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Directed harmonic currents near hyperbolic singularities

Published online by Cambridge University Press:  02 May 2017

VIÊT-ANH NGUYÊN
VIÊT-ANH NGUYÊN*
Affiliation:
Université de Lille 1, Laboratoire de mathématiques Paul Painlevé, CNRS UMR 8524, 59655 Villeneuve d’Ascq Cedex, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

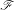Let $\mathscr{F}$ be a holomorphic foliation by curves defined in a neighborhood of $0$ in 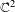$\mathbb{C}^{2}$ having $0$ as a hyperbolic singularity. Let $T$ be a harmonic current directed by 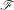$\mathscr{F}$ which does not give mass to any of the two separatrices. We show that the Lelong number of $T$ at $0$ vanishes. Then we apply this local result to investigate the global mass distribution for directed harmonic currents on singular holomorphic foliations living on compact complex surfaces. Finally, we apply this global result to study the recurrence phenomenon of a generic leaf.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 8 , December 2018 , pp. 3170 - 3187
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berndtsson, B. and Sibony, N.. The ∂ -equation on a positive current. Invent. Math. 147(2) (2002), 371–428.Google Scholar
Dinh, T.-C., Nguyên, V.-A. and Sibony, N.. Heat equation and ergodic theorems for Riemann surface laminations. Math. Ann. 354(1) (2012), 331–376.Google Scholar
Dinh, T.-C., Nguyên, V.-A. and Sibony, N.. Entropy for hyperbolic Riemann surface laminations II. Frontiers in Complex Dynamics: A Volume in Honor of John Milnor’s 80th Birthday. Eds. Bonifant, A., Lyubich, M. and Sutherland, S.. Princeton University Press, Princeton, NJ, 2012, p. 29.Google Scholar
Dinh, T.-C. and Sibony, N.. Unique ergodicity for foliations in $\mathbb{P}^{2}$ with an invariant curve. Preprint, 2015, arXiv:1509.07711, 28 pp.Google Scholar
Fornæss, J. E. and Sibony, N.. Harmonic currents of finite energy and laminations. Geom. Funct. Anal. 15(5) (2005), 962–1003.Google Scholar
Fornæss, J. E. and Sibony, N.. Riemann surface laminations with singularities. J. Geom. Anal. 18(2) (2008), 400–442.Google Scholar
Fornæss, J. E. and Sibony, N.. Unique ergodicity of harmonic currents on singular foliations of ℙ2 . Geom. Funct. Anal. 19(5) (2010), 1334–1377.Google Scholar
Glutsyuk, A. A.. Hyperbolicity of the leaves of a generic one-dimensional holomorphic foliation on a nonsingular projective algebraic variety. Tr. Mat. Inst. Steklova 213 (1997), Differ. Uravn. s Veshchestv. i Kompleks. Vrem., 90–111 (Russian); translation in Proc. Steklov Inst. Math. 1996, 213, 83–103.Google Scholar
Lins Neto, A.. Uniformization and the Poincaré metric on the leaves of a foliation by curves. Bol. Soc. Brasil. Mat. (N.S.) 31(3) (2000), 351–366.Google Scholar
Lins Neto, A. and Soares, M. G.. Algebraic solutions of one-dimensional foliations. J. Differential Geom. 43(3) (1996), 652–673.Google Scholar
Nguyen, V.-A.. Singular holomorphic foliations by curves I: Integrability of holonomy cocycle in dimension 2. Preprint, 2014, arXiv:1403.7688, 73 pp.Google Scholar
Skoda, H.. Prolongement des courants, positifs, fermés de masse finie [Extension of closed, positive currents of finite mass]. Invent. Math. 66(3) (1982), 361–376 (French).Google Scholar