Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Elliott, George A.
1994.
Algebraic Methods in Operator Theory.
p.
109.
Elliott, George A.
1995.
Proceedings of the International Congress of Mathematicians.
p.
922.
Rørdam, Mikael
1995.
Classification of Cuntz-Krieger algebras.
K-Theory,
Vol. 9,
Issue. 1,
p.
31.
Bédos, Erik
1996.
Simple C*-crossed products with a unique trace.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 3,
p.
415.
Kishimoto, A.
1996.
A Rohlin property for one-parameter automorphism groups.
Communications in Mathematical Physics,
Vol. 179,
Issue. 3,
p.
599.
Kishimoto, A
1998.
Unbounded Derivations in AT Algebras.
Journal of Functional Analysis,
Vol. 160,
Issue. 1,
p.
270.
Brown, Nathanial P
1998.
AF Embeddability of Crossed Products of AF Algebras by the Integers.
Journal of Functional Analysis,
Vol. 160,
Issue. 1,
p.
150.
KISHIMOTO, A.
2000.
ROHLIN PROPERTY FOR SHIFT AUTOMORPHISMS.
Reviews in Mathematical Physics,
Vol. 12,
Issue. 07,
p.
965.
Bratteli, Ola
and
Kishimoto, Akitaka
2000.
Homogeneity of the Pure State Space of the Cuntz Algebra.
Journal of Functional Analysis,
Vol. 171,
Issue. 2,
p.
331.
Kirchberg, E.
and
Phillips, N. Ch.
2000.
Embedding of exact C* -algebras in the Cuntz algebra 𝒪2.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2000,
Issue. 525,
p.
17.
KISHIMOTO, A.
2001.
UHF FLOWS AND THE FLIP AUTOMORPHISM.
Reviews in Mathematical Physics,
Vol. 13,
Issue. 09,
p.
1163.
KISHIMOTO, AKITAKA
2002.
ROHLIN FLOWS ON THE CUNTZ ALGEBRA ${\mathcal O}_2$.
International Journal of Mathematics,
Vol. 13,
Issue. 10,
p.
1065.
Rørdam, M.
2002.
Classification of Nuclear C*-Algebras. Entropy in Operator Algebras.
Vol. 126,
Issue. ,
p.
1.
Størmer, E.
2002.
Classification of Nuclear C*-Algebras. Entropy in Operator Algebras.
Vol. 126,
Issue. ,
p.
147.
Kishimoto, A.
2003.
Non-commutative shifts and crossed products.
Journal of Functional Analysis,
Vol. 200,
Issue. 2,
p.
281.
Izumi, Masaki
2004.
Finite group actions on C∗-algebras with the Rohlin property—II.
Advances in Mathematics,
Vol. 184,
Issue. 1,
p.
119.
Izumi, Masaki
2004.
Finite group actions on C*-algebras with the Rohlin property, I.
Duke Mathematical Journal,
Vol. 122,
Issue. 2,
Holton, Charles G.
2005.
The Rohlin property for shifts of finite type.
Journal of Functional Analysis,
Vol. 229,
Issue. 2,
p.
277.
Kerr, David
and
Li, Hanfeng
2007.
Independence in topological and C*-dynamics.
Mathematische Annalen,
Vol. 338,
Issue. 4,
p.
869.
Lin, Huaxin
2007.
Weak Semiprojectivity in Purely Infinite SimpleC*-Algebras.
Canadian Journal of Mathematics,
Vol. 59,
Issue. 2,
p.
343.


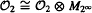 where
where  is the Cuntz algebra of order 2.
is the Cuntz algebra of order 2.