Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Avigad, Jeremy
2009.
The metamathematics of ergodic theory.
Annals of Pure and Applied Logic,
Vol. 157,
Issue. 2-3,
p.
64.
Foreman, Matthew
2010.
Models for measure preserving transformations.
Topology and its Applications,
Vol. 157,
Issue. 8,
p.
1404.
Foreman, Matthew
and
Weiss, Benjamin
2019.
A symbolic representation for Anosov–Katok systems.
Journal d'Analyse Mathématique,
Vol. 137,
Issue. 2,
p.
603.
Glasner, Eli
and
Weiss, Benjamin
2021.
A generic distal tower of arbitrary countable height over an arbitrary infinite ergodic system.
Journal of Modern Dynamics,
Vol. 17,
Issue. 0,
p.
435.
Kanigowski, Adam
Vinhage, Kurt
and
Wei, Daren
2021.
Kakutani equivalence of unipotent flows.
Duke Mathematical Journal,
Vol. 170,
Issue. 7,
WEI, DAREN
2022.
Kakutani equivalence for products of some special flows over rotations.
Ergodic Theory and Dynamical Systems,
Vol. 42,
Issue. 4,
p.
1548.
Foreman, Matthew
2022.
Encyclopedia of Complexity and Systems Science.
p.
1.
Banerjee, Shilpak
and
Kunde, Philipp
2022.
Real-analytic realization of Uniform Circular Systems and some applications.
Journal d'Analyse Mathématique,
Vol. 148,
Issue. 2,
p.
399.
Foreman, Matthew
and
Weiss, Benjamin
2022.
Odometer Based Systems.
Israel Journal of Mathematics,
Vol. 251,
Issue. 1,
p.
327.
GERBER, MARLIES
and
KUNDE, PHILIPP
2022.
Loosely Bernoulli odometer-based systems whose corresponding circular systems are not loosely Bernoulli.
Ergodic Theory and Dynamical Systems,
Vol. 42,
Issue. 3,
p.
917.
JAMNESHAN, ASGAR
2023.
An uncountable Furstenberg–Zimmer structure theory.
Ergodic Theory and Dynamical Systems,
Vol. 43,
Issue. 7,
p.
2404.
Foreman, Matthew
2023.
Ergodic Theory.
p.
529.
Gerber, Marlies
and
Kunde, Philipp
2025.
Non-classifiability of ergodic flows up to time change.
Inventiones mathematicae,
Vol. 239,
Issue. 2,
p.
527.


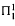 -norm. Various other results about skew products are also shown.
-norm. Various other results about skew products are also shown.