Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T04:42:46.164Z Has data issue: false hasContentIssue false
  • English
  • Français

Closed orbits in quotient systems

Published online by Cambridge University Press:  12 May 2016

STEFANIE ZEGOWITZ
STEFANIE ZEGOWITZ*
Affiliation:
University of Exeter, College of Engineering, Mathematics, and Physical Sciences, Harrison Building, North Park Road, ExeterEX4 4QF, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the relationship between pairs of topological dynamical systems 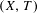$(X,T)$ and 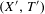$(X^{\prime },T^{\prime })$, where 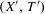$(X^{\prime },T^{\prime })$ is the quotient of 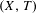$(X,T)$ under the action of a finite group 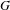$G$. We describe three phenomena concerning the behaviour of closed orbits in the quotient system, and the constraints given by these phenomena. We find upper and lower bounds for the extremal behaviour of closed orbits in the quotient system in terms of properties of 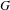$G$ and show that any growth rate in between these bounds can be achieved.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 7 , October 2017 , pp. 2337 - 2352
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Jaidee, S., Stevens, S. and Ward, T.. Mertens’ theorem for toral automorphisms. Proc. Amer. Math. Soc. 139(5) (2011), 1819–1824.Google Scholar
Md Noorani, M. S.. Mertens theorem and closed orbits of ergodic toral automorphisms. Bull. Malays. Math. Sci. Soc. (2) 22(2) (1999), 127–133.Google Scholar
Parry, W.. An analogue of the prime number theorem for closed orbits of shifts of finite type and their suspensions. Israel J. Math. 45(1) (1983), 41–52.Google Scholar
Parry, W. and Pollicott, M.. An analogue of the prime number theorem for closed orbits of Axiom A flows. Ann. of Math. (2) 118(3) (1983), 573–591.Google Scholar
Puri, Y. and Ward, T.. Arithmetic and growth of periodic orbits. J. Integer Seq. 4(2) (2001), Article 01.2.1, 18 pp.Google Scholar
Sharp, R.. An analogue of Mertens’ theorem for closed orbits of Axiom A flows. Bol. Soc. Brasil. Mat. (N.S.) 21(2) (1991), 205–229.Google Scholar
Sharp, R.. Prime orbit theorems with multi-dimensional constraints for Axiom A flows. Monatsh. Math. 114(3–4) (1992), 261–304.Google Scholar
Stevens, S., Ward, T. and Zegowitz, S.. Halving dynamical systems. Contemp. Math. to appear, Preprint,arXiv:1407.7787.Google Scholar
Waddington, S.. The prime orbit theorem for quasihyperbolic toral automorphisms. Monatsh. Math. 112(3) (1991), 235–248.Google Scholar
Windsor, A. J.. Smoothness is not an obstruction to realizability. Ergod. Th. & Dynam. Sys. 28(3) (2008), 1037–1042.CrossRefGoogle Scholar
Zegowitz, S.. Closed orbits in quotient system. PhD Thesis, University of East Anglia, 2015.Google Scholar