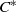 ${C}^{\ast } $-algebras
${C}^{\ast } $-algebrasPublished online by Cambridge University Press: 28 August 2013
We consider a construction of 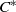 ${C}^{\ast } $-algebras from continuous piecewise monotone maps on the circle which generalizes the crossed product construction for homeomorphisms and more generally the construction of Renault, Deaconu and Anantharaman-Delaroche for local homeomorphisms. Assuming that the map is surjective and not locally injective we give necessary and sufficient conditions for the simplicity of the
${C}^{\ast } $-algebras from continuous piecewise monotone maps on the circle which generalizes the crossed product construction for homeomorphisms and more generally the construction of Renault, Deaconu and Anantharaman-Delaroche for local homeomorphisms. Assuming that the map is surjective and not locally injective we give necessary and sufficient conditions for the simplicity of the 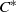 ${C}^{\ast } $-algebra and show that it is then a Kirchberg algebra. We provide tools for the calculation of the
${C}^{\ast } $-algebra and show that it is then a Kirchberg algebra. We provide tools for the calculation of the 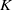 $K$-theory groups and turn them into an algorithmic method for Markov maps.
$K$-theory groups and turn them into an algorithmic method for Markov maps.