Hostname: page-component-f554764f5-rj9fg Total loading time: 0 Render date: 2025-04-21T13:19:41.170Z Has data issue: false hasContentIssue false
  • English
  • Français

Cancellations of periodic orbits for non-singular Morse–Smale flows

Part of: Topological dynamics Spectral sequences Smooth dynamical systems: general theory Applied homological algebra and category theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  25 May 2023

D. V. S. LIMA Open the ORCID record for D. V. S. LIMA [Opens in a new window] ,
K. A. DE REZENDE Open the ORCID record for K. A. DE REZENDE [Opens in a new window]  and
M. R. DA SILVEIRA Open the ORCID record for M. R. DA SILVEIRA [Opens in a new window]
D. V. S. LIMA
Affiliation:
Federal University of the ABC, Center of Mathematics Computing and Cognition, Santo Andre, Brazil (e-mail: [email protected])
K. A. DE REZENDE
Affiliation:
University of Campinas, Institute of Mathematics, Statistics and Scientific Computing, Campinas, Brazil e-mail: ([email protected])
M. R. DA SILVEIRA*
Affiliation:
Federal University of the ABC, Center of Mathematics Computing and Cognition, Santo Andre, Brazil (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work, we explore the dynamical implications of a spectral sequence analysis of a filtered chain complex associated to a non-singular Morse–Smale (NMS) flow 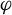$\varphi $ on a closed orientable 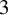$3$-manifold 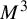$M^3$ with no heteroclinic trajectories connecting saddle periodic orbits. We introduce the novel concepts of cancellations and reductions of pairs of periodic orbits based on Franks’ morsification and Smale’s cancellation theorems. The main goal is to establish an algebraic-dynamical correspondence between the unfolding of this spectral sequence associated to 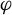$\varphi $ and a family of flows obtained by cancelling and reducing pairs of periodic orbits of 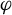$\varphi $ on 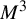$M^3$. This correspondence is achieved through a spectral sequence sweeping algorithm (SSSA), which determines the order in which these cancellations and reductions of periodic orbits occur, producing a family of NMS flows that reaches a core flow when the spectral sequence converges.

Keywords

non-singular Morse–Smale flowsMorse chain complex3-manifoldsspectral sequencescancellation of critical points

MSC classification

Primary: 37C27: Periodic orbits of vector fields and flows 37D15: Morse-Smale systems 55T05: General
Secondary: 37B35: Gradient-like and recurrent behavior; isolated (locally maximal) invariant sets 37B30: Index theory, Morse-Conley indices 55U15: Chain complexes
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 4 , April 2024 , pp. 1123 - 1171
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Asimov, D.. Round handles and non-singular Morse–Smale flows. Ann. of Math. (2) 102 (1975), 41–54.CrossRefGoogle Scholar
Bertolim, M. A., de Rezende, K. A. and Manzoli Neto, O.. Isolating blocks for periodic orbits. J. Dyn. Control Syst. 13(1) (2007) 121–134.Google Scholar
Bertolim, M. A., Lima, D. V. S., Mello, M. P., de Rezende, K. A. and da Silveira, M. R.. A global two-dimensional version of Smale s cancellation theorem via spectral sequences. Ergod. Th. & Dynam. Sys. 36(6) (2016), 1795–1838.Google Scholar
Bertolim, M. A., Lima, D. V. S., Mello, M. P., de Rezende, K. A. and da Silveira, M. R.. Algebraic and dynamical cancellations associated to a spectral sequence. Eur. J. Math. 3 (2017), 387–428.CrossRefGoogle Scholar
Campos, B. and Vindel, P.. Fat handles and phase portraits of non singular Morse–Smale flows on S3 with Unknotted saddle orbits. Adv. Nonlinear Stud. 14(3) (2014), 605–617.Google Scholar
Cornea, O., de Rezende, K. A. and da Silveira, M. R.. Spectral sequences in Conley’s theory. Ergod. Th. & Dynam. Sys. 30(4) (2010), 1009–1054.Google Scholar
Davis, J. F. and Kirk, P.. Lecture Notes in Algebraic Topology (Graduate Studies in Mathematics, 35). American Mathematical Society, Providence, RI, 2001.Google Scholar
Franks, J.. The periodic structure of non-singular Morse–Smale flows. Comment. Math. Helv. 53(1) (1978), 279–294.Google Scholar
Franks, J.. Morse Smale flows and homotopy theory. Topology 18(3) (1979), 199–215.Google Scholar
Franks, J.. Homology and Dynamical Systems (CBMS Regional Conference Series in Mathematics, 49). American Mathematical Society, Providence, RI, 1982.Google Scholar
Franks, J.. Nonsingular Smale flows on ${S}^3$ . Topology 24(3) (1985), 265–282.Google Scholar
Grines, V., Gurevich, E., Pochinka, O. and Zhuzhoma, E.. Classification of Morse–Smale systems and topological structure of the underlying manifolds. Russian Math. Surveys 74(1) (2019), 37–110.CrossRefGoogle Scholar
Jaco, W. H.. Lectures on Three-Manifold Topology (CBMS Regional Conference Series in Mathematics, 43). American Mathematical Society, Providence, RI, 1980.Google Scholar
Lima, D. V. S. and de Rezende, K. A.. Connection matrices for Morse–Bott flows. Topol. Methods Nonlinear Anal. 44(2) (2014), 471–495.Google Scholar
Lima, D. V. S., Mazoli Neto, O., de Rezende, K. A. and da Silveira, M. R.. Cancellations for circle-valued Morse functions via spectral sequences. Topol. Methods Nonlinear Anal. 51(1) (2018), 259–311.Google Scholar
Lima, D. V. S., Raminelli, S. A. and de Rezende, K. A.. Homotopical cancellation theory for Gutierrez–Sotomayor singular flows. J. Singul. 23 (2021), 33–91.Google Scholar
Matveev, S. V.. Algorithmic Topology and Classification of 3-Manifolds (Algorithms and Computation in Mathematics, 9). Springer, Berlin, 2007.Google Scholar
Milnor, J.. Lectures on the H-Cobordism. Princeton University Press, Princeton, NJ, 1965.Google Scholar
Morgan, J.. Non-singular Morse–Smale flows in 3-dimensional manifolds. Topology 18 (1978), 41–53.Google Scholar
Pochinka, O. V. and Shubin, D. D.. Non-singular Morse–Smale flows on $n$ -manifolds with attractor-repeller dynamics. Nonlinearity 35(3) (2022), 1485.Google Scholar
Salamon, D. A.. The Morse theory, the Conley index and the Floer homology. Bull. Lond. Math. Soc. 22 (1990), 113–240.Google Scholar
Spanier, E.. Algebraic Topology. McGraw-Hill, New York, NY, 1966.Google Scholar
Wada, M.. Closed orbits of non-singular Morse–Smale flows on S3. J. Math. Soc. Japan 41(3) (1989), 405–413.Google Scholar
Weber, J.. The Morse–Witten complex via dynamical systems. Expo. Math. 24 (2006), 127–159.Google Scholar