Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-13T12:25:42.689Z Has data issue: false hasContentIssue false
  • English
  • Français

The 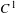$C^{1}$ property of convex carrying simplices for competitive maps

Part of: Smooth dynamical systems: general theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  17 October 2018

JANUSZ MIERCZYŃSKI Open the ORCID record for JANUSZ MIERCZYŃSKI [Opens in a new window]
JANUSZ MIERCZYŃSKI*
Affiliation:
Faculty of Pure and Applied Mathematics, Wrocław University of Science and Technology, Wybrzeże Wyspiańskiego 27, PL-50-370 Wrocław, Poland email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a class of competitive maps there is an invariant one-codimensional manifold (the carrying simplex) attracting all non-trivial orbits. In this paper it is shown that its convexity implies that it is a 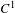$C^{1}$ submanifold-with-corners, neatly embedded in the non-negative orthant. The proof uses the characterization of neat embedding in terms of inequalities between Lyapunov exponents for ergodic invariant measures supported on the boundary of the carrying simplex.

Keywords

smooth dynamics

MSC classification

Primary: 37C65: Monotone flows 37D10: Invariant manifold theory 37D30: Partially hyperbolic systems and dominated splittings
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 5 , May 2020 , pp. 1335 - 1350
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliprantis, C. D. and Border, K. C.. Infinite Dimensional Analysis. A Hitchhiker’s Guide, 3rd edn. Springer, Berlin, 2006.Google Scholar
Arnold, L.. Random Dynamical Systems (Springer Monographs in Mathematics). Springer, Berlin, 1998.Google Scholar
Baigent, S.. Convexity preserving flows of totally competitive planar Lotka–Volterra equations and the geometry of the carrying simplex. Proc. Edinb. Math. Soc. (2) 55(1) (2012), 53–63.Google Scholar
Baigent, S.. Geometry of carrying simplices of 3-species competitive Lotka–Volterra systems. Nonlinearity 26(4) (2013), 1001–1029.Google Scholar
Baigent, S.. Convexity of the carrying simplex for discrete-time planar competitive Kolmogorov systems. J. Difference Equ. Appl. 22(5) (2016), 609–622.Google Scholar
Balreira, E. C., Elaydi, S. and Luís, R.. Global stability of higher dimensional monotone maps. J. Difference Equ. Appl. 23(12) (2017), 2037–2071.Google Scholar
Benaïm, M.. On invariant hypersurfaces of strongly monotone maps. J. Differential Equ. 137(2) (1997), 302–319.Google Scholar
Brunovský, P.. Controlling nonuniqueness of local invariant manifolds. J. Reine Angew. Math. 446 (1994), 115–135.Google Scholar
Hirsch, M. W.. Systems of differential equations which are competitive or cooperative. III. Competing species. Nonlinearity 1(1) (1988), 51–71.Google Scholar
Hirsch, M. W.. On existence and uniqueness of the carrying simplex for competitive dynamical systems. J. Biol. Dyn. 2 (2008), 169–179.Google Scholar
Jiang, J., Mierczyński, J. and Wang, Y.. Smoothness of the carrying simplex for discrete-time competitive dynamical systems: a characterization of neat embedding. J. Differential Equ. 246(4) (2009), 1623–1672.Google Scholar
Jiang, J. and Niu, L.. On the equivalent classification of three-dimensional competitive Leslie/Gower models via the boundary dynamics on the carrying simplex. J. Math. Biol. 74(5) (2017), 1223–1261.Google Scholar
Jiang, J., Niu, L. and Wang, Y.. On heteroclinic cycles of competitive maps via carrying simplices. J. Math. Biol. 72(4) (2016), 939–972.Google Scholar
Lian, Z. and Lu, K.. Lyapunov Exponents and Invariant Manifolds for Random Dynamical Systems on a Banach Space (Memoirs of the American Mathematical Society, 206). American Mathematical Society, Providence, RI, 2010, p. 967.Google Scholar
Marszczewska, K.. Approximation of carrying simplices in competitive Lotka–Volterra systems (in Polish). MSc Dissertation, Institute of Mathematics and Computer Science, Wrocław University of Technology, 2005.Google Scholar
Mierczyński, J.. The C 1 property of carrying simplices for a class of competitive systems of ODEs. J. Differential Equ. 111(2) (1994), 385–409.Google Scholar
Mierczyński, J.. Smoothness of carrying simplices for three-dimensional competitive systems: a counterexample. Dyn. Contin. Discrete Impuls. Syst. 6(1) (1999), 149–154.Google Scholar
Mierczyński, J.. On peaks in carrying simplices. Colloq. Math. 81(2) (1999), 285–292.Google Scholar
Mierczyński, J.. The C 1 property of convex carrying simplices for three-dimensional competitive maps. J. Difference Equ. Appl. 24(8) (2018), 1199–1209.Google Scholar
Mierczyński, J. and Schreiber, S. J.. Kolmogorov vector fields with robustly permanent subsystems. J. Math. Anal. Appl. 267(1) (2002), 329–337.Google Scholar
Niu, L. and Ruiz-Herrera, A.. Trivial dynamics in discrete-time systems: carrying simplex and translation arcs. Nonlinearity 31(6) (2018), 2633–2650.Google Scholar
Ruiz-Herrera, A.. Exclusion and dominance in discrete population models via the carrying simplex. J. Difference Equ. Appl. 19(1) (2013), 96–113.Google Scholar
Smale, S.. On the differential equations of species in competition. J. Math. Biol. 3 (1976), 5–7.Google Scholar
Smith, H. L.. Periodic competitive differential equations and the discrete dynamics of competitive maps. J. Differential Equ. 64(2) (1986), 165–194.Google Scholar
Tineo, A.. On the convexity of the carrying simplex of planar Lotka–Volterra competitive systems. Appl. Math. Comput. 123(1) (2001), 93–108.Google Scholar
Wang, Y. and Jiang, J.. Uniqueness and attractivity of the carrying simplex for discrete-time competitive dynamical systems. J. Differential Equ. 186(2) (2002), 611–632.Google Scholar
Zeeman, E. C. and Zeeman, M. L.. On the convexity of carrying simplices in competitive Lotka–Volterra systems. Differential Equations, Dynamical Systems, and Control Science (Lecture Notes in Pure and Applied Mathematics, 152). Dekker, New York, 1994, pp. 353–364.Google Scholar
Zeeman, E. C. and Zeeman, M. L.. From local to global behavior in competitive Lotka–Volterra systems. Trans. Amer. Math. Soc. 355(2) (2003), 713–734.Google Scholar
Zeeman, M. L.. Hopf bifurcations in competitive three-dimensional Lotka–Volterra systems. Dynam. Stab. Syst. 8(3) (1993), 189–217.Google Scholar