Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T04:15:46.991Z Has data issue: false hasContentIssue false
  • English
  • Français

Amenable dynamical systems over locally compact groups

Part of: Selfadjoint operator algebras Linear spaces and algebras of operators

Published online by Cambridge University Press:  25 June 2021

ALEX BEARDEN  and
JASON CRANN Open the ORCID record for JASON CRANN [Opens in a new window]
ALEX BEARDEN
Affiliation:
Department of Mathematics, University of Texas at Tyler, Tyler, TX 75799, USA (e-mail: [email protected])
JASON CRANN*
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, Ontario, CanadaK1S 5B6
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish several new characterizations of amenable 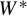$W^*$ - and 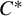$C^*$ -dynamical systems over arbitrary locally compact groups. In the 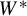$W^*$ -setting we show that amenability is equivalent to (1) a Reiter property and (2) the existence of a certain net of completely positive Herz–Schur multipliers of 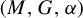$(M,G,\alpha )$ converging point weak* to the identity of 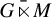$G\bar {\ltimes }M$ . In the 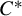$C^*$ -setting, we prove that amenability of 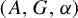$(A,G,\alpha )$ is equivalent to an analogous Herz–Schur multiplier approximation of the identity of the reduced crossed product 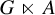$G\ltimes A$ , as well as a particular case of the positive weak approximation property of Bédos and Conti [On discrete twisted 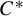$C^*$ -dynamical systems, Hilbert 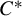$C^*$ -modules and regularity. Münster J. Math.5 (2012), 183–208] (generalized to the locally compact setting). When $Z(A^{**})=Z(A)^{**}$ , it follows that amenability is equivalent to the 1-positive approximation property of Exel and Ng [Approximation property of 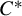$C^*$ -algebraic bundles. Math. Proc. Cambridge Philos. Soc.132(3) (2002), 509–522]. In particular, when 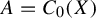$A=C_0(X)$ is commutative, amenability of 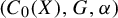$(C_0(X),G,\alpha )$ coincides with topological amenability of the G-space 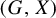$(G,X)$ .

Keywords

dynamical systemscrossed productslocally compact groupsamenable actions

MSC classification

Primary: 46L55: Noncommutative dynamical systems
Secondary: 47L65: Crossed product algebras (analytic crossed products) 46L07: Operator spaces and completely bounded maps
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 8 , August 2022 , pp. 2468 - 2508
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abadie, F., Buss, A. and Ferraro, D.. Amenability and approximation properties for partial actions and Fell bundles. Bull. Braz. Math. Soc., New Series doi: 10.1007/s00574-021-00255-8. Published online 2 May 2021.CrossRefGoogle Scholar
Anantharaman-Delaroche, C.. Action moyennable d’un groupe localement compact sur une algèbre de von Neumann. Math. Scand. 45 (1979), 289–304.CrossRefGoogle Scholar
Anantharaman-Delaroche, C.. Action moyennable d’un groupe localement compact sur une algébre de von Neumann II. Math. Scand. 50 (1982), 251–268.CrossRefGoogle Scholar
Anantharaman-Delaroche, C.. Systèmes dynamiques non commutatifs et moyennabilité. Math. Ann. 279(2) (1987), 297–315.CrossRefGoogle Scholar
Anantharaman-Delaroche, C.. Amenability and exactness for dynamical systems and their ${C}^{\ast }$ -algebras. Trans. Amer. Math. Soc. 354(10) (2002), 4153–4178.CrossRefGoogle Scholar
Anantharaman-Delaroche, C.. On spectral characterizations of amenability. Israel J. Math. 137 (2003), 1–33.CrossRefGoogle Scholar
Anantharaman-Delaroche, C. and Renault, J.. Amenable groupoids (Monographie de l’Enseignement Mathématique, 36). l’Enseignement Mathématique, Genève, 2000.CrossRefGoogle Scholar
Bédos, E. and Conti, R.. On discrete twisted ${C}^{\ast }$ -dynamical systems, Hilbert ${C}^{\ast }$ -modules and regularity. Münster J. Math. 5 (2012), 183–208.Google Scholar
Bédos, E. and Conti, R.. Fourier series and twisted ${C}^{\ast }$ -crossed products . J. Fourier Anal. Appl. 21(1) (2015), 32–75.CrossRefGoogle Scholar
Bédos, E. and Conti, R.. The Fourier–Stieltjes algebra of a ${C}^{\ast }$ -dynamical system. Internat. J. Math. 27(6) (2016), 1650050, 50 pp.CrossRefGoogle Scholar
Blecher, D. P.. On selfdual Hilbert modules. Operator Algebras and Their Applications (Waterloo, ON, 1994/1995) (Fields Institute Communications, 13). Ed. Fillmore, P. A. and Mingo, J. A.. American Mathematical Society, Providence, RI, 1997, pp. 65–80.Google Scholar
Blecher, D. P. and Le Merdy, C.. Operator Algebras and Their Modules—An Operator Space Approach. Oxford University Press, Oxford, 2004.CrossRefGoogle Scholar
Blecher, D. P. and Smith, R. R.. The dual of the Haagerup tensor product. J. Lond. Math. Soc. (2) 45(1) (1992), 126–144.CrossRefGoogle Scholar
Buck, R. C.. Bounded continuous functions on a locally compact space. Michigan Math. J. 5 (1958), 95–104.CrossRefGoogle Scholar
Buss, A., Echterhoff, S. and Willett, R.. Amenability and weak containment for actions of locally compact groups on ${C}^{\ast }$ -algebras. Preprint, 2021, arXiv:2003.03469.Google Scholar
Effros, E. G. and Ruan, Z.-J.. Operator Spaces (London Mathematical Society Monographs, New Series, 23). Clarendon Press, Oxford, 2000.Google Scholar
Effros, E. G. and Ruan, Z.-J.. Operator space tensor products and Hopf convolution algebras. J. Operator Theory 50 (2003), 131–156.Google Scholar
Exel, R.. Amenability for Fell bundles. J. Reine Angew. Math. 492 (1997), 41–73.Google Scholar
Exel, R. and Ng, C.-K.. Approximation property of ${C}^{\ast }$ -algebraic bundles. Math. Proc. Cambridge Philos. Soc. 132(3) (2002), 509–522.CrossRefGoogle Scholar
Eymard, P.. L’algèbre de Fourier d’un groupe localement compact. Bull. Soc. Math. France 92 (1964), 181–236.CrossRefGoogle Scholar
Granirer, E. E. and Leinert, M.. On some topologies which coincide on the unit sphere of the Fourier–Stieltjes algebra $B(G)$ and of the measure algebra $M(G)$ . Rocky Mountain J. Math. 11(3) (1981), 459–472.CrossRefGoogle Scholar
Haagerup, U.. The standard from of von Neumann algebras. Math. Scand. 37 (1975), 271–283.CrossRefGoogle Scholar
Haagerup, U. and Kraus, J.. Approximation properties for group ${C}^{\ast }$ -algebras and group von Neumann algebras. Trans. Amer. Math. Soc. 44(2) (1994), 667–699.Google Scholar
Hamana, M.. Injective envelopes of dynamical systems. Toyama Math. J. 34 (2011), 23–86.Google Scholar
Hewitt, E. and Ross, K. A.. Abstract Harmonic Analysis. Volume 1: Structure of Topological Groups, Integration Theory, Group Representations (Grundlehren der mathematischen Wissenschaften, 115), 2nd edn. Springer-Verlag, New York, 1979.CrossRefGoogle Scholar
Ikunishi, A.. The ${W}^{\ast }$ -dynamical system associated with a ${C}^{\ast }$ -dynamical system, and unbounded derivations. J. Funct. Anal. 79 (1988), 1–8.CrossRefGoogle Scholar
Ionescu-Tulcea, A. and Ionescu-Tulcea, C.. On the lifting property (I). J. Math. Anal. Appl. 3 (1961), 537–546.CrossRefGoogle Scholar
Kelley, J. L.. General Topology (Graduate Textbooks in Mathematics, 27). Springer-Verlag, New York, 1975.Google Scholar
Lance, E. C.. Hilbert ${C}^{\ast }$ -Modules. A Toolkit for Operator Algebraists (London Mathematical Society Lecture Note Series, 210). Cambridge University Press, Cambridge, 1995.Google Scholar
McKee, A., Skalski, A., Todorov, I. G. and Turowska, L.. Positive Herz–Schur multipliers and approximation properties of crossed products. Math. Proc. Cambridge Philos. Soc. 165(3) (2018), 511–532.CrossRefGoogle Scholar
McKee, A., Todorov, I. G. and Turowska, L.. Herz–Schur multipliers of dynamical systems. Adv. Math. 331 (2018), 387–438.CrossRefGoogle Scholar
Ozawa, N. and Suzuki, Y.. On characterizations of amenable ${C}^{\ast }$ -dynamical systems and new examples. Preprint, 2020, arXiv:2011.03420.CrossRefGoogle Scholar
Paschke, W. L.. Inner product modules arising from compact automorphism groups of von Neumann algebras. Trans. Amer. Math. Soc. 224 (1976), 87–102.CrossRefGoogle Scholar
Pedersen, G. K.. ${C}^{\ast }$ -Algebras and Their Automorphism Groups (London Mathematical Society Monographs, 14). Academic Press, London, 1979.Google Scholar
Pier, J.-P.. Amenable Locally Compact Groups (Pure and Applied Mathematics. A Wiley–Interscience Publication). John Wiley & Sons, Inc., New York, 1984.Google Scholar
Ren, L.-B.. Introduction to Operator Algebras. World Scientific Publishing, Singapore, 1992.Google Scholar
Renault, J.. A Groupoid Approach to ${C}^{\ast }$ -Algebras (Lecture Notes in Mathematics, 793). Springer, Berlin, 1980.Google Scholar
Ryan, R. A.. Introduction to Tensor Products of Banach Spaces (Springer Monographs in Mathematics). Springer, London, 2002.CrossRefGoogle Scholar
Sakai, S.. On the reduction theory of von Neumann. Bull. Amer. Math. Soc. 70 (1964), 393–398.CrossRefGoogle Scholar
Suzuki, Y.. Simple equivariant ${C}^{\ast }$ -algebras whose full and reduced crossed products coincide. J. Noncommut. Geom. 13(4) (2019), 1577–1585.CrossRefGoogle Scholar
Takemoto, H.. On the weakly continuous constant field of Hilbert space and its application to the reduction theory of von Neumann algebra. Tohoku Math. J. (2) 28(3) (1976), 479–496.CrossRefGoogle Scholar
Takesaki, M.. Theory of Operator Algebras I (Encyclopaedia of Mathematical Sciences, 124). Springer-Verlag, Berlin, 2003. Reprint of the first (1979) edition.Google Scholar
Takesaki, M.. Theory of Operator Algebras II (Encyclopaedia of Mathematical Sciences, 125). Springer-Verlag, Berlin, 2003.CrossRefGoogle Scholar
Williams, D. P.. Crossed Products of ${C}^{\ast }$ -Algebras (Mathematical Surveys and Monographs, 134). American Mathematical Society, Providence, RI, 2007.Google Scholar
Zettl, H.. A characterization of ternary rings of operators. Adv. Math. 48 (1983), 117–143.CrossRefGoogle Scholar
Zimmer, R. J.. Amenable ergodic group actions and an application to Poisson boundaries of random walks. J. Funct. Anal. 27 (1978), 350–372.CrossRefGoogle Scholar