Article contents
Almost proximal extensions of minimal flows
Published online by Cambridge University Press: 16 January 2023
Abstract
In this paper, we study almost proximal extensions of minimal flows. Let 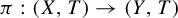 $\pi : (X,T)\rightarrow (Y,T)$ be an extension of minimal flows. Then
$\pi : (X,T)\rightarrow (Y,T)$ be an extension of minimal flows. Then 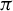 $\pi $ is called an almost proximal extension if there is some
$\pi $ is called an almost proximal extension if there is some 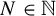 $N\in {\mathbb N}$ such that the cardinality of any almost periodic subset in each fiber is not greater than N. When
$N\in {\mathbb N}$ such that the cardinality of any almost periodic subset in each fiber is not greater than N. When 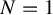 $N=1$,
$N=1$, 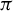 $\pi $ is proximal. We will give the structure of
$\pi $ is proximal. We will give the structure of 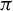 $\pi $ and give a dichotomy theorem: any almost proximal extension of minimal flows is either almost finite to one, or almost all fibers contain an uncountable strongly scrambled subset. Using the category method, Glasner and Weiss showed the existence of proximal but not almost one-to-one extensions [On the construction of minimal skew products. Israel J. Math. 34 (1979), 321–336]. In this paper, we will give explicit such examples, and also examples of almost proximal but not almost finite to one extensions.
$\pi $ and give a dichotomy theorem: any almost proximal extension of minimal flows is either almost finite to one, or almost all fibers contain an uncountable strongly scrambled subset. Using the category method, Glasner and Weiss showed the existence of proximal but not almost one-to-one extensions [On the construction of minimal skew products. Israel J. Math. 34 (1979), 321–336]. In this paper, we will give explicit such examples, and also examples of almost proximal but not almost finite to one extensions.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 1
- Cited by



