INTRODUCTION
Several European countries have systems for timely monitoring of all-cause mortality. However, small but sustained changes in number of deaths may not give rise to signals in these national systems because they are masked by random variations. Pooling data across countries may decrease this variation – in the case of an equal and simultaneous change in excess number of deaths, pooling of data will increase the signal-to-noise ratio with the square-root of the times the number of deaths is increased. Thus, by combining data from several countries, small simultaneous changes in excess mortality may become visible. Pooling data across countries will also increase the power of monitoring mortality in population groups with an expected low number of deaths, e.g. children or fertile women. Furthermore, analyses at country level may not reveal spatial patterns across Europe related to spread of diseases between countries. The European mortality monitoring project (EuroMOMO) has developed a common algorithm which enables the operation of routine public-health mortality-monitoring for detection and measurement of unusual changes in the number of deaths in a timely manner. When possible, these changes are related to public-health threats across Europe. The core of EuroMOMO is country-specific monitoring of the number of death registrations. These national/regional data are analysed at the country level using the program package A-MOMO [Reference Gergonne1]. The algorithm compares the observed number of deaths with an estimated baseline number of expected deaths at the national level. The A-MOMO algorithm applies the Serfling method, with spring and autumn as estimation reference periods [Reference Gergonne1, Reference Serfling2].
Number of deaths from countries with different numbers of inhabitants will not be directly comparable, and timely population figures are not available. However, a standardized score (z score), showing how many standard deviations the observed weekly number of deaths is above or below the national baseline, will be comparable across countries and over time, and can be applied in pooled analyses. The aim of the present study was to examine if pooling of data revealed European mortality patterns that went unnoticed locally. Furthermore, we aimed to provide a routine output describing both national and overall European patterns of mortality and unexpected changes in number of deaths.
Based on the algorithm used and the output provided by the locally run A-MOMO, we present and discuss two approaches for combining data and conducting pooled analyses. We apply the pooled analyses based on weekly reporting to EuroMOMO from 16 participating European countries, to illustrate differences between age groups and patterns of mortality for the 2008/09 to 2010/11 seasons, in particular looking at the influenza A(H1N1)pdm09 pandemic season in 2009/10.
METHODS
Data
Sixteen countries (Table 1) participated by collecting national or regional data on number of weekly death registrations, processing these locally by the A-MOMO program package, and submitting weekly outputs to the EuroMOMO project hub at Statens Serum Institut (SSI), Denmark (Fig. 1). Data received from each country by the EuroMOMO hub were aggregated by week and by age groups (0–4, 5–14, 15–64, ≥65 years, and all ages). Data consisted of the number of registered deaths and the estimated number of deaths adjusted for delay in registration to compensate for deaths not registered yet. Data also contained weekly information on expected number of deaths (baseline), deviation from the baseline (delay adjusted deaths – baseline), as well as the z score expressing the relative deviation from the baseline (see Appendix).

Fig. 1. Weekly procedures at national and European level.
Table 1. Participating countries
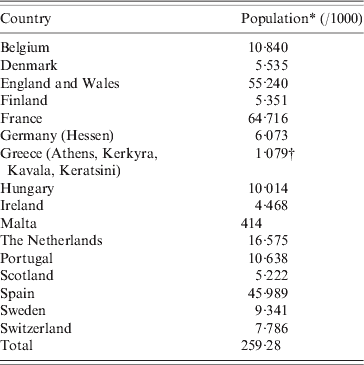
* 1 January 2010.
† 1 January 2001.
Input from the 16 countries was combined and used for the pooled analyses.
Pooling data: methodological considerations
When pooling data the following were considered:
(1) Adjustment for delay in reporting. Since different countries have different delays in the process of registration of deaths and thus in the reporting of deaths, no overall delay-adjustment is possible. Using the delay-adjusted number of deaths from each country creates a local delay-adjusted number of deaths overcoming the challenge of different delays between countries.
(2) Calendar period included in the pooled analyses. Pooled analyses are only feasible for weeks where data from all countries is available simultaneously. Hence, the pooled data available for estimation of a pooled historical baseline will be limited to the period where all countries were able to provide data. This may cause a discrepancy between local baselines and the pooled baseline, as the local baselines will not be based on the same historical calendar interval.
(3) Heterogeneity between countries. Countries may have different patterns of mortality, e.g. larger impact of winter mortality in Northern countries or summer heatwave-associated mortality in the Mediterranean countries. Variation in population structure may also be different. Therefore, mortality may not be homogeneous in pattern (timing of the seasonal peak) and vary in size across countries (amplitude of the seasonal variation).
A straightforward approach for pooling data is to regard all countries as a single ‘country’ by summarizing the weekly number of delay-adjusted deaths from the countries over the calendar period. These data can then be analysed using the same procedures as for each separate country by applying the A-MOMO package, representing one overall ‘country’. This approach is designated the ‘summarized’ approach.
The advantage of the summarized approach is that the same algorithm is applied for estimation of the local baselines and for the pooled baseline. However, a potential discrepancy between the local and the pooled historical baseline [item (2), above] cannot be circumvented using the summarized approach. Item (3) (heterogeneity between countries) is also not addressed because the summarized approach implies that all countries are regarded as one homogeneous country. Furthermore, estimation reference periods may be adjusted to local conditions; i.e. they may not be the same for all countries thereby creating a discrepancy between the estimation reference periods used locally and those used in the summarized approach.
Another approach is to use the locally estimated baselines directly in a country-stratified pooled analysis. This accounts for differences between countries like timing of peaks, historical calendar intervals and estimation reference periods. This method is designated the ‘stratified’ approach. It is done by summarizing both local weekly number of delay-adjusted deaths and expected number of deaths (locally estimated baselines) for all countries. Assuming statistical independence between the countries, the variance of the summarized weekly deviations from the baseline can be calculated directly from the estimated variances of the national deviations (see Appendix).
An advantage of the stratified approach is that the pooled baseline will be a combination of the local baselines. Hence, the stratified approach adjusts for differences in mortality patterns across participating countries, as well as different local historical periods and estimation reference periods. A shortcoming of this approach is the assumed independence between countries. Further, the stratified approach is independent of the locally used algorithms, i.e. the stratified approach can be used also if the countries use different local algorithms to estimate the local baselines.
The two approaches, ‘summarized’ and ‘stratified’, were compared as described below, and the preferred approach used for pooled analyses.
Mortality in the 2008/09 to 2010/11 seasons
We applied the pooled analyses to the period from week 27 (2008) to week 40 (2011). Mortality in this time series is characterized by increased mortality in the winter period, possibly related to several factors including influenza, other seasonal infections and extreme temperatures [Reference Rocklöv, Ebi and Forsberg3]. Cumulated deviation from baseline number of deaths compared to expected number of deaths (baseline) was estimated for each of the seasons (week 27 to week 26 of the following year), as well as for winter (week 40 to week 20 of the following year) and summer periods (weeks 21–39). Age was analysed in groups (0–4, 5–14, 15–64, ≥65 years).
Mortality in season 2009/10 [influenza A(H1N1)pdm09]
A specific objective of the EuroMOMO project was to obtain estimates of mortality associated with the 2009 influenza A(H1N1)pdm09 pandemic [Reference Mazick4]. In the EuroMOMO routine output, weekly excess number of deaths is expressed as the deviation from the expected number of deaths (baseline) over the pandemic season [week 27 (2009) to week 27 (2010)]. This reflects the weekly calendar-time pattern during the season, but not the cumulated excess number of deaths through the season, reflected in the cumulated deviations from the baseline. Cumulated deviation includes any change, both positive and negative, which occurred due to shifts in expected mortality over time. However, the size of the cumulated deviation from the baseline depends on the background population size and does not reveal in itself if the deviation is minor or major. The cumulated deviation relative to the cumulated expected number of deaths quantifies the magnitude of the deviation without the need to calculate specific mortality rates based on the size of the population.
The pooled deviation of mortality from the expected mortality during the H1N1 pandemic was investigated as: (1) the cumulated deviation from the baseline, and (2) the relative cumulated deviation from the baseline relative to the cumulated expected number of deaths. This was done for the total pooled dataset and separately for each pooled age group to reveal differences in the effect of the pandemic between different age groups.
RESULTS
Data
Data from 16 countries (Table 1), locally processed by the A-MOMO package were used, i.e. having different historical estimations periods. Data were reported in week 41 (2011), i.e. including data up to week 40 (2011). In the analyses, we used data up to and including week 26 (2011), thereby excluding the major part of uncertainty due to delay adjustment. Information from all countries was available simultaneously for the consecutive weeks from week 27 (2008) up to and including week 26 (2011), i.e. covering the 2008/09 to 2010/11 seasons.
Method for pooling data
The pooled baseline was estimated using the summarized approach based on the historical period from week 27 (2008) to week 26 (2011) and was different from the pooled baseline using the stratified approach, based on locally estimated baselines using different historical periods (Fig. 2, left panels), both in trend and seasonal amplitude. Hence, the summarized baseline did not correspond to the sum of the local baselines, because it was not estimated on the same historical periods as the locally estimated baselines, but only on the calendar period where all countries provided data. However, the stratified baseline corresponds to the sum of the locally estimated baselines, expanding the amount and time-frame of data used in the local estimations of baselines.

Fig. 2. Comparing the two approaches: summarized (black lines) and stratified (red lines). Green lines = registered; dashed lines = 2 z-score deviation.
If the historical periods used to estimate the local baselines and the local estimation reference periods had been the same for all countries, then the summarized and stratified approach would have been the same (verified in simulation studies; data not show).
As described above the summarized approach did not account for the heterogeneities between local mortality patterns and differences in estimations of baseline. Hence, the stratified approach was preferred.
Pooled analyses
The stratified approach was used to calculate the pooled delay-adjusted and expected number of deaths for all ages (Fig. 3, top panel) and age groups (Fig. 3). Pooled z scores for all ages, together with country-specific z scores, are shown in Figure 4 (bottom panel) and for age groups in Figure 5.

Fig. 3. Pooled analyses for all ages using the stratified approach. Top panel: - - -, daily adjusted; –––, expected (baseline). Bottom panel: –––, Pooled;![]() , countries.
, countries.

Fig. 4. Pooled delay-adjusted (- - -) and expected (–––) number of deaths by age group using the stratified approach.

Fig. 5. Pooled (–––) and country-specific (![]() ) z scores by age group using the stratified approach.
) z scores by age group using the stratified approach.
The pooled z score does not express a ‘mean’ z score, i.e. staying more or less in the middle of the country-specific z scores (Fig. 3, bottom panel). It follows and emphasizes coinciding tendencies in the country-specific z scores; e.g. during the 2008/09 winter season. Over all three seasons, the pooled z score was above 3 in 10% of the weeks, while for single countries it ranged between 1% and 7%. For seasons 2008/09, 2009/10, 2010/11, respectively: pooled 12% countries (0–9%), pooled 9% countries (0–6%), and pooled 8% countries (0–7%).
A graph that shows the pooled z score and country-specific z scores together will depict the pooled signal and indicate if this signal is due to a general trend (all the country-specific z scores will be increased) or due to an increase in some countries only (the country-specific z scores will mainly be around zero, but with increased z scores for the countries with increased mortality).
Age pattern in mortality
Generally, there was a declining trend over calendar period in the number of deaths for persons aged <65 years, and a stable number of deaths for those aged ≥65 years (Fig. 4). There was no recognizable seasonal pattern in the number of deaths in children, but as age increased a seasonal pattern became increasingly prominent. With increasing age, a pattern of increasing excess mortality in the winter season emerged, a pattern also seen in the country-specific analyses (data not shown).
Comparing deviations from the baseline across countries by z scores (Fig. 5) showed an increasing fluctuation with age especially associated with the winter season, but also with summer heatwaves. This pattern was also seen for the nominal excess number of deaths.
Excess mortality in the 2008/09 to 2010/11 seasons
Over the 2008/09 season, the countries saw a total cumulated deviation in mortality from the baseline of 2·7% [95% confidence interval (CI) 2·4–3·0], ranging from 0% to 4% between countries. This deviation was mainly seen in the elderly (Table 2). In the 2009/10 and 2010/11 seasons, the cumulated deviation from the expected number of deaths was lower than in 2008/09, but still significantly higher. Overall, similar patterns were seen in all three winter periods (Table 3). However, in the 2009/10 and 2010/11 pandemic and post-pandemic seasons, increased cumulated deviation from the expected number of deaths was seen mainly in children (aged 5–14 years), but not in the elderly.
Table 2. Seasonal percentage cumulated deviation from the expected number of deaths

CI, Confidence interval.
* Week 27 up to and including week 26 of the following year.
† Adjusted for heterogeneity between countries.
‡ Adjusted for age and heterogeneity between countries.
Table 3. Winter percentage cumulated deviation from the expected number of deaths

CI, Confidence interval.
* Week 40 up to and including week 20 of the following year.
† Adjusted for heterogeneity between countries.
‡ Adjusted for age and heterogeneity between countries.
The summer of 2009 showed no excess number of deaths, but summer 2010 showed a 1·6% (95% CI 1·1–2·1) increase compared to the baseline (Table 4). This increase was mainly in the elderly and was probably associated with the extremely hot summer, especially in southern European countries.
Table 4. Summer percentage deviation from the expected number of deaths

* Week 21 up to and including week 39.
† Adjusted for heterogeneity between countries.
‡ Adjusted for age and heterogeneity between countries.
Mortality in the 2009/10 A(H1N1)pdm09 season
Absolute cumulative, as well as, relative (%) cumulated deviation from the baseline during the 2009/10 influenza A(H1N1)pdm09 season together with the preceding and following season are shown in Figure 6.

Fig. 6. Cumulated deviation from the expected number of deaths. – – – , 2008/09; –––, 2009/10 (pandemic); - - -, 2010/11.
For children aged <5 years, the cumulated deviation during the pandemic increased slightly above the level of mortality in the preceding and following season (during autumn and winter), but ended at the same level as the others at the end of the season.
For children aged 5–14 years, the deviation increased through autumn 2009 to 17% (95% CI 10–24) in week 49 (2009). Then it slowly declined to 7% (95% CI 3–12) at the end of the 2009/10 season. For the 2010/11 season, cumulated deviation from the expected excess summed to the same level as cumulated excess during the 2009/10 season, but the increase was less pronounced and started later in the season.
In the pandemic season, the cumulated deviation from the baseline in the 15–64 years age group was the same as during the preceding and following seasons.
Mortality for persons aged ≥65 years in 2009/10 was below mortality for the preceding season, but the same as for the following season.
As the major part of the observed deaths occurred in the elderly and none of the younger age groups had very high nominal deviations from the baseline, the total deviation over all age groups followed the pattern of the elderly in the previous and preceding seasons.
DISCUSSION
Timely monitoring of mortality is important for public health for many reasons, including the assessment of the impact of severe public-health threats such as epidemics and environmental incidents such as heatwaves. Furthermore, detection of unexplained changes in mortality should be investigated. Existing national mortality surveillance systems are often limited by small numbers of deaths in specific subgroups. Additionally, a variety of national analytical approaches are not suited to detect trends across different countries. To overcome these limitations, we combined data and applied pooled analyses of all-cause mortality across 16 European countries. This approach has an added value because it may reveal changes that may have gone unnoticed in country-specific surveillance, it can provide a picture of the general developments in mortality across Europe, and it may be able to reveal spatial-temporal patterns. Two approaches for combining locally estimated data were investigated. The stratified approach was preferred because it corresponds to the locally estimated baselines, taking into account different historical periods used in the estimation of local baselines and heterogeneity between countries in pattern and variation. A shortcoming of the stratified approach is the assumed independence between countries. Infectious diseases, for example, can spread from country to country where the correlation between bordering countries may be positive, i.e. changing in the same direction. Positive correlation will increase the variance, which again will imply lower z scores. On the other hand, if an illness moves across countries then the number of deaths associated with the illness might be decreasing in the ‘hosting’ country and increasing in the ‘receiving’ country (negative correlation). However, there was no indication of this in our time series, which was limited to three seasons. The correlation may tend to be positive and the assumption about independence implies that the pooled z scores may be slightly overestimated.
The pooled z scores calculated follow the country-specific z scores (Figs 3 and 5) and emphasize simultaneous trends across countries, and can be interpreted as an indicator of overall changes in mortality across countries. However, interpretation should be conducted together with the country-specific z scores because country-specific peaks will reveal if a pooled signal is a general signal or due to a few countries. Pooled analyses will only indicate an overall change in mortality. The cause of this change must be analysed in combination with viruses circulating, environmental factors and/or other factors that may influence all-cause mortality.
The time series of number of deaths and z scores (Figs 4 and 5) shows a high peak in early 2009 consistent with the 2008/09 influenza season, which in Europe was more intense than the previous season and dominated by influenza A(H3N2). Excess deaths were primarily observed in the elderly. By contrast, only modest excess mortality was seen in the 2009/10 season with the influenza A(H1N1)pdm09. There was, however, a small peak in deaths around December/January 2009 in the elderly, and in February 2010 a peak probably associated with a cold snap. Increased mortality primarily in the elderly was observed in summer 2010, coinciding with heatwaves experienced by many European countries.
Estimated baselines of expected deaths showed a declining trend over calendar time in number of deaths for persons aged <65 years, and a stable number of deaths for those aged ≥65 years (Fig. 4). This may be ascribed to the generally ageing populations in many Europe countries, i.e. decreasing number of persons aged <65 years. Assuming the same mortality implies that the number of deaths will decline in the younger age groups.
The z scores for children were mainly stable over calendar time (Fig. 5), i.e. unaffected by seasonal factors affecting mortality in the elderly. For adults and the elderly, a significant seasonal pattern of increased winter mortality emerged with age, probably due to an increasing age-associated vulnerability to influenza and other seasonal illnesses or influences.
Our findings suggest that the 2009/10 influenza A(H1N1)pdm09 pandemic had virtually no effect on overall mortality, especially compared to the preceding and following seasons. An early increased number of deaths were observed in children aged 5–14 years, as has previously been reported [Reference Mazick4]. This is plausible because the A(H1N1)pdm09 virus shares similarities with H1N1 viruses circulating before the 1957 pandemic [5]. Hence, persons in their mid-50 s and above had some cross-immunity and were relatively spared [5, Reference Donaldson6]. Children had no such cross-immunity and vaccination against the pandemic virus in many countries first became available at the peak of the influenza period or just after. Hence, vulnerable children were unprotected at the start and this may be why excess numbers of deaths were observed early in the season. Further, the late availability of vaccines may have reduced the intended vaccination coverage and been the reason for the relatively high child mortality in the following 2010/11 season.
Conclusions and recommendations
We have shown that it is possible to monitor European mortality in pooled analyses based only on number of deaths.
For the pooled analyses to be a useful tool in public-health surveillance, it is important that as many countries as possible participate every week.
Pooled analyses are influenced mostly by countries with the most inhabitants, i.e. having the largest number of deaths. This implies that extreme excess mortality in smaller countries may go unnoticed or that an excess number of deaths in large countries indicates the same for the whole of Europe, even though it is only observed locally. Therefore, it is important that changes in mortality according to the pooled analyses are interpreted in combination with country-specific analyses. Hence, we recommend using the pooled analysis shown in Figure 3, where the pooled z score is supplemented with the country-specific z scores.
Analyses of changes in mortality, country-specific or pooled, indicate changes in mortality, but will not reveal the cause. Hence, the cause of a changes in mortality must be analysed in combination with viruses circulating, environmental factors and others factors that may influence mortality.
Pooled analyses may reveal changes in number of deaths that would have gone unnoticed in separate country analyses. Hence, timely pooled analyses can be a valuable tool in public-health surveillance, especially for smaller or vulnerable groups, like infants, young children or women of fertile age.
ACKNOWLEDGEMENTS
We acknowledge all partners and persons who participated in establishing the local as well as the across-Europe collection of mortality data. This work was supported by the European Commission as part of the EuroMOMO grant (DG SANCO grant 20072001). Neither the European Commission nor any person acting on its behalf is liable for any use made of the information published here.
DECLARATION OF INTEREST
None.
APPENDIX
The pooled weekly delay-adjusted number of deaths is found as the sum of weekly local delay-adjusted (nbc) number of deaths over all countries for each week where all countries have data simultaneously:
Summarized approach
In the summarized approach, the weekly expected number of deaths (baseline) and z scores were estimated using the A-MOMO algorithm [Reference Farrington8] over the historical period where all countries had data simultaneously and using the ‘standard’ weeks for estimation in spring and autumn (spring: 14 ⩽ week ⩽25; autumn: 37 ⩽ week ⩽ 44), i.e. not taking into account potential differences in locally defined estimation periods, nor the different historical periods used locally.
Stratified approach
In the stratified approach the pooled weekly expected number of deaths (baseline) was estimated as the sum of the weekly expected number of deaths (pnb), estimated by the locally run A-MOMO algorithm [Reference Farrington8] over all countries for each week where all countries have data simultaneously. Hence, the estimated baseline is a sum of the country-specific pattern in mortality taking into account the different historical and estimation periods used to estimate the local baselines:
Residual variance and z score
In the local estimations of baselines a 2/3 power transformation was used to account for skewness in the distributions [Reference Gergonne1, Reference Nicoll and McKee7]. Generally, with a power transformation of γ an approximation to the variance of the transformed residuals (nbcγ – pnbγ) was calculated using the delta method: Var(f(X)) ≈ (f(E(X))2 · Var(X):
where E(nbc) = pnb and E(pnb) = pnb. Hence,
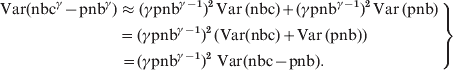 $$\left. \eqalign{{\rm Var}\lpar {\rm nbc}^{\gamma } \minus {\rm pnb}^{\gamma } \rpar \tab \approx \lpar \gamma {\rm pnb}^{\gamma \minus \setnum{1}} \rpar ^{\setnum{2}} \,{\rm Var\, \lpar nbc\rpar } \plus \lpar \gamma {\rm pnb}^{\gamma \minus \setnum{1}} \rpar ^{\rm \setnum{2}}\, {\rm Var\, \lpar pnb\rpar } \cr\tab {\hskip1pt} \equals {\hskip1pt} \lpar \gamma {\rm pnb}^{\gamma \minus \setnum{1}} \rpar ^{\setnum{2}} \, \lpar {\rm Var}\lpar {\rm nbc}\rpar \plus {\rm Var\, \lpar pnb\rpar }\rpar \cr\tab {\hskip1pt} {\hskip1pt}\equals \lpar \gamma {\rm pnb}^{\gamma \minus \setnum{1}} \rpar ^{\setnum{2}} {\rm \ Var}\lpar {\rm nbc} \minus {\rm pnb}\rpar . \cr} \right\}$$
$$\left. \eqalign{{\rm Var}\lpar {\rm nbc}^{\gamma } \minus {\rm pnb}^{\gamma } \rpar \tab \approx \lpar \gamma {\rm pnb}^{\gamma \minus \setnum{1}} \rpar ^{\setnum{2}} \,{\rm Var\, \lpar nbc\rpar } \plus \lpar \gamma {\rm pnb}^{\gamma \minus \setnum{1}} \rpar ^{\rm \setnum{2}}\, {\rm Var\, \lpar pnb\rpar } \cr\tab {\hskip1pt} \equals {\hskip1pt} \lpar \gamma {\rm pnb}^{\gamma \minus \setnum{1}} \rpar ^{\setnum{2}} \, \lpar {\rm Var}\lpar {\rm nbc}\rpar \plus {\rm Var\, \lpar pnb\rpar }\rpar \cr\tab {\hskip1pt} {\hskip1pt}\equals \lpar \gamma {\rm pnb}^{\gamma \minus \setnum{1}} \rpar ^{\setnum{2}} {\rm \ Var}\lpar {\rm nbc} \minus {\rm pnb}\rpar . \cr} \right\}$$Hence the relationship between the residual variance Var(nbc – pnb) and the γ-transformed residual variance will be:
Assuming independence between the pooled countries the pooled residual variance will be:
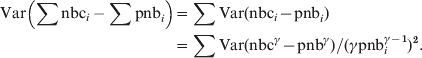 $$\hskip-208pt\eqalign{\displaylines{ {\rm Var}\left( {\sum {{\rm nbc}_{i} -\sum {{\rm pnb}_{i} } } } \right)} \tab\equals \sum {{\rm Var}\lpar {\rm nbc}_{i} \minus {\rm pnb}_{i} \rpar }\hfill\cr \tab {\equals \sum {{\rm Var}\lpar {\rm nbc}^{\gamma } \minus {\rm pnb}^{\gamma } \rpar } \sol \lpar \gamma {\rm pnb}_{i} ^{\gamma \minus \setnum{1}} \rpar ^{\setnum{2}} . \cr}\hfill $$
$$\hskip-208pt\eqalign{\displaylines{ {\rm Var}\left( {\sum {{\rm nbc}_{i} -\sum {{\rm pnb}_{i} } } } \right)} \tab\equals \sum {{\rm Var}\lpar {\rm nbc}_{i} \minus {\rm pnb}_{i} \rpar }\hfill\cr \tab {\equals \sum {{\rm Var}\lpar {\rm nbc}^{\gamma } \minus {\rm pnb}^{\gamma } \rpar } \sol \lpar \gamma {\rm pnb}_{i} ^{\gamma \minus \setnum{1}} \rpar ^{\setnum{2}} . \cr}\hfill $$Using equation (1) with nbc = ∑nbci and pnb = ∑pnbi to have the pooled γ-transformed residual variance:
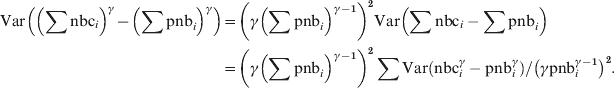 $$\eqalign{{ {\rm Var}\left( \left( \sum {\rm nbc}_{i} \right) }^{\gamma } \minus \left( \sum {\rm pnb}_{i} \right) ^{\gamma } \right)} \tab \equals \left( \gamma \left( \sum {\rm pnb}_{i} \right) ^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} {\rm Var}\left( \sum {\rm nbc}_{i} -\sum {\rm pnb}_{i}\right) \cr \tab \equals\left( \gamma \left( \sum {\rm pnb}_{i} \right) ^{{{\gamma \minus \setnum{1}}} } \right) ^{\setnum{2}} \sum {\rm Var}\left({\rm nbc}_{i} ^{\gamma } -{\rm pnb}_{i} ^{\gamma } \right) \sol \left( \gamma {\rm pnb}_{i} ^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} . \cr}\hfill$$
$$\eqalign{{ {\rm Var}\left( \left( \sum {\rm nbc}_{i} \right) }^{\gamma } \minus \left( \sum {\rm pnb}_{i} \right) ^{\gamma } \right)} \tab \equals \left( \gamma \left( \sum {\rm pnb}_{i} \right) ^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} {\rm Var}\left( \sum {\rm nbc}_{i} -\sum {\rm pnb}_{i}\right) \cr \tab \equals\left( \gamma \left( \sum {\rm pnb}_{i} \right) ^{{{\gamma \minus \setnum{1}}} } \right) ^{\setnum{2}} \sum {\rm Var}\left({\rm nbc}_{i} ^{\gamma } -{\rm pnb}_{i} ^{\gamma } \right) \sol \left( \gamma {\rm pnb}_{i} ^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} . \cr}\hfill$$The local power-transformed residual variances are not included in the A-MOMO output received from the countries, but can be calculated by inverting the formula for the local z score, as this as well as pnb and nbc are included in local data:
The pooled residual variance of the power-transformed deviation from the pooled baseline then becomes:
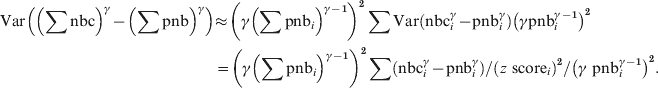 $$\eqalign{{{\rm Var}\left( \left( \sum {\rm nbc}\right) ^{\gamma } \minus \left( \sum {\rm pnb}\right) ^{\gamma } \right)}\tab{\approx{\hskip-1.5pt} \left( \gamma \left( \sum {\rm pnb}_{i} \right) ^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}}\sum {\rm Var}\left({\rm nbc}_{i}^{\gamma } \minus {\rm pnb}_{i}^{\gamma }\right) \left(\gamma {\rm pnb}_{i}^{\gamma \minus \setnum{1}} \right)^{\setnum{2}}} \cr \tab \equals \left( \gamma \left( \sum {\rm pnb}_{i} \right) ^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} \sum \left( {\rm nbc}_{i}^{\gamma } \minus {\rm pnb}_{i}^{\gamma } \right) \sol \left(z{\rm \ score}_{i} \right) ^{\setnum{2}} \sol \left( \gamma {\rm \ pnb}_{i}^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}}.\cr}\hfill $$
$$\eqalign{{{\rm Var}\left( \left( \sum {\rm nbc}\right) ^{\gamma } \minus \left( \sum {\rm pnb}\right) ^{\gamma } \right)}\tab{\approx{\hskip-1.5pt} \left( \gamma \left( \sum {\rm pnb}_{i} \right) ^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}}\sum {\rm Var}\left({\rm nbc}_{i}^{\gamma } \minus {\rm pnb}_{i}^{\gamma }\right) \left(\gamma {\rm pnb}_{i}^{\gamma \minus \setnum{1}} \right)^{\setnum{2}}} \cr \tab \equals \left( \gamma \left( \sum {\rm pnb}_{i} \right) ^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} \sum \left( {\rm nbc}_{i}^{\gamma } \minus {\rm pnb}_{i}^{\gamma } \right) \sol \left(z{\rm \ score}_{i} \right) ^{\setnum{2}} \sol \left( \gamma {\rm \ pnb}_{i}^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}}.\cr}\hfill $$and the pooled z scores become:
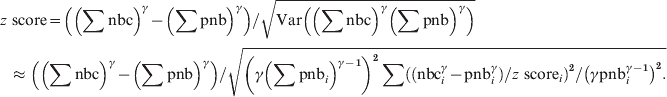 $$\eqalign{{ z{\rm \ score}}\tab \equals \left( \left( \sum {\rm nbc}\right) ^{\gamma } \minus \left( \sum {\rm pnb}\right) ^{\gamma } \right) {\sol} \sqrt{ {\rm Var}\left( \left( \sum {\rm nbc}\right) ^{\gamma } \left( \sum {\rm pnb}\right) ^\gamma\right)}} \cr \tab \!\approx\left( \left( \sum {\rm nbc}\right) ^\gamma \minus \left( \sum {\rm pnb}\right)^\gamma \right) \sol \sqrt{ \left( \gamma \left( \sum {\rm pnb}_{i} \right) ^{{{\gamma \minus \setnum{1}}}} \right) ^{\setnum{2}} \sum \left( \left( {\rm nbc}_{i}^{\gamma } \minus {\rm pnb}_{i}^{\gamma } \right) \sol z{\rm \ score}_{i} \right) ^{\setnum{2}} \sol \left( \gamma {\rm pnb}_{i}^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} .} \cr}\hfill $$
$$\eqalign{{ z{\rm \ score}}\tab \equals \left( \left( \sum {\rm nbc}\right) ^{\gamma } \minus \left( \sum {\rm pnb}\right) ^{\gamma } \right) {\sol} \sqrt{ {\rm Var}\left( \left( \sum {\rm nbc}\right) ^{\gamma } \left( \sum {\rm pnb}\right) ^\gamma\right)}} \cr \tab \!\approx\left( \left( \sum {\rm nbc}\right) ^\gamma \minus \left( \sum {\rm pnb}\right)^\gamma \right) \sol \sqrt{ \left( \gamma \left( \sum {\rm pnb}_{i} \right) ^{{{\gamma \minus \setnum{1}}}} \right) ^{\setnum{2}} \sum \left( \left( {\rm nbc}_{i}^{\gamma } \minus {\rm pnb}_{i}^{\gamma } \right) \sol z{\rm \ score}_{i} \right) ^{\setnum{2}} \sol \left( \gamma {\rm pnb}_{i}^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} .} \cr}\hfill $$The 100*(1 − α) percentage prediction intervals for the pooled weekly baseline ∑pnbi can be calculated by:
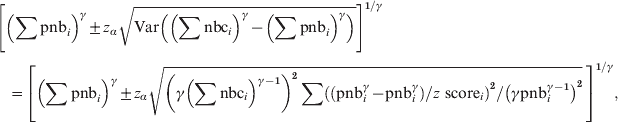 $$\eqalign{\tab\left[ \left( \sum {\rm pnb}_{i} \right) ^{\gamma } \pm z_{\alpha } \sqrt{ {\rm Var}\left( \left( \sum {\rm nbc}_{i}\right) }^{\gamma }\minus \left( \sum {\rm pnb}_{i} \right) ^{\gamma } \right)}\right]^{\setnum{1}\sol \gamma}}} \cr \tab \quad\equals \left[ {\left( \sum {\rm pnb}_{i} \right) ^{\gamma } \pm z_{\alpha } \sqrt {{\left(\gamma {\left( \sum {\rm nbc}_{i} {\rm} \right) }^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} \sum \left( \left( {\rm pnb}_{i} ^{\gamma } \minus {\rm pnb}_{i}^{\gamma } } \right) \sol z{\ \rm score}_{i} \right) ^{\setnum{2}} \sol \left( \gamma {\rm pnb}_{ i}^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} }}}\, \right]^{\setnum{1}\sol \gamma }, \cr}\hfill $$
$$\eqalign{\tab\left[ \left( \sum {\rm pnb}_{i} \right) ^{\gamma } \pm z_{\alpha } \sqrt{ {\rm Var}\left( \left( \sum {\rm nbc}_{i}\right) }^{\gamma }\minus \left( \sum {\rm pnb}_{i} \right) ^{\gamma } \right)}\right]^{\setnum{1}\sol \gamma}}} \cr \tab \quad\equals \left[ {\left( \sum {\rm pnb}_{i} \right) ^{\gamma } \pm z_{\alpha } \sqrt {{\left(\gamma {\left( \sum {\rm nbc}_{i} {\rm} \right) }^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} \sum \left( \left( {\rm pnb}_{i} ^{\gamma } \minus {\rm pnb}_{i}^{\gamma } } \right) \sol z{\ \rm score}_{i} \right) ^{\setnum{2}} \sol \left( \gamma {\rm pnb}_{ i}^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} }}}\, \right]^{\setnum{1}\sol \gamma }, \cr}\hfill $$where zα is the 100*(1 – α/2) percentile of the standard normal distribution.
Cumulated deviation from the baseline
The cumulated deviation from the baseline over W weeks is:
Assuming independence between weeks, i.e. no autocorrelation, then the same methods as used in the stratified analyses can be used. Hence, the γ power-transformed residual variance of the cumulated deviation from the baseline over a calendar period of W weeks can be calculated in the same manner. The 100*(1 – α) percentage confidence interval around the expected deviation from the baseline, which in mean will be 0, will then be:
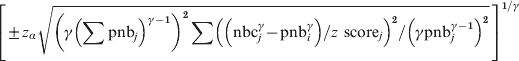 $$\left[ { \pm z_{\alpha } \sqrt {\left( \gamma \left( \sum {\rm pnb}_{j} \right) ^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} \sum \left(\left( {\rm nbc}_{j}^{\gamma } \minus {\rm pnb}_{i}^{\gamma } \right) \sol z{\rm \ score}_{j} \right) ^{\setnum{2}} \sol \left( \gamma {\rm pnb}_{j}^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} } }\, \right]^{\setnum{1}\sol \gamma }\hfill $$
$$\left[ { \pm z_{\alpha } \sqrt {\left( \gamma \left( \sum {\rm pnb}_{j} \right) ^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} \sum \left(\left( {\rm nbc}_{j}^{\gamma } \minus {\rm pnb}_{i}^{\gamma } \right) \sol z{\rm \ score}_{j} \right) ^{\setnum{2}} \sol \left( \gamma {\rm pnb}_{j}^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} } }\, \right]^{\setnum{1}\sol \gamma }\hfill $$and around the observed cumulated deviation from the baseline:
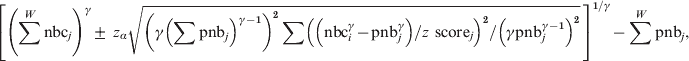 $$\eqalign{\left[ {\left( \sum ^{W} {\rm nbc}_{j} \right) ^{\gamma } \pm {\rm \ }z_{\alpha } \sqrt {\left( \gamma \left( \sum {\rm pnb}_{j} \right) ^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} \sum \left( \left( {\rm nbc}_{i}^{\gamma } \minus {\rm pnb}_{j}^{\gamma } \right) \sol z{\rm \ score}_{j} \right) ^{\setnum{2}} \sol \left( \gamma {\rm pnb}_{j}^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} } }\, \right]^{\setnum{1}\sol \gamma } \minus \sum ^{W} {\rm pnb}_{j} \comma \cr}\hfill $$
$$\eqalign{\left[ {\left( \sum ^{W} {\rm nbc}_{j} \right) ^{\gamma } \pm {\rm \ }z_{\alpha } \sqrt {\left( \gamma \left( \sum {\rm pnb}_{j} \right) ^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} \sum \left( \left( {\rm nbc}_{i}^{\gamma } \minus {\rm pnb}_{j}^{\gamma } \right) \sol z{\rm \ score}_{j} \right) ^{\setnum{2}} \sol \left( \gamma {\rm pnb}_{j}^{\gamma \minus \setnum{1}} \right) ^{\setnum{2}} } }\, \right]^{\setnum{1}\sol \gamma } \minus \sum ^{W} {\rm pnb}_{j} \comma \cr}\hfill $$where ∑W is summing from week 1 to week W and zα is the 100*(1 – α/2) percentile of the standard normal distribution.
Note that the following formulas will both be wrong and give too small confidence intervals (verified in simulations):
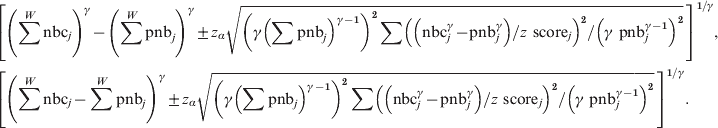 $$\hskip-22pt\eqalign{\tab \left[ {\left( {\sum ^{W} {\rm nbc}_{j} } \right)^{\gamma } \minus \left( {\sum ^{W} {\rm pnb}_{j} } \right)^{\gamma } \pm z_{\alpha } \sqrt {\left( {\gamma \left( {\sum {\rm pnb}_{j} } \right)^{\gamma \minus \setnum{1}} } \right)^{\setnum{2}} \sum \left( {\left( {{\rm nbc}_{j}^{\gamma } \minus {\rm pnb}_{j}^{\gamma } } \right)\sol z{\rm \ score}_{j} } \right)^{\setnum{2}} \sol \left( {\gamma {\rm \ pnb}_{j} ^{\gamma \minus \setnum{1}} } \right)^{\setnum{2}} } } \, \right]^{\setnum{1}\sol \gamma } \comma \cr \tab \left[ {\left( {\sum ^{W} {\rm nbc}_{j} \minus \sum ^{W} {\rm pnb}_{j} } \right)^{\gamma } \pm z_{\alpha } \sqrt {\left( {\gamma \left( {\sum {\rm pnb}_{j} } \right)^{\gamma \minus \setnum{1}} } \right)^{\setnum{2}} \sum \left( {\left( {{\rm nbc}_{j}^{\gamma } \minus {\rm pnb}_{j}^{\gamma } } \right)\sol z{\rm \ score}_{j} } \right)^{\setnum{2}} \sol \left( {\gamma {\rm \ pnb}_{j} ^{\gamma \minus \setnum{1}} } \right)^{\setnum{2}} }}\, \right]^{\setnum{1}\sol \gamma } . \cr} $$
$$\hskip-22pt\eqalign{\tab \left[ {\left( {\sum ^{W} {\rm nbc}_{j} } \right)^{\gamma } \minus \left( {\sum ^{W} {\rm pnb}_{j} } \right)^{\gamma } \pm z_{\alpha } \sqrt {\left( {\gamma \left( {\sum {\rm pnb}_{j} } \right)^{\gamma \minus \setnum{1}} } \right)^{\setnum{2}} \sum \left( {\left( {{\rm nbc}_{j}^{\gamma } \minus {\rm pnb}_{j}^{\gamma } } \right)\sol z{\rm \ score}_{j} } \right)^{\setnum{2}} \sol \left( {\gamma {\rm \ pnb}_{j} ^{\gamma \minus \setnum{1}} } \right)^{\setnum{2}} } } \, \right]^{\setnum{1}\sol \gamma } \comma \cr \tab \left[ {\left( {\sum ^{W} {\rm nbc}_{j} \minus \sum ^{W} {\rm pnb}_{j} } \right)^{\gamma } \pm z_{\alpha } \sqrt {\left( {\gamma \left( {\sum {\rm pnb}_{j} } \right)^{\gamma \minus \setnum{1}} } \right)^{\setnum{2}} \sum \left( {\left( {{\rm nbc}_{j}^{\gamma } \minus {\rm pnb}_{j}^{\gamma } } \right)\sol z{\rm \ score}_{j} } \right)^{\setnum{2}} \sol \left( {\gamma {\rm \ pnb}_{j} ^{\gamma \minus \setnum{1}} } \right)^{\setnum{2}} }}\, \right]^{\setnum{1}\sol \gamma } . \cr} $$In the stratified pooled analyses nbcj and pnbj will be the sums over all countries (nbcj = ∑nbci and pnbj = ∑pnbi) and z scorej the pooled z score.












