Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-05T02:28:41.917Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on the Lag-Phase in the Growth of Micro-Organisms

Published online by Cambridge University Press:  15 May 2009

Arthur Slator
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Ledingham and Penfold have shown that during the lag-phase of growth of B. coli in a nutrient medium the time and bacilli are connected by an equation of the form Xn=K log Y where n and k are constants (the initial seeding = 1). It has been pointed out in this communication that there is a relationship between n and k, and that the above equation can be put in the form

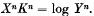
The advantage of this new equation is that K remains of the same value throughout the whole series of experiments.

In the case investigated by Ledingham and Penfold the constant of unrestricted growth is approximately equal to 2K.

The equation can also be put in the form

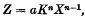
where Z is the “constant” of growth 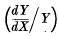at a time X. By suitably adjusting n and a this equation can be made to represent not only the lag-phase of growth but also the logarithmic phase, and the special phase of retarded growth when the X − Y curve is rectilinear. When cell-death occurs the bacteria usually perish at such a rate that the X − Y curve is logarithmic; the general equation therefore also covers this case.

Type
Research Article
Information
Journal of Hygiene , Volume 16 , Issue 1 , July 1917 , pp. 100 - 108
Copyright
Copyright © Cambridge University Press 1917

References

Arrhenius, S. (1915). Quantitative Laws in Biological Chemistry.CrossRefGoogle Scholar
Bayliss, W. M. (1915). Principles of General Physiology.CrossRefGoogle Scholar
Brown, H. T. (1914). Studies on Yeast. Annals of Botany, XXVIII. 197.CrossRefGoogle Scholar
Lane-Claypon, J. E. (1909). Multiplication of Bacteria. Journ. of Hygiene, IX. 239.CrossRefGoogle Scholar
Ledingham, J. C. G. and Penfold, W. J. (1914). Mathematical Analysis of the Lag-phase in bacterial growth. Journ. of Hygiene, XIV. 242.CrossRefGoogle Scholar
Penfold, W. J. (1914). On the Nature of bacterial Lag. Jonrn. of Hygiene, XIV. 215.CrossRefGoogle Scholar
Penfold, W. J. and Norris, P. (1913). The Relation of Concentration of Food Supply to the Generation-time of Bacteria. Journ. of Hygiene, XII. 527.Google Scholar
Slator, A. (1913). The Rate of Fermentation by growing Yeast cells. Biochem. Journ. VII. 197.CrossRefGoogle Scholar
Slator, A. (1916). The Rate of Growth of Bacteria, Trans. Chem. Soc. CIX. 2.CrossRefGoogle Scholar
Sykes, W. J. and Ling, A. R. (1907). The Principles and Practice of Brewing.CrossRefGoogle Scholar