Health service resource needs for pandemic influenza in developing countries: a linked transmission dynamics, interventions and resource demand model

Summary

We used a mathematical model to describe a regional outbreak and extrapolate the underlying health-service resource needs. This model was designed to (i) estimate resource gaps and quantities of resources needed, (ii) show the effect of resource gaps, and (iii) highlight which particular resources should be improved. We ran the model, parameterized with data from the 2009 H1N1v pandemic, for two provinces in Thailand. The predicted number of preventable deaths due to resource shortcomings and the actual resource needs are presented for two provinces and for Thailand as a whole. The model highlights the potentially huge impact of health-system resource availability and of resource gaps on health outcomes during a pandemic and provides a means to indicate where efforts should be concentrated to effectively improve pandemic response programmes.

INTRODUCTION

In recent years substantial progress has been made by many countries to improve their pandemic influenza response plans [1–3]. However, with the current H1N1v pandemic, and sporadic human cases of H5N1 cases still occurring in South East Asia, pandemic preparedness has become an issue of daily public-health policy, testing the operability of strategic response plans. The level of pandemic preparedness has direct impact on the effectiveness of local as well as global disease control. Furthermore, local health services are challenged since they have to provide appropriate treatment, especially to an increasing number of severe influenza cases needing intensive care [4–6]. Developing countries may be particularly taxed by scarce resources in the event of a pandemic since they are often confronted with limited healthcare capacities [7]. Thus, data about resource needs, resource gaps and the best way to improve outbreak response are important to practically support local policy-makers in pandemic planning.

In support of preparedness, simulation exercises have been applied to test operational pandemic response and to evaluate whether resources are sufficient to control disease spread [8–13]. In addition, computer programs exist to estimate the dynamics of a potential pandemic outbreak and to analyse the impact of intervention measures to guide response planning [14, 15]. However, many of these simulation exercises and programs do not explicitly address resource availability or determine the public-health impact of resource gaps. Important questions thus remain as to whether strategic planning is adequate for potential outbreak mitigation or control and about effective options to improve pandemic response, especially in resource-poor settings.

The aim of this study was to develop a simulation model designed for local policy-makers in low- and middle-income countries to estimate the characteristic of a possible pandemic influenza outbreak within a defined population. These results build the basis for calculating the health-system resource needs, for identifying potential resource gaps and for pointing out effective options for improving resource capacities.

METHODS

We developed a mathematical model to describe a pandemic influenza outbreak under different assumptions about resource availability. Feedback loops within the model account for the effect of resource depletion on the expected disease burden and on the expected mortality rate, and to consequently calculate the actual quantities of resources needed. The impacts of the available quantities of antiviral drugs (AVs), vaccines, hospital beds and medical ventilators are considered in the model. To subsequently estimate the quantities of personal protective equipment (PPE) and number of health personnel needed, the model output is linked to per capita resource needs.

For demonstration purpose the model was applied to two provinces in Thailand to answer the following questions: (i) how would a pandemic influenza outbreak progress given the available resources?, (ii) what would be the actual resource required for treating cases according to their disease status?, and (iii) what magnitude of disease burden could be prevented by improving the availability of different resources?

The mathematical model

We used a deterministic SEIR model (Susceptible–Exposed–Infectious–Removed) without age structure assuming a homogeneously mixing population [16]. We extended this baseline model by subdividing the infected population into groups representing differences in clinical severity. We distinguished between asymptomatic cases which are infectious without showing significant symptoms, mild outpatients seeking medical care that can be treated at home, and critical cases in need of hospitalization.

For the model it is assumed that the available quantities of AV treatment courses, hospital beds and medical ventilators have an impact on the number of deaths and the speed of recovery and hence the number of new cases generated during the outbreak. To calculate the effect of AV treatment the two symptomatically infected groups are further subdivided into those receiving AVs and those who do not. Treatment with AVs is assumed to reduce the infectious period and the probability of death. To describe the effects of hospital resource shortcomings the group of critically ill cases is stratified into hospitalized cases (critical cases are assumed to be treated in hospital as long as hospital beds are available, otherwise they become critical outpatients), ventilated cases (critical cases needing mechanical ventilation receive ventilation as long as ventilators are available; cases needing ventilation who do not receiving it will die) and critical outpatients treated at home with and without AV. For these groups different death rates and different infectious periods apply according to their level of disease severity and according to the quality of treatment they receive.

The model allows the effect of additional influenza-relevant intervention measures to be estimated, in particular, hospital interventions (e.g. infection control measures) which reduce transmission within the hospital setting; reduction of contact rates in the community for a defined period of time; and vaccination campaigns that move a proportion of susceptible individuals who are effectively vaccinated to the recovered compartment.

The flow of cases throughout the calculated outbreak is defined by 17 differential equations linking the different model compartments. A simplified compartment flowchart illustrating the overall model structure is given in Figure 1.

Fig. 1. Schematic compartment flowchart of the SEIR model for pandemic influenza transmission. Compartment definition: S, susceptible to influenza infection; E, infected yet not infectious; A, infectious yet not symptomatic; I_a, asymptomatically infectious cases; I_m, mild symptomatic outpatients who seek medical care [not treated with antiviral drugs (AVs)]; I_ma, mild symptomatic outpatients under AV treatment; I_c, critical outpatients not receiving AVs; I_ca, critical outpatients receiving AVs; I_h, critically ill cases treated in hospital, under AV treatment as long as stockpile is sufficient; V, critically ill patients receiving ventilation if available; D, deaths due to influenza complications; R, recovered and immune against infection.

The underlying disease-specific parameters used are based on literature published on pandemic influenza H1N1v. In the model the individual infectivity is set to a fixed parameter. Thus, all cases, regardless of the severity group they belong to, are equally infectious throughout their period of infectivity. However, the duration of infectivity is assumed to vary between different severity groups. These parameters are adjusted according to the model's basic reproduction number (R ₀) (the average number of new cases generated by one infected case, during the time of infectivity in a totally susceptible population, when no intervention measures are in place [17]) in order to be consistent with estimations for the current H1N1 pandemic. Under the parameter values chosen, R ₀ of the simulated outbreak was 1·32 which is in line with currently published values [18, 19].

The model and the linked resource calculator were programmed in MS Excel (Microsoft, USA). A detailed description of the model structure, the model formulae, and the parameter settings used are given in the online Supplementary material.

Health-service resource calculation

Further hospital resource needs are calculated from the model output by linking per capita resource demands with the observed number of cases within the underlying case severity groups. Thus, numbers of hospital personnel needed are calculated from the peak number of observed hospitalized cases in order to estimate the human capacity needed to maintain services during the outbreak peak. For this study it is assumed that the total number of clinical personnel is divided into two day shifts and one night shift. During the day and night shifts on an infectious disease ward, one nurse can care for five and ten cases, and one physician can care for 10 and 40 cases, respectively. For the treatment of ventilated cases it is assumed that during day and night shifts, one nurse can care for one and two patients, respectively, while one physician can care for four cases in either shift. The need for PPE is calculated from the total number of hospitalized cases which occurred throughout the outbreak period in order to estimate the absolute resource quantities needed. Resource depletion per hospital case throughout the hospital stay for surgical masks, N95 respirators and surgical gloves are 30, 10 and 40 per common hospital case and 80, 20 and 100 per ventilated case, respectively. The parameters applied for these depletion rates were based on a review of influenza case records and on interviews with public health professionals in Thailand carried out for a previous resource characterization study [20].

Health-service resource survey

The data used for running the model for the Thai provinces was gathered for a resource characterization survey conducted in summer 2009. For this study questionnaires were sent out to local hospitals, health service providers and local public health authorities at district level to assess the available resource quantities relevant for surveillance, case investigation, case treatment and community containment. Missing data were extrapolated via a two-stage regression model based on population size, provider type, and size of facilities. This analysis was part of a larger study applied across six Asian countries within the AsiaFluCap project (www.asiaflucap.org).

Provinces identified for this analysis

We ran the model for Phichit and Nakhon Si Thammarat provinces in Thailand (Fig. 2) representing two deliberately identified provinces with different demographic and socioeconomic contextual settings and also different levels of health-service resources available to respond to pandemic influenza. Phichit province in lower north Thailand covers an area of about 4500 km² with a population of 554 112 inhabitants. Agriculture is the province's most important economic resource. The gross provincial product (GPP) in 2004 was 2·2 billion Thai Baht (THB) or 45 330 THB (~US$1300) per capita. Nakhon Si Thammarat province in south Thailand has a population of 1 513 163 inhabitants and an area size of about 10 000 km². The province's economy is traditionally based on fishing; however, in recent years the tourism industry has become more important. The province's GPP in 2004 was 9·8 billion THB or 61 000 THB (~US$1800) per capita [21], somewhat higher than that of Phichit province.

Fig. 2. Map showing Phichit and Nakon Si Thammarat provinces in Thailand.

Finally, calculations were performed for all Thai provinces and the results summarized for Thailand as a whole. For these calculations, assumptions based on Thailand's national strategic response plan were made as follows [22]: it was assumed that AVs are used to solely treat critical cases, 20% of hospital beds and ventilators are available for influenza cases, measures for contact reduction decrease the number of daily contacts by 10%, and contact reduction is applied as long as a minimum of 0·5% of the population is symptomatically infected. The latter is based on the assumption that, during periods of high pandemic activity, individuals will change their behaviour to reduce contacts, and/or social distancing measures such as school closure will be implemented. All simulations start with one mild case entering a completely susceptible population.

RESULTS

Running the model in a hypothetical population without any interventions and assuming sufficient hospital resources showed that 31·33% of the population became symptomatically infected over the course of the outbreak. The peak of the outbreak occurred at day 112, when 1·72% of the population were symptomatically infected and 0·026% were hospitalized due to infection. During the course of the outbreak, 0·012% of the population died. Adding contact reduction and AV treatment for critical cases to the described scenario changed the figures as follows: 25·08% of the population became infected over the course of the pandemic, while 0·92% were symptomatically ill and 0·015% were hospitalised at the outbreak peak. In total, 0·006% of the population died due to influenza-related complications, which is a 50% reduction compared to the non-intervention scenario.

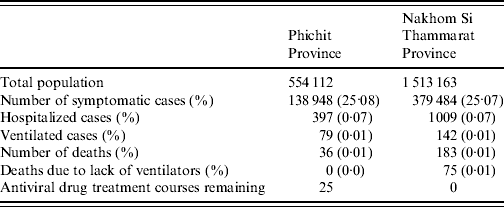
Phichit province has an overall stockpile of 422 antiviral treatment courses, 237 medical ventilators (both adult and paediatric) and 985 available hospital beds. Running the model with these data assuming contact reduction is applied showed that 25·076% of the population were symptomatically infected. The maximum number of observed symptomatic cases at any given time-point was 5096 cases (0·919% of population). During the outbreak period 36 cases died from influenza-related complications. The total outbreak lasted for 188 days. The hospital capacity, including the number of ventilators, as well as the AV stockpile was sufficient to treat all admitted critical cases. However, the remaining amount of 25 AV treatment courses is not sufficient to offer treatment to additional mild cases during the outbreak (Table 1). A graphical representation of the outbreak scenario is given in Figure 3 a.

Fig. 3. Outbreak curve of the calculated pandemic influenza outbreak in (a) Phichit province (n=554 112) and (b) Nakhon Si Thammarat province (n=1 513 163) in Thailand, assuming available resources. The upper graphs show the total number of symptomatic cases stratified by disease subgroups, the lower graphs show the hospitalized subgroups and the cumulative number of deaths, respectively.

Table 1. Modelled pandemic outbreak progression in two Thai provinces taking into account available health-service resources

Assuming sufficient hospital resources, 24 physicians and 64 nurses would be needed per day during the outbreak peak to treat the estimated number of influenza in-patients. The total amount of PPE needed to treat hospitalized cases was estimated to be: 3000 surgical masks, 900 N95 respirators and 3800 surgical gloves for Phichit province.

Nakhon Si Thammarat has an AV stockpile of 518 treatment courses. Furthermore, 99 medical ventilators (both adult and paediatric) and 2642 hospital beds are available in total. Running the model for the province showed that 25·079% of the population became symptomatically infected, with a maximum number of 13 887 cases (0·917% of population) during the outbreak peak. Overall, 183 cases died from influenza-related complications. Although the total outbreak lasted for about 190 days, the model predicted that the AV stockpile would be depleted by day 116. The hospital capacity in terms of beds was sufficient to treat all admitted critical cases. However, there was a shortage of medical ventilators which is associated with 56 excess deaths (excluding those who would die on ventilation anyway). The analysis showed that 27 additional ventilators would be required to offer ventilation to all cases in need. To treat all critically ill patients with AVs, an extra stockpile of 570 courses would be needed. Assuming that resources could be increased to meet these needs, the model predicted that the number of influenza-related deaths could be reduced from 183 to 98; a 54% reduction (Table 1). A graphical representation of the outbreak scenario is given in Figure 3 b.

For the latter outbreak calculation, assuming sufficient resources, 66 physicians and 174 nurses would be needed per day during the outbreak peak to treat all hospitalized influenza cases. The estimated resource needs for hospital PPE would be about 8000 surgical masks, 2400 N95 respirators, and 10 300 surgical gloves.

Running the model for all provinces of Thailand showed that the number of hospital beds was sufficient throughout the country. However, there was a shortage of ventilators and AVs stockpiled for 35 and 40 provinces, respectively, with an associated excess mortality of 579 and 583 deaths resulting from these, respectively. Fifty-one provinces (67·1%) experienced resource gaps in at least one resource and 24 provinces (31·6%) experienced resource gaps in both medical ventilators as well as AVs. The total shortfall in number of ventilators was 318 (range 1–27, mean 9) across the provinces. There was a shortage of 10 744 treatment courses with an average gap of 269 courses (minimum 13, maximum 808) for each province with an AV gap.

DISCUSSION

In order to support policy-making for pandemic preparedness, information about effective and economic ways to improve health-service response is needed. This is especially true for developing countries which are often facing both limited outbreak response capacities as well as limited financial resources to improve pandemic planning. Thus, recommendations about where to invest financial resources for optimum public-health benefits should guide pandemic policy-making. The presented mathematical model provides a means for identifying potential resource gaps as well as high- and low-priority areas for resource allocation and investment based on the disease burden which can be prevented by improving features in health-service response.

The analysis highlights the differences in health outcomes between a province with adequate resources and a province with potential resource gaps. For Phichit province in Thailand, the analysis suggests that the available hospital beds and the number of medical ventilators are adequate for the outbreak scenario simulated by the model. Also the AV stockpile is sufficient to treat all critical cases. However, the surplus does not allow for changing treatment strategies, e.g. by providing AVs to mild outpatients as well. This would reduce both influenza-related complications in cases as well as the total number of cases generated throughout the outbreak. For Nakhon Si Thammarat province the model showed that 56 excess deaths can be prevented by increasing the number of ventilators by 27, which is 27·3% of the number currently available. The AV stockpile must be more than doubled in order to treat all hospitalized influenza cases, which ultimately is predicted to prevent another 29 deaths. Running the model for all provinces in Thailand showed that increasing the number of ventilators and AV treatment courses to sufficient quantities would reduce the number of deaths by 579 and 583, respectively. In both scenarios resources were available to treat critical cases solely, which has almost no effect on preventing the amount of new cases generated throughout the epidemic.

An earlier study on the Thai health system's response to contain a potential H5N1 influenza (bird flu) outbreak indicated that resource gaps already existed during the early phases of a pandemic [20]. However, H5N1 is assumed to be more severe than the currently spreading H1N1 virus causing a higher disease burden and demanding greater health-service capacity. In addition, the earlier study focuses on the ability to contain H5N1 while we study the health-service response to a milder H1N1 scenario.

Our model does not take into account options for modifying or increasing health-service response during the simulated outbreaks since the aim of our study was to identify potential gaps on the basis of the actual resources currently available. However, different options exist to modify responses during an emerging health threat which should be considered in pandemic response planning. In our study only the use of spare capacity of the baseline capacity available for case treatment was analysed. However, improving surge capacity by re-allocating resources from elective non-essential functions or by applying clinical triage guidelines, especially during outbreak peaks, would improve outbreak response capacity during periods of intense resource demand for the large number of patients. Our study highlights the serious effect of shortages in ventilators on the expected number of excess deaths. However, the use of medical ventilators is rarely an elective function, unless it is associated with post-operative recovery, and it can seldom be postponed. One alternative option might be to discontinue medical ventilation for those patients not responding to treatment, in order to provide respiratory support to those who would benefit most [23]. However, such decisions have to follow clear triage guidelines based on bioethical principles to secure equitable and efficient use of scarce resources and to support clinical personnel in decision-making [24, 25].

A further option to improve outbreak response would be the mobilization of resources. The current analysis showed that resources are distributed differently throughout Thailand. In total, 67% of the Thai provinces are facing gaps in availability of medical ventilators or AVs, while others are estimated to have sufficient or even excess health-service resources to deal with the pandemic scenario modelled in our study. This diversity raises important implications in terms of sharing resources for outbreak response across geographical regions. To potentially draw upon capacities from neighbouring regions, the resource availability throughout the country should be analysed to identify geographic clusters of resource gaps and surpluses. Including resource mobilization strategies in national pandemic planning allows the possibility of improving outbreak response without necessarily increasing the quantities of health-service resources.

Since the current model shows resource gaps and the associated excess disease burden, further important questions remain about cost-effective ways to invest in improvement of health-service resources. Apart from the health benefit gained, information about costs associated with resource improvement has to be considered when making decisions about investing in health-service improvement. Hence, information about the financial impact of acquisition, maintenance, and delivery of resources need to be balanced with the disease burden which can be prevented [26].

Due to simplified assumptions of the model and inherent uncertainty surrounding the underlying disease parameter values, the estimated number of cases and deaths as well as the extrapolated resource needs should be interpreted with caution. The model applied here is an extended version of a deterministic SEIR model that assumes a homogeneous mixing pattern within a closed population. Incorporating heterogeneities into the model would allow simulation of a pattern of geographical spread throughout a region or obtaining of age-dependent results to stratify resource needs by age groups. However, the data required for such an analysis would be enormous; data on contact patterns, especially for developing countries, are limited.

Another limitation of the present model is the assumption that all cases are equally infectious regardless of the severity group to which they belong, and that the level of infectivity is constant throughout the infectious period (although duration of infectiousness is assumed to differ between severity classes). Epidemiological studies suggest that, in reality, the degree of infectivity is associated with viral load, which in turn varies with disease severity and time post-infection [18].

The parameters used in our study are taken from the literature. Different parameters for pandemic influenza are published and some of them vary substantially. This is especially the case during early pandemic phases, as with the current H1N1v pandemic, when epidemiological data are limited and of questionable reliability [27]. It has been shown that simple mathematical outbreak models can be useful tools to derive information about outbreak progression when only limited epidemiological data are available [28]. These models rely on few basic parameters which can be simply changed if more recent data become available. Nevertheless, it has to be considered that changes in parameter settings or the accumulation of parameter uncertainties can have a huge impact on the model output with a strong effect on the underlying resource calculations, ranging from sufficient resources to an overwhelmed health system [9].

For the current study, disease- and resource-related parameters were taken from various countries, although most of them were derived from analyses conducted in industrialized societies. However, differences among countries in terms of behavioural, cultural and socioeconomic characteristics, the underlying health of the population, and the quality and accessibility of healthcare services, could influence disease parameter estimates. Furthermore, for some calculations, such as the number of healthcare personnel needed for case treatment, no data were available and the model parameters had to be assumed. However, parameterizing health data for developing countries is a trade-off between what is available and what is needed to conduct a robust analysis [29]. There are many reasons for the underrepresentation of research in developing countries, ranging from poor research capacity to publication bias of journals against so called ‘diseases of poverty’ [30]. This highlights the need to address such imbalances in the availability and quality of data for public-health research and policy-making, and also to find better ways to deal with scarce data in developing countries.

Considering the simple nature of the model and the uncertainty in the parameter settings, the aim of the output is not to provide accurate information on the exact quantities of resources needed. However, the error introduced due to the simplicity of the model acts similarly on all the resource calculations and hence allows a comparative analysis of the effects of resource availability and the consequence of different strategies of resource use. This mathematical model thus represents a means of prioritizing where and how investments should be concentrated in order to improve pandemic response programmes effectively.

CONCLUSION

The current mathematical model is a simple but comprehensive and easy-to-use modelling tool for calculating influenza outbreak progression and the underlying health-service resource demands. It can be applied for pandemic response planning to estimate and compare health-system resource gaps across resource types and geographic areas, and to help prioritize where and which resources should be increased or otherwise improved. This information is especially useful for countries with limited capacity to improve pandemic response as they rely on information to focus efforts on the most relevant resource gaps. The mathematical model can be downloaded from the AsiaFluCap project website at: www.asiaflucap.org.