INTRODUCTION
Estimation of prevalence is a basic requirement in epidemiological studies. Authors usually accompany their observed sample prevalence with a 95% confidence interval (CI) for the population prevalence, to give an impression of the precision of the estimate [Reference Barrio1, Reference Vyse, Hesketh and Pebody2]. In most cases, however, the diagnostic test is imperfect, i.e. it has a sensitivity and/or specificity less than 100% [Reference Aguilar-Setién3, Reference Alonso-Padilla4]. When the sensitivity and specificity of the test are known, the adjusted prevalence, also called true prevalence, is calculated according to the formula
where prev adj, prev obs, Se, and Sp denote adjusted prevalence, observed prevalence (also called apparent prevalence), sensitivity, and specificity, respectively [Reference Rogan and Gladen5, Reference Thrusfield6].
CIs are given in most papers only for the observed prevalence without adjustment for sensitivity and specificity. Usually the simplest asymptotic method, the Wald method is used [Reference Grossman7, Reference Fernández-Limia8], but sometimes Wilson's score method [Reference Garcia-Vazquez9] or the exact Clopper–Pearson method is applied [Reference Moujaber10–Reference Coelho12].
CIs adjusted for sensitivity and specificity are rarely given, although Rogan & Gladen [Reference Rogan and Gladen5] described an appropriate modification of the asymptotic Wald method, which is also included in some textbooks [Reference Thrusfield6], and implemented in some computer programs [13]. In spite of this, some authors calculate CIs naively, adjusting the observed prevalence by the Rogan & Gladen formula, and then calculating a CI using the adjusted prevalence as if that were observed directly, i.e. without the necessary correction in the variance formula [Reference McCluskey14, Reference O'Brien15]. This method results in incorrect CIs, whose actual coverage at a nominal level of 95% can be as low as 60%, even for large samples. The exact Clopper–Pearson CI has been applied with adjustment for sensitivity and specificity in some papers, although infrequently [Reference Thiry16]. The problem regarding exact CIs for the adjusted prevalence is well illustrated by papers applying the exact Clopper–Pearson method for the observed and an asymptotic method for the adjusted prevalence [Reference Bartels17].
Here we apply the approach proposed by Cameron & Baldock [Reference Cameron and Baldock18] to calculate exact two-sided CIs adjusted for sensitivity and specificity. As the Clopper–Pearson method is known to be too conservative for two-sided intervals [Reference Agresti and Coull19, Reference Blaker20], we use Blaker's and Sterne's methods [Reference Blaker20–Reference Reiczigel22] providing shorter exact two-sided CIs.
METHODS
Both Blaker's and Sterne's CIs are derived by inverting the corresponding tests. Therefore we first defined how these tests can be adjusted for sensitivity and specificity. Both of them test for
where p and p hyp denote the unknown true population prevalence and its hypothesized value, respectively.
Assuming H 0 and binomial sampling distribution, the probability that a random sample of size n contains k subjects with the disease (k=0, 1, …, n) is
Given that the sample contains k subjects with the disease, and assuming that the diagnostic procedure has sensitivity Se and specificity Sp, we can calculate the probability that the number of subjects in the sample found to be positive is equal to m (m=0, 1, … , n). The formula for this is as follows:
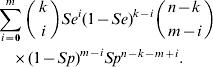
Combining equations (2) and (3), we observe that under H 0 the probability that the number of test positives in the sample is equal to m (m=0, 1, … , n) can be written as
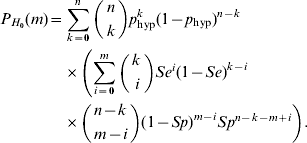
The principle of Sterne's method is that we order the sample space (i.e. the values 0, 1, …, n) according to their probabilities under H 0. From this it follows that the p value belonging to an observed number j of positives in the sample is
where ![]() denotes the probability defined by equation (4). In Blaker's test, we order the sample space according to a so-called acceptability function
denotes the probability defined by equation (4). In Blaker's test, we order the sample space according to a so-called acceptability function
resulting in a p value of
Inversion of these tests results in exact two-sided CIs for prevalence. Test inversion means that observing j positives in the sample, the level 1−α CI runs from the smallest to the largest such p hyp value, for which the test results in a p value ![]() greater than α. Blaker's CI has the advantage that it is always contained in the Clopper–Pearson interval, whereas Sterne's CI, in spite of being slightly more narrow on average than Blaker's CI, may sometimes deliver intervals even wider than the Clopper–Pearson CI.
greater than α. Blaker's CI has the advantage that it is always contained in the Clopper–Pearson interval, whereas Sterne's CI, in spite of being slightly more narrow on average than Blaker's CI, may sometimes deliver intervals even wider than the Clopper–Pearson CI.
It should be noted that the proposed CIs do not have equal error probabilities in the two tails, thus one-sided intervals cannot be calculated from the two-sided ones in the usual way. For an exact one-sided CI the Clopper–Pearson method [Reference Clopper and Pearson23] should be used.
SIMULATION RESULTS
An extensive simulation study was performed to explore the coverage properties of the different methods and to compare the length of resulting 95% CIs. In the simulation we varied sensitivity and specificity 50%, 70%, 90%, 95%, 100%; true population prevalence 1%, 5%, 10%, 30%, 50%, 70%, and sample size 50, 100, 200, 500. From each combination of sensitivity, specificity, prevalence, and sample size, we generated 10 000 random samples and determined 95% CIs by the Wald, Wilson, Clopper–Pearson, Sterne, and Blaker methods. [Detailed results of the simulation study with respect to actual coverage (actual confidence level) and average length can be found on the website of the first author, http://www.univet.hu/users/jreiczig/prevalence-with-se-sp.html.] Simulation with 10 000 replications implies that the standard error of the obtained coverage probabilities is about 0·2%.
The actual coverage of the 95% Wald interval was often <90%, in particular when prevalence was <30%. In the worst cases, with low prevalence (1%), low sensitivity (50%), and high specificity (100%), the coverage was as low as 22·3% (n=50), 38·5% (n=100), 62·6% (n=200), and 85·9% (n=500). The actual coverage of the 95% Wilson interval was considerably better (worst case coverage was 90·8%, 91·5%, 92·1%, 93·9% for n=50, 100, 200, 500, respectively). Similarly to the Wald method, lowest coverage occurred in the case of low prevalence and sensitivity, combined with high specificity.
Exact methods produced in general longer intervals than the Wilson CI. In case of low prevalence, low sensitivity and high specificity the Sterne CI turned out to be even longer than the Clopper–Pearson interval. In these cases, Blaker's CI was the shortest, it was even shorter than the Wilson interval, in spite of the lower coverage of the latter (Table 1). If true prevalence was between 30% and 70%, the Sterne interval was the shortest among exact intervals.
Table 1. Examples in which Blaker's CI proved to be narrower than Wilson's CI while its coverage probability was higher at the same time

EXAMPLE
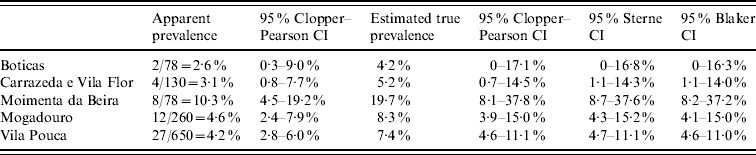
Coelho et al. [Reference Coelho12] conducted a survey to estimate the prevalence of ovine paratuberculosis in sheep flocks in the northeast of Portugal. Presence of antibodies against Mycobacterium avium subspecies paratuberculosis was investigated using a commercial enzyme-linked immunosorbent assay (ELISA) test. According to the manufacturer, the kit has sensitivity between 50% and 65% and specificity >99·5%. These authors [Reference Coelho12] present the seroprevalence values obtained by ELISA for each region, and also give exact Clopper–Pearson CIs for the apparent prevalence. However, they do not correct for test sensitivity and specificity. Table 2 illustrates that exactness of the CI does not prevent bias due to ignoring test imperfectness. The upper confidence limit adjusted for sensitivity and specificity turns out to be twice as high as the unadjusted one. Results without adjustment may lead to over-optimistic estimates of the infection status. Comparing the last three columns of Table 2, it can be seen that the Sterne interval is somewhat (by about 2·5%), and the Blaker interval slightly more (by about 3·5%) shorter than the Clopper–Pearson interval.
Table 2. Seroprevalence estimates of ovine paratuberculosis in sheep in selected regions in Portugal by Coelho et al. [Reference Coelho12]. Seropositivity was determined using an ELISA test with sensitivity and specificity of 50% and 99·5%, respectively
Further examples are available at the first author's website (see Simulation Results section).
DISCUSSION
Here we focused on CI construction, although the proposed methods can also be applied to two-tailed testing, leading to more powerful exact tests. It should be noted that the principles can also be applied to hypergeometric distribution as, i.e. to estimate prevalence in a finite population, adjusted for sensitivity and specificity.
It can be proved that transforming the exact lower and upper confidence limits obtained for apparent prevalence by the Rogan & Gladen formula (1) results in an exact CI for the true prevalence. This leads to an easy implementation of the method. Transformation of asymptotic confidence limits results of course in an asymptotic interval for the true prevalence with coverage comparable to that of the CI for the apparent prevalence. However, the naive method, in which the CI is calculated using the adjusted prevalence as if that value had been actually observed, turns out to be inappropriate. For example, simulating with sensitivity=85%, specificity=90%, and prevalence=3% demonstrates that a 95% two-sided CI constructed in this way has an actual coverage probability of <60%, regardless of whether an asymptotic or an exact CI calculation method is applied.
Computer programs (R functions as well as stand-alone programs for Microsoft Windows) for the described methods are available on the first author's website (see Simulation Results section), together with programs for sample size calculations to the proposed procedures. Note that the Sterne method is also worked out for the difference and ratio of two prevalences from independent samples, including tests and CIs [Reference Reiczigel, Abonyi-Tóth and Singer24]. A future task is to extend this to the case of imperfect tests allowing for different sensitivities and specificities.
How much more narrow the proposed CIs could be than the Clopper–Pearson interval depends on sensitivity, specificity, sample size and true prevalence. According to the simulation results, if true prevalence is between 30% and 70%, Sterne's CI is more narrow than Blaker's CI, whereas for <20% and >80% it is wider. Therefore, if we have prior information about the prevalence, we can choose between the methods. Note that here the expected true population prevalence is meant, not the observed sample prevalence. Choosing the method according to the observed sample prevalence will result in a CI worse than any one of the two methods.
Wilson's score interval, although asymptotic, performed much better than the Wald interval. It can be regarded as appropriate for sample sizes >500. The 92% worst case coverage for samples of ⩽200 cannot be compensated by its length. It was surprising that in some cases Blaker's CI was more narrow on average than Wilson's CI while its coverage was higher at the same time. A few illustrative examples are given in Table 1.
In extreme cases (prevalence=0·01 or 0·02, sensitivity=0·50, specificity=1, n=50), Sterne's CI was longer than the Clopper–Pearson interval. Blaker's CI has the advantage that this cannot occur. As its length never exceeds that of Sterne's CI, and that sometimes it is even narrower than Wilson's asymptotic interval, we propose Blaker's CI for general use.
It should be noted that the proposed methods assume that sensitivity and specificity are known exactly. These values are used in the procedure as fixed numbers known without any uncertainty. If they are estimated from an experiment of comparable size, then the uncertainty in sensitivity and specificity estimates should be accounted for in the CI construction, finally resulting in wider CIs. Rogan & Gladen [Reference Rogan and Gladen5] described how this can be done for the Wald interval, but currently it has not been developed for exact intervals.
CONCLUSION
Estimates of disease prevalence may be seriously biased if sensitivity and specificity of the diagnostic test are disregarded. In case of known sensitivity and specificity CIs are easy to adjust by applying the Rogan & Gladen transformation to the CI endpoints. Since asymptotic methods may not maintain the prescribed confidence level, we propose calculating exact CIs, in particular for sample sizes of ⩽200. Without any prior information on the true population prevalence we propose Blaker's method, as the resulting CI is always contained in the Clopper–Pearson CI. Note that if one-sided exact CIs are needed, the Clopper–Pearson interval is the only available option.
DECLARATION OF INTEREST
None.
ACKNOWLEDGEMENTS
The authors thank the two anonymous referees for their comments that led to a considerable improvement of the paper.




