INTRODUCTION
Foot-and-mouth disease (FMD) is a highly contagious disease of cloven-hoofed animals, which is endemic in many parts of the world. It is of enormous social and economic significance, both in endemic regions and countries which are considered disease-free by the OIE (World Organisation for Animal Health). Trade restrictions resulting from the disease are costly, therefore eradication is a high priority when there is an outbreak in a formerly disease-free country. This involves movement restrictions and the culling of all susceptible animals on infected or high-risk premises. In addition, there is now an acknowledged preference for the use of emergency vaccination in any control strategy [Reference Anderson1, Reference Follett2], and this is reflected in the contingency planning of all European Union (EU) member states [3]. Vaccination is also a primary tool when attempting to suppress the disease or establish disease-free zones in countries with endemic FMD.
Emergency vaccination is applied to induce herd immunity leading to reduced disease (clinical infection) and virus transmission [Reference Orsel4, Reference Orsel5], although the relative level of protection provided by a single dose of vaccine (compared to the immunity developed by animals in endemic countries who are routinely vaccinated) has yet to be determined precisely in the field [Reference Orsel6]. Protection is not immediate and depends on the strength of challenge and the antigenic match of the virus and vaccine. Perhaps most importantly, vaccinated animals may be protected from clinical disease but still become infected [Reference Cox7, Reference Parida8], with the strength of challenge likely to be a significant determinant of whether or not this occurs. In ruminants, the FMD virus (FMDV) is able to persist, at low levels, beyond the periods of acute infection or clinical disease and recovery: where virus is found more than 28 days after the initial infection these animals are termed ‘carriers’. Transmission of infection by carriers has so far not been recorded in domesticated species [Reference Parida9], unlike in wild buffalo [Reference Hedger and Condy10, Reference Dawe11]. However, the significance of carrier animals in the epidemiology of FMD is still not understood [Reference Kitching12], and there is at least a theoretical risk that they could initiate new outbreaks [Reference Barnett and Cox13].
The probability of persistence is particularly important when considering an emergency vaccination-to-live control policy, since this may result in vaccinated and unvaccinated animals coming into contact after disease restrictions are lifted. For a country to regain the benefits of disease-free status it has to provide proof of absence of virus, and EU regulations require that vaccinated animals must be tested prior to the lifting of disease control restrictions [14]. Although it is now possible to distinguish between vaccinated animals and those recovered from infection through infection-specific tests for antibodies against viral non-structural proteins (NSP) [Reference Moonen15], with defined individual sensitivity and specificity [Reference Paton16, Reference Brocchi17], the value and efficacy of testing regimens cannot be determined until the likely prevalence of carriers has been established.
Here, we consider the potential for carrier cattle or sheep to remain undetected following an outbreak, where detection is defined as disease being found and the relevant authority notified. For virus to persist in such a way requires a sequence of events to occur. First, a herd or flock must become infected. Second, there must be a failure to notice this (and then notify the competent authority), so that animals are able to recover instead of being removed (culled). Finally, recovered animals must include at least one carrier for the herd or flock to be considered persistently infected. Assuming that the removal of an infected herd is based on the detection of clinical signs alone, it is possible to calculate the likelihood of detection and assess whether subsequent systematic serological testing is required or feasible. Clinical signs are usually obvious in unprotected cattle, since they almost always develop disease, but are less so in vaccinated animals which may be protected from disease but not from subclinical infection. Sheep may not show obvious signs, with or without vaccination.
Furthermore, whether an animal becomes persistently infected appears to be influenced by vaccination [Reference Cox7, Reference Parida8], but at present it is not possible to predict from which individual animals virus may subsequently be recovered [Reference Parida9].
We are primarily interested in the risk of an animal becoming infected, remaining undetected and subsequently not clearing the virus. It is the potential for carrier herds or flocks to remain undetected that is important rather than the existence of persistently infected animals per se. It is for these groups which have evaded conventional detection that serosurveillance is required, and their likely number will determine whether such a programme is worthwhile. Furthermore, the likely number of carriers in such herds or flocks will determine the test sensitivity and specificity necessary to identify them.
METHODS
We construct a simple probabilistic model for FMDV persistence in a herd or flock based on currently available data, with transmission of the virus and development of the disease all assumed to occur independently within animals. Spread of disease within herds is not considered since recent studies have indicated that ‘most likely no virus transmission will occur within a vaccinated [cattle] herd’ [Reference Orsel6] while ‘virus transmission from vaccinated subclinically infected sheep to introduced vaccinated sentinels is not sufficient to cause NSP seroconversion or significant virus shedding’ [Reference Parida8]. In addition, the exclusion of within-group transmission from the model is justifiable for herds or flocks where individuals have all been challenged at about the same time, or other situations in which there is no significant virus excretion from other individuals during the initial stages of infection – as is expected in vaccinated individuals [Reference Orsel6, Reference Barnett18, Reference Cox19]. The situation modelled here is of naive stock vaccinated prior to the arrival of virus.
Results from transmission experiments provide estimates of the relevant probabilities, while the number of animals challenged on an infected premises (IP) was assumed to be the same as estimated from the 2001 UK outbreak [Reference Arnold20]. A distinction is made between diseased and subclinically infected animals to allow for the effect of clinical detection and the removal (culling) of livestock on IPs to be considered. Variation in effectiveness with respect to time between vaccination and challenge is also made explicit.
Model
The transition of an animal to carrier status can be considered as a number of distinct stages. An animal challenged with virus may either become infected or not. Infected animals may become diseased or remain subclinical. Infected animals may then either completely clear the virus from their system or become carriers (the definition of persistence depends on animals failing to clear virus by a certain time post-challenge – see Experimental Challenge section). The probability of becoming a carrier is different between subclinically infected and diseased animals. The relevant conditional probabilities are shown in Table 1.
Table 1. The conditional probabilities relevant to the persistence of infection in challenged animals
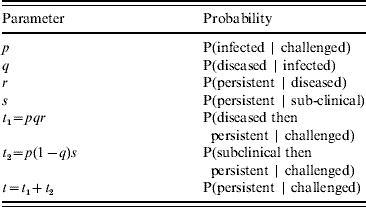
We define Px (a|b) as the binomial probability mass function of a successes out of b trials with individual success probability x, where x is one of the probabilities listed in Table 1. We do not include within-herd transmission and thus assume that each animal changes state independently of any others in the group. The probability of having m undetected carriers in a group of h challenged animals may therefore be written as:

where h is the number of animals challenged, i is the number of challenged animals which become infected, j is the number of infected animals which develop the disease (so i−j is the number of subclinically infected animals), k is the number of diseased animals who become carriers and m−k is the number of subclinically infected animals which become carriers (so that there are m carriers in total). Here Δj is the probability of not detecting j diseased animals (i.e. showing clinical signs) in the herd, which could potentially be dependent on a number of factors in addition to the number of diseased animals j including, most obviously, the herd size n. We would expect this probability to be highly variable, depending upon species, breed and farming practices.
If there is no detection (Δj≡1), equation (1) simplifies to
where t is given the probability of persistence in all challenged animals (as given in Table 1). However, in most cases, it is undetected persistence despite detection that is of interest and so we wish to be able to distinguish between herds which are removed and those which are not, and this requires us to differentiate between animals which were subclinically infected and those which developed disease. This is particularly important as the frequency of persistence differs markedly between diseased and subclinically infected animals, at least in cattle severely challenged within a fortnight of vaccination (see Table 2).
Table 2. Experimental results for cattle used as estimates for the various transition probabilities: here a/b represent a positives out of b subjects.The model functions are fitted to the data independent of vaccine dose (for parameter definitions see Table1)
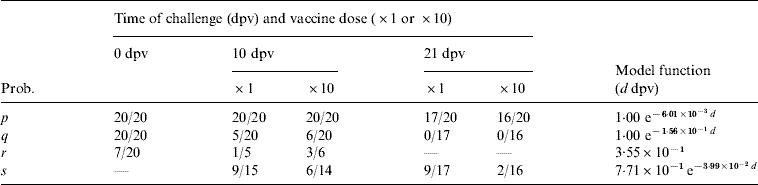
dpv, Days post-vaccination.
For simplicity we consider the case where herds are detected provided at least J animals develop clinical disease. In this case only herds with fewer than J clinical animals can contribute to the number of undetected herds which remain, so that equation (1) becomes:

Finally, we need to consider the number of animals h that we expect to be challenged in a herd or flock of n animals, given that they are on an IP. The probability of m carriers in a challenged group of n animals is given by:
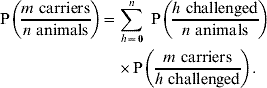
Available epidemiological data suggests that there is high variability in the number of challenged animals in a group [Reference Arnold20]: we therefore define Q k, μ(n)(h) as the (appropriately normalized) negative binomial probability mass function of h cattle being challenged in a herd of n animals, where k is the dispersion parameter and μ=μ(n) is the expected number of challenged animals. Combining equations (3) and (4) with this gives:
![\eqalign{\tab {\rm P}\left( {{{m \ {\rm carriers}} \over {n \ {\rm animals}}}} \right) \equals \sum\limits_{h \equals \setnum{0}}^{n} \ Q_{k\comma \mu \lpar n\rpar } \left( h \right)\left\{ {\sum\limits_{i \equals \setnum{0}}^{h} P_{p} \lpar i\hskip1\vert\hskip1 h\rpar } \right. \cr \tab\quad \times \left. {\left[ {\sum\limits_{j \equals \setnum{0}}^{{\rm min}\left( {i\comma J \minus \setnum{1}} \right)}\!\! P_{q} \lpar j\hskip1\vert\hskip1 i\rpar \left( {\sum\limits_{k \equals \setnum{0}}^{j}\ P_{r} \lpar k\hskip1\vert\hskip1 j\rpar P_{s} \lpar m \minus k\hskip1\vert\hskip1 i \minus j\rpar } \right)} \right]}\! \right\}. \cr}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160921000226230-0381:S0950268809002349:S0950268809002349_eqnU4.gif?pub-status=live)
We are particularly interested in the probability of having one or more carriers, which is given by:

and the expected number of carriers
in a herd of size n.
To evaluate the necessary requirements of any subsequent serological testing, we may calculate the probability of detecting a persistently infected animal in a herd, given that carriers are present. For a test with sensitivity and specificity of S% and 100%, respectively, this is given by:
![\openup2\eqalign{\tab {\rm P\lpar {\rm detection\hskip1\vert\hskip1 present\ in\ herd}\rpar } \equals \sum\limits_{m \equals \setnum{1}}^{n} \big[ {1 \minus \lpar 1 \minus S\rpar ^{m} } \big] \cr \tab\quad \times {{{\rm P}\left( {m{\rm \ carriers\ out\ on\ }n{\rm \ animals}} \right)} \over {1 \minus {\rm P}\left( {{\rm 0\ carriers\ out\ of\ }n{\rm \ animals}} \right)}}. \cr}\hfill](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160921000226230-0381:S0950268809002349:S0950268809002349_eqn5.gif?pub-status=live)
The specificity of such tests is not considered here, since it is assumed that there will be sufficient time and resources to follow up any positive results for confirmation; in addition, there are potential test systems, based on NSP tests, designed to detect carriers in a vaccinated population which have specificities >99% [Reference Paton16].
For infection on a randomly selected UK farm, the probability of detection is given by:
where Pr(n) is the (normalized) national distribution of herd sizes (derived from the 2006 UK Agricultural Survey).
Experimental challenge data
The experimental data used here comes from a number of transmission studies carried out at the Institute for Animal Health, which are described in detail elsewhere [Reference Cox7, Reference Parida8, Reference Cox19, Reference Cox21].
Animals were considered infected if virus was detected by polymerase chain reaction (PCR) or virus isolation (VI) at any time up to 28 days post-challenge: the frequency of sampling in both sheep and cattle in the experiments was high enough, and the sensitivity and specificity of tests good enough, for these results to be considered as a valid measure of infection. Persistence in cattle was based upon virus detection at 28 days (the standard definition of a carrier is virus persistence beyond this point); persistence in sheep was based upon samples taken 35–39 days post-challenge (when the first samples were taken at more than 28 days post-challenge).
In all cases O1 Manisa oil formulated vaccine was used against challenge with O UKG 2001, although it should be noted that the standard dose is different for cattle [Reference Cox7, Reference Cox19, Reference Cox21] and sheep [Reference Parida8].
Disease was determined by clinical signs based on close, expert inspection of animals. In the context of field detection this would be comparable to observation of lactating cattle by experienced farmers. In practice, detection in the field probably spans the full spectrum, with hill sheep, for example, best considered as completely unchecked. In addition, sheep are often subclinically or only mildly affected anyway [Reference Parida8].
Cattle
Probabilities for infection, protection from disease and persistence of virus in cattle are given by [Reference Cox7, Reference Cox19, Reference Cox21], which provide details of four groups of 20 cattle that received a high-level direct-contact challenge from five infected cattle at: 21 days after a standard vaccination dose; 21 days after a tenfold antigen payload vaccination dose; 10 days after a standard vaccination dose; 10 days after a tenfold antigen payload vaccination dose; in addition, there were 20 unvaccinated control animals. The probability of outcomes as a function of vaccine dose and the number of days post-vaccination (dpv) at which challenge occurred is given in Table 2.
A simple two-parameter exponential curve was used to describe those probabilities which change significantly with time (dpv), with the parameters estimated using maximum-likelihood methods assuming binomial errors (Table 2). Those probabilities which did not change significantly (P>0·05) with respect to dpv (as judged by Fisher's exact tests) were assumed to be constant.
Sheep
The probability of sheep being in various states at different times post-challenge are given by Parida et al. [Reference Parida8] for two groups of sheep vaccinated 4 or 10 days prior to challenge, respectively, and an unvaccinated control group, all of which were challenged by aerosol from FMDV-infected pigs. Curves were again fitted to the data where appropriate (see Cattle section). However, only the probability of an infected animal developing disease (q) changed significantly (P<0·05) with dpv and, in practice, this term dominates the probability and frequency of carriers in sheep; the remaining probabilities were treated as constant (Table 3).
Table 3. Experimental results for sheep used as estimates for the various transition probabilities: here a/b represent a positives out of b subjects (for parameter definitions see Table1)

dpv, Days post-vaccination.
Epidemiological field data
There is likely to be considerable variability in the number of challenged cattle within a herd or the number of challenged sheep within flocks. Based on data for the UK 2001 outbreak (primarily veterinary reports of lesion ageing done by clinical inspection), Arnold and others [Reference Arnold20], estimated that the initial number of infections ranged from one to 113 cattle in herds of <350 cattle, while for sheep the corresponding estimates for the number of initial infections ranged from 1 to 800 per flock (out of 1800) animals.
To reflect this variability, we fitted a negative binomial distribution, with mean dependent on herd size, to these data (which were principally based upon clinical inspection of animals). The maximum-likelihood estimates for the model parameters yielded a mean of μ=4·21+3·86×10−3n, where n is herd size, and a dispersion parameter of k=1·12 (cf. [Reference Arnold20]).
Since experiments suggest that unvaccinated cattle which are challenged always become infected and diseased, for severe challenges at least (see Table 2), it is reasonable to consider the number of initially infected animals as being about the same as this number initially challenged.
In principle, a similar estimate could be made for sheep flocks. However, the greater variations in stocking densities, make it unclear how appropriate it would be to calculate a mean number of initial infections and we therefore consider persistence in challenged sheep only.
RESULTS
Initially, we consider persistence in challenged cattle and sheep (independent of herd or flock size) to allow for the uncertainties inherent in the epidemiological field data. We then consider results for a randomly selected cattle farm in the UK, assuming a negative binomial distribution for the number of challenged animals on an IP, as estimated from the UK 2001 outbreak. Finally, we examine the implications of these results for post-outbreak serosurveillance.
Persistence amongst challenged cattle
In the absence of any detection of clinical signs and subsequent culling, the probability that a challenged bovine becomes a carrier is given directly by t (Table 1):

This gives an individual probability of persistence as 36% for unvaccinated cattle, rising to 49% if challenge occurs 6 dpv and eventually dropping to 20% for challenge at 30 dpv. These values are of the same order as the previously estimated probability of persistence of 50% [Reference Kitching22]. In this case, the probability of at least one carrier animal and the expected number of carriers in a herd of size n are approximated by:

where t is defined by equation (7).
Figure 1 shows the probability of a herd on an (undetected) IP harbouring at least one carrier animal and the expected number of carriers in such a herd, as a function of the number of animals challenged and the time post-vaccination that challenge occurred. A comparison is presented for the case in the absence of detection and where herds are removed if five, two or one or more animals show clinical signs, with the latter case representing excellent detection. Changes in outcome in response to vaccination time are not monotonic, because vaccination protects from infection, but also suppresses (detectable) clinical signs in those animals which do become infected.

Fig. 1. Expected outcome for strongly challenged cattle plotted as a function of the number of animals challenged and the number of days post-vaccination that the challenge occurred. Top panels: The probability of such a herd remaining undetected and containing carrier animals; Bottom panels: The expected percentage of animals in the herd in which virus persists (for herds where no detection occurs and where herds are removed if at least a certain number of animals shows any clinical signs of disease).
The probability of undetected carrier herds is reduced if there is good detection of any clinical signs (i.e. detection of disease even if present in only a small number of animals within the herd and with such herds subsequently removed; i.e. culled). However, the effect of vaccination can reduce this benefit: although vaccination significantly reduces the probability of disease in infected animals (by 99% in the first 30 days), the reduction in the probability of infection in challenged animals is less (a drop of <17% over the same period); thus vaccination initially results in an increase in subclinical infection, which means fewer herds are detected and removed. Furthermore, the probability of persistence in infected animals with disease is lower than for subclinically infected animals (there is a delay of 20 days before the effect of vaccination results in this being reversed). There is an eventual beneficial impact of vaccination on the probability of persistence, but only if vaccination occurred a significant time before challenge, with the interval required becoming longer the more animals are challenged in a herd (Fig. 1).
Because the probability of persistence for individual cattle is high a large proportion of the herd become carriers, and where a reasonable number of animals have been challenged it is almost certain that virus will persist in at least one bovine unless there is good detection (Fig. 1).
Persistence amongst challenged sheep
In sheep, clinical detection is less likely than in cattle [Reference Alexandersen23]; thus, the case in which there is no clinical detection is likely to represent the norm. In this case, for challenge occurring d dpv the probability of persistence in an individual sheep (see Table 1) is given by
and the probability of at least one carrier in a flock and the expected number of carriers is approximated by equation (8).
In sheep, vaccination only impacts on the probability of disease, not any of the other probabilities in the model (Table 3) and, furthermore, the probability of disease decreases rapidly after vaccination. Consequently, the detection and removal of infected flocks has little effect on carrier numbers, since animals do not show clinical signs, preventing infected flocks from being identified (Fig. 2). The benefit of vaccination with regard to reducing carrier numbers is therefore less ambiguous in sheep than in cattle, with the probability of an individual animal becoming persistently infected as a result of being challenged quickly dropping from 31% to near zero. However, in a large group of animals that have all been challenged, the chance of having at least one carrier in the flock remains high: 15%, 56% and 80% for 10, 50 and 100 sheep, respectively.
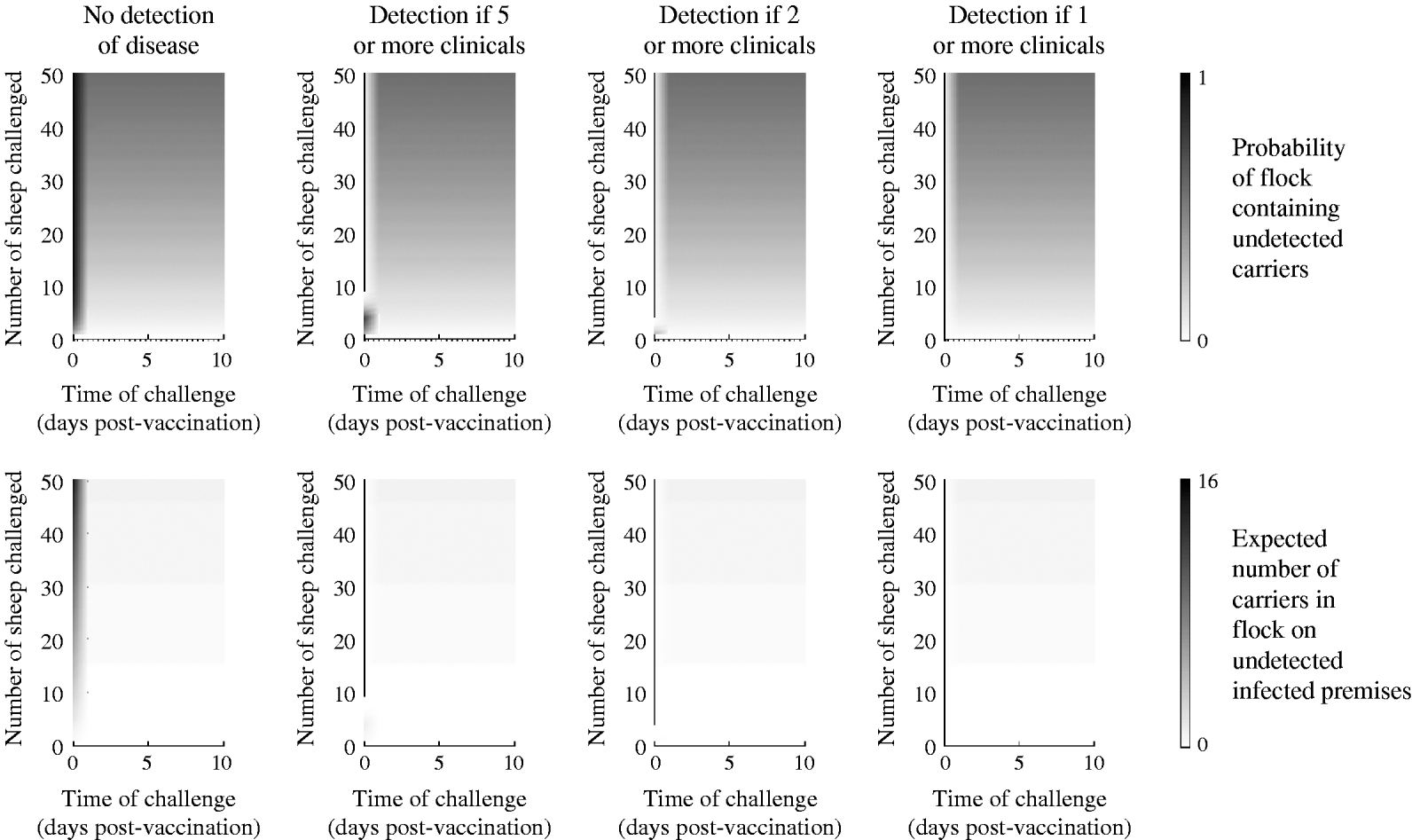
Fig. 2. Expected outcome for strongly challenged sheep plotted as a function of the number of animals challenged and the number of days post-vaccination (dpv) that the challenge occurred. Top panels: The probability of such a flock remaining undetected and containing carrier animals. Bottom panels: the expected percentage of animals in the flock in which virus persists (for flocks where no detection occurs and where flocks are removed if at least a certain number of animals shows any clinical signs of disease). Note the shorter timescale than for cattle in Figure 1.
Persistence in infected cattle herds
Figure 3 shows the probability of persistence and the expected number of carriers in a randomly selected UK cattle herd, once it has been infected. Values were calculated for all UK holding sizes and include estimates for the number of cattle on an IP that are initially challenged based on the mean number of initial infections in the UK 2001 outbreak. The expected outcomes were then calculated by weighting results according to the size distribution of holdings registered in the 2006 UK Agricultural Survey. The predicted low number of expected carriers is predominantly due to the low number of initial infections: only four or five are expected on an average-sized farm (μ=4·6±4·8 for n=103) (see Discussion).

Fig. 3. Expected outcomes for a randomly selected UK cattle herd, which has become infected. Top panel: The probability of such a herd remaining undetected and containing carrier animals. Bottom panel: The expected number of animals in the herd in which virus persists. Vaccination is beneficial when diseased herds are not removed (solid line) but increase persistence, initially at least, if there is successful detection of any clinical signs which occur (broken lines). Here the probabilities for different sized farms have been weighted by data on all holdings with cattle (dairy, beef, mixed, hobby, etc.) from the 2006 UK Agricultural Survey to give results for a randomly selected UK farm; the result for a median-sized (n=61) or mean-sized (n=103) herd are slightly lower, although results for all but the largest holdings are very similar.
Emergency vaccination increases both the probability of persistence and the expected number of carriers in infected herds, compared with the case where animals remain unvaccinated, especially if challenge occurs within 15 days of vaccination. The impact of vaccination on detection also results in an increase in the probability of undetected carrier herds: if clinical signs are always spotted as soon as any animal develops the disease, then there should be a negligible probability of an undetected carrier persisting in an unvaccinated herd since infected animals almost always develop symptoms. Although vaccination may increase the risk of an IP remaining undetected and going on to become a carrier herd, it should be remembered that it can reduce the number of premises which become IPs in the first place (see Discussion).
The confidence in any subsequent surveillance programme detecting carriers in an individual herd is given by equation (5). The results for a randomly selected UK herd are derived by weighting results according to the distribution of herd sizes in the UK, but are similar to results for a median-sized (n=61) or mean-sized (n=103) herd. In the absence of any prior removal of herds showing clinical signs the detection of persistent infection with 95% confidence requires a serological test with a sensitivity of 89% for unvaccinated animals, rising to 92% for cattle challenged 30 dpv, assuming all animals in the herd are tested. Only with tests substantially better than this would it be possible to carry out surveillance which sampled less than the whole herd.
DISCUSSION
Until transmission by recovered but persistently infected animals can be ruled out, the possibility of undetected FMDV carriers is an important issue, especially in disease-free settings. Results from transmission experiments [Reference Cox7, Reference Parida8, Reference Cox19, Reference Cox21], as considered here, offer an insight into the probability of virus persistence occurring. Determining the risk of carrier herds or flocks – groups of animals containing persistently infected individuals which are not detected and removed by conventional means – is important in establishing whether post-outbreak serosurveillance is necessary and practical. Establishing the likely number of persistently infected animals in any such group is also important for designing an appropriate test regimen for determining freedom from disease.
The number of persistently infected animals in a group is predominantly determined by the number of animals initially infected on a premises: this is especially true for vaccinated animals where there is assumed to be little within-herd transmission in cattle [Reference Orsel6], if not pigs [Reference Orsel24]. Results from both the 2001 [Reference Anderson1] and 2007 [25, Reference Ryan26] outbreaks in the UK suggest a great deal of variability in the number of initial infections. Estimates of this number from on-farm lesion ageing must be treated with caution since the oldest infection could easily have been missed in herds with a low number of initially infected animals giving rise to misclassification of multiple second-generation infections as initially infected animals [Reference Ryan26, Reference Henderson27]. Conversely, where disease was recognized early but inspection prior to culling was not thorough, the extent of initial infections might have been underestimated. We have therefore been careful to provide results both for challenged groups alone as well as those based on estimates of the number of animals actually challenged in the field. Ultimately, any confidence we have in predictions of carrier numbers, based upon models of between-farm transmission and possibly incorporating vaccination, is limited by our confidence in estimating initial herd challenge. However, it is useful to note, that our results predict that for cattle herds detection of disease will always be more important in preventing persistence than vaccination (Fig. 1), while the converse is true for sheep flocks (Fig. 2).
The expected number of persistently infected cattle on randomly selected UK premises which have been infected is <2·5 (Fig. 3). Such a low prevalence means that even if all animals were tested, serosurveillance would need to have a sensitivity of at least 89–92% in order to detect infection with 95% confidence, in the absence of any other form of detection. Indeed the sensitivity would need to be even higher if it is assumed that there is good detection of clinical signs (since this results in the prior removal of proportionally more herds with more numerous cases). However, given the high variability in the number of animals challenged it seems likely that serosurveillance with a less sensitive test would still be worthwhile since it would certainly detect some, if not all, IPs and provides an insurance against poor clinical detection. It is also worth noting that although the expected number of carriers is low, the probability of any infected herd (which is not detected) containing at least one carrier remains high (Fig. 3). As well as carriers, continuing virus circulation may also be of concern (especially in endemic settings), i.e. the possible transmission via symptomless (or simply undetected) infected animals, as opposed to recovered ones, something which would further justify the use of serosurveillance.
In herds or flocks with a high number of initially challenged animals there is potentially a greater level of persistence (up to ~50% in cattle and 30% in sheep). In cattle, protection from disease is achieved more rapidly than protection from infection, resulting in a potential increase in carrier numbers as a result of vaccination if challenge occurs shortly after inoculation. In sheep protection from infection is achieved quickly and so this is not an issue.
Whether IPs remain undetected and subsequently result in undetected carrier herds or flocks is predominantly determined by the quality of inspection (in the absence of serosurveillance it is detection alone which is used to remove IPs and thus eliminate carriers). In stock which are checked regularly and thoroughly, the application of vaccination results in an increase in undetected carriers. Where clinical recognition of infection is always difficult (e.g. for sheep), the benefits of vaccination are clear, while for cattle the expected number of persistently infected animals on undetected premises is reduced only if vaccination is applied at least 2 weeks prior to challenge.
Here, we have modelled results derived from expert clinical inspection of experimental animals following high-level challenge: in the field we would expect clinical signs, animal contact and expertise in clinical recognition of disease to all be lower, thus potentially increasing persistence. Other factors may also influence the level of detection, such as an owner identifying disease but failing to notify the authorities.
When applying results it is important to consider cattle and sheep separately, since they differ both in their husbandry (especially the expected level of human contact) and in their response to infection (the expected probability and severity of clinical signs).
Data for other animal species and virus strains are available (see, e.g. [Reference Orsel6, Reference Eble28] or [20, and references therein]) from which transition probabilities and model functions could be derived. However, the broad conclusion reached in this paper would remain unchanged had alternative data been used, due to the dominance of parameters related to initial infection and detection (as opposed to individual animal dynamics) in determining results. The exception would be if it could be shown that vaccination reduces persistence in subclinically infected sheep [Reference Barnett18], something which the data presented here does not support. To apply the model in other settings would require, in addition to transmission experiment results, data on the number of initial infections (and the distribution of herd sizes, for estimates of persistence nationally) equivalent to that used here for the UK. Finally, we note that the above analysis has focused on the likely effects of vaccination on persistence in individual herds and flocks. On an epidemic scale, vaccination will decrease transmission from IPs through reduced excretion and infectivity, which has been shown in sheep [Reference Orsel5], cattle [Reference Barnett18, Reference Cox19] and pigs [Reference Parida29], as well as increasing protection for as yet uninfected premises (see e.g. [Reference Cox21, Reference Eble28]). These effects of vaccination are likely to reduce both the strength of challenge received on a premises and the number of new IPs. While the latter will reduce the possible number of premises which might harbour persistently infected animals, the former may result in less severe disease on those premises where infection does occur, resulting in a potential increase in undetected carriers.
ACKNOWLEDGEMENTS
This work was supported by the Biotechnology and Biological Sciences Research Council (IAH 1320); the Department for the Environment, Food and Rural Affairs (SE2812, SE1122) and the FMD Improcon project of the EU 6th Framework Programme (SSPE-CT-2003-503603). David Paton is a Jenner Research Fellow.
DECLARATION OF INTEREST
None.








