Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T09:47:24.866Z Has data issue: false hasContentIssue false
  • English
  • Français

Assessing the effects of temperature on dengue transmission

Published online by Cambridge University Press:  04 February 2009

H. M. YANG ,
M. L. G. MACORIS ,
K. C. GALVANI ,
M. T. M. ANDRIGHETTI  and
D. M. V. WANDERLEY
H. M. YANG*
Affiliation:
UNICAMP – IMECC, Departamento de Matemática Aplicada, Campinas, SP, Brazil
M. L. G. MACORIS
Affiliation:
SUCEN, Avenida Santo Antonio, Bairro Somenzari, Marìlia, SP, Brazil
K. C. GALVANI
Affiliation:
SUCEN, Avenida Santo Antonio, Bairro Somenzari, Marìlia, SP, Brazil
M. T. M. ANDRIGHETTI
Affiliation:
SUCEN, Avenida Santo Antonio, Bairro Somenzari, Marìlia, SP, Brazil
D. M. V. WANDERLEY
Affiliation:
SUCEN, Avenida Santo Antonio, Bairro Somenzari, Marìlia, SP, Brazil
*
*Author for correspondence: Prof. H. M. Yang, UNICAMP – IMECC, Departamento de Matemática Aplicada, Caixa Postal 6065, CEP 13083-859, Campinas, SP, Brazil. (Email: [email protected])
Rights & Permissions [Opens in a new window]

Summary

The incidence of dengue infection, a vector-borne disease transmitted by the mosquito Aedes aegypti, shows clear dependence on seasonal variation. Based on the quantification method that furnishes the size of the A. aegypti population in terms of the estimated entomological parameters for different temperatures, we assessed the risk of dengue outbreaks. The persistence and severity of epidemics can be assessed by the basic reproduction number R0, which varies with temperature. The expression for R0 obtained from ‘true’ and ‘pseudo’ mass action laws for dengue infection is discussed.

Keywords

Basic reproduction numberglobal warmingmass action lawmathematical modellingrisk of dengue with temperature
Type
Original Papers
Information
Epidemiology & Infection , Volume 137 , Issue 8 , August 2009 , pp. 1179 - 1187
Copyright
Copyright © 2009 Cambridge University Press

INTRODUCTION

Dengue virus, a flavivirus transmitted by arthropods of the genus Aedes, is prevalent in different parts of the world. As a result of being pathogenic for humans and capable of transmission in heavily populated areas, dengue virus (arbovirus) can cause widespread and serious epidemics, which constitutes one of the major public health problems in many tropical and subtropical regions of the world where Aedes aegypti and other suitable mosquito vectors are present.

The epidemiological cycle occurs as follows. Female mosquitoes become infected during the bloodmeal from infectious individuals (the viraemic period) and they then transmit the infection during the next 7–14 days [Reference Mandell, Bennett and Dolin1]. The infection in mosquitoes induces a low level of immunity [Reference Tripet, Aboagye-Antwi and Hurd2] and it is believed, that they probably transmit the virus throughout their lifespan. An infectious mosquito can transmit the virus to a susceptible host during biting and feeding. When an infectious mosquito infects a susceptible host with dengue virus during the bloodmeal, dengue disease can evolve from asymptomatic or classical dengue fever to haemorrhagic dengue, in an average of 4–6 days, which can lead to the death of the host. Manifestation of symptoms varies between 3 and 7 days [Reference Veronesi3], and the virus circulates in the blood typically for 5 days [Reference Mandell, Bennett and Dolin1]. Thereafter, the recovered individual develops lifelong specific immunity against the disease. The prevention against dengue disease is restricted to the controlling mechanisms applied to the vector, because immunization by vaccine remains unavailable.

The extrinsic incubation period of dengue virus in female mosquitoes is large compared to their survival time, which strongly depends on temperature [Reference Nelson4]. For example, both extrinsic and survival time of female mosquitoes are quite similar during winter (low temperature); however, survival is quasi-fivefold higher than the extrinsic period during hot seasons. However, temperature also impacts on all other entomological parameters regarding the mosquito's life-cycle [Reference Rueda5], and, as a consequence, the number of female mosquitoes varies according to seasonal variations. During favourable periods when the size of the mosquito population increases, the risk of dengue infection in humans also increases.

In order to prevent dengue outbreaks, periodic surveys designed to detect changes in key adult indices are important since they allow the detection of adult population fluctuations, which may prompt changes in vector control strategy. In this paper we develop a mathematical model aimed at assessing dengue transmission, taking into account the dependence on temperature of the A. aegypti population size. In order to achieve this task we consider the entomological parameters estimated in our companion paper [Reference Yang6] and use these in a simple mathematical model presented here. There are many mathematical models concerning the treatment of different aspects of dengue epidemics (e.g. [Reference Esteva and Vargas7–Reference Newton and Reiter10]).

The paper is structured as follows. Next, simple deterministic models describing dengue transmission are presented. The following section presents dengue transmission dynamics taking into account the temperature-dependent entomological parameters. In the final section we discuss the results and present conclusions.

MODELLING DYNAMICS OF DENGUE TRANSMISSION

The incidence of dengue disease clearly shows seasonal variation. In wet and humid periods, the transmission of dengue virus is extremely high in comparison with periods of low temperature. To some extent, the intrinsic incubation and infectious periods of dengue virus vary insignificantly with temperature, because the activities of the virus occur inside the human body; nevertheless, the same is not true for mosquitoes (see, e.g. [Reference Lindsay and Birley11] for the duration of the sporogonic cycle at different ambient temperatures). However, in the present study we assume that the extrinsic incubation period is independent of temperature, in order to restrict the risk factor (or sentinel) of dengue outbreaks to the size of the female adult mosquito population. Because entomological parameters of A. aegypti vary broadly with temperature, the size of the mosquito population is strongly affected by temperature.

Dengue virus circulates due to the interaction between human and mosquito populations in urban areas. For this reason the dynamics of dengue transmission must take into account the role played by these populations. Abiotic influences like temperature are encompassed in the model's parameters.

The dynamics of A. aegypti encompassing egg phase, two successive aquatic phases (larval and pupal) and one adult form is reported in a companion paper [Reference Yang6], and is modified to describe dengue virus infecting mosquitoes. The A. aegypti female population is divided into three compartments: M 1, M 2 and M 3, which are the numbers at time t of, respectively, susceptible, exposed and infectious mosquitoes. Disregarding the transovarian transmission, all emerging mosquitoes are classified as susceptible. Similarly, the human population is divided into four compartments according to the natural history of the disease: s, e, i and r, which are the fractions at time t of, respectively, susceptible, exposed, infectious and recovered persons. The mosquito population is allowed to vary along time t, while the human population is assumed to be constant, with N being the total number of the human population.

Dengue transmission is sustained by the flows among human and mosquito compartments according to the dengue epidemic cycle presented in the previous section. Susceptible humans are infected during the bloodmeal by infectious mosquitoes, with the per capita transmission coefficient (or rate) being designated β′h, which depends on the frequency of bites given to humans by mosquitoes. The exposed persons are then transferred to the infectious class by rate α, where 1/α is the average intrinsic incubation period. These infectious individuals are removed to the recovered (immune) class after an average recovery period 1/η, where η is the recovery rate. Neither loss of immunity (we are restricted to only one serotype infection) nor induced mortality due to the disease are considered, and a constant mortality rate μ in humans is assumed. With regard to the vector, the susceptible mosquitoes are infected at a total rate βm, which is the product between the human population size N and the per capita rate β′m. It should be noted that the constant population of humans allows both coefficients βm and β′m to change according to βm=Nβ′m in every time t, making them equivalent. These exposed mosquitoes are transferred to the infectious class at a rate γ, where 1/γ is the average extrinsic incubation period, and remain infective until death. The total size of the mosquito population, which varies, is designated by M=M 1+M 2+M 3.

Based on the above considerations, the dynamics of dengue transmission can be described by

(1)
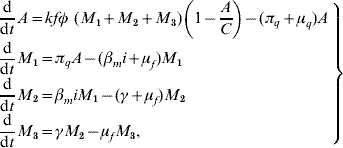
\openup1\left. {\matrix{ {\displaystyle{{\rm d} \over {{\rm d}t}}A \equals \tab kf\phi \ \lpar {M_{\setnum{1}} \plus M_{\setnum{2}} \plus M_{\setnum{3}} } \rpar \left( {1 \minus {A \over C}} \right) \minus \lpar {\pi _{q} \plus \mu _{q} } \rpar A}\hfill \cr {\displaystyle{{\rm d} \over {{\rm d}t}}M_{\setnum{1}} \equals \pi _{q} A \minus \lpar {\beta_{m} i \plus \mu _{f} } \rpar M_{\setnum{1}} } \hfill\cr {\displaystyle{{\rm d} \over {{\rm d}t}}M_{\setnum{2}} \equals \beta_{m} i M_{\setnum{1}} \minus \lpar {\gamma \plus \mu_{f} } \rpar M_{\setnum{2}} }\hfill \cr {\displaystyle{{\rm d} \over {{\rm d}t}}M_{\setnum{3}} \equals \gamma M_{\setnum{2}} \minus \mu _{f} M_{\setnum{3}} \comma }\hfill \cr} } \right\}}

in the female mosquito population, and by

(2)
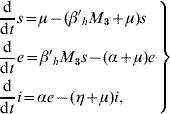
\openup3\left. {\matrix{ {\displaystyle{{\rm d} \over {{\rm d}t}}s \equals \mu \minus \lpar {\beta{^\prime}_{h} M_{\setnum{3}} \plus \mu } \rpar s} \hfill \cr {\displaystyle{{\rm d} \over {{\rm d}t}}e \equals \beta{^\prime} _{h} M_{\setnum{3}} s \minus \lpar {\alpha \plus \mu } \rpar e} \hfill \cr {\displaystyle{{\rm d} \over {{\rm d}t}}i \equals \alpha e \minus \lpar {\eta \plus \mu } \rpar i \comma } \hfill \cr} } \right\}\hfill

in the human population; where r=1−s−e−i are the (decoupled from the system) recovered individuals. The entomological parameters (see [Reference Yang6] for details) are the intrinsic oviposition rate φ, the per capita mortality rate of adult females and aquatic forms μf and μq, while πq is the per capita rate at which mosquitoes emerge from the aquatic phase. The remaining parameters are the carrying capacity C, the fraction of eggs hatching to larvae k, with 0<k<1, and the fraction of female mosquitoes hatched from all eggs f, with 0<f<1.

The system of equations (1) and (2) describes the transmission of dengue virus involving two coupled populations. This system determines the behaviour (or trajectory along time) of each compartment until reaching the steady state, which depends on the capacity of dengue transmission. The goal of the analysis of the steady state is the assessment of the control strategies to eradicate dengue transmission.

There are three equilibrium points. First, steady state is assigned by S 0 with coordinates (values of the compartments at equilibrium) Ā=1=2=3=0, =1 and ē=Ī=0. This equilibrium point is characterized by the absence of mosquitoes, and all humans are in the susceptible compartment. The second is the trivial (with regard to absence of disease) equilibrium point, which characterizes mosquito and human populations occupying the same region without propagation of dengue disease, described by S m with coordinates Ā, 1=, 2=3=0, =1 and ē=ī=0, where the coordinates of the susceptible mosquito population at equilibrium Ā and are

(3)
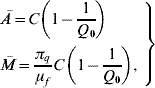
\openup1\eqalign{\left. {\matrix{{\skew 4\bar{A} \equals C\left( {1 \minus \displaystyle{1 \over {Q_{\setnum{0}} }}} \right)} \hfill \cr {\bar{M} \equals \displaystyle{{\pi _{q} } \over {\mu _{f} }}C\left( {1 \minus {1 \over {Q_{\setnum{0}} }}} \right)\comma } \hfill \cr} } \right\}\hfill

where the basic offspring number Q 0 is given by

(4)
Q_{\setnum{0}} \equals {{\pi _{q} kf\phi } \over {\lpar {\pi _{q} \plus \mu _{q} } \rpar \mu _{f} }}.\hfill

These two equilibrium points were analysed in [Reference Yang6].

Finally, the steady state corresponding to dengue settled at an endemic level S d has positive coordinates Ā, 1, 2, 3, , ē and ī given by

\openup2\left. {\matrix{{\skew 4 \hskip 6 \bar{A} \equals C\left( {1 \minus \displaystyle{1 \over {Q_{\setnum{0}} }}} \right)} \hfill \cr {\bar{M}_{\setnum{1}} \equals \displaystyle{{\lpar \gamma \plus \mu _{f} \rpar \mu _{f} \lpar \alpha \plus \mu \rpar \lpar \eta \plus \mu \rpar } \over {\beta^{\hskip1\prime}_{h} \beta_{m} \alpha \gamma \left[ {1 \minus \displaystyle{{\lpar \alpha \plus \mu \rpar \lpar \eta \plus \mu \rpar } \over {\alpha \mu }}\bar{\hskip-1\inodot}} \right]}}} \hfill \cr {\bar{M}_{\setnum{2}} \equals \displaystyle{{\mu _{f} \lpar \alpha \plus \mu \rpar \lpar \eta \plus \mu \rpar \hskip1\bar{\hskip-1\inodot}} \over {\beta^{\hskip1\prime}_{h} \alpha \gamma \left[ {1 \minus \displaystyle{{\lpar \alpha \plus \mu \rpar \lpar \eta \plus \mu \rpar } \over {\alpha \mu }}\hskip1\bar{\hskip-1\inodot}} \right]}}} \hfill \cr {\bar{M} _{\setnum{3}} \equals \displaystyle{{\lpar \alpha \plus \mu \rpar \lpar \eta \plus \mu \rpar \hskip1\bar{\hskip-1\inodot}} \over {\beta^{\hskip1\prime}_{h} \alpha \left[ {1 \minus \displaystyle{{\lpar \alpha \plus \mu \rpar \lpar \eta \plus \mu \rpar } \over {\alpha \mu }}\hskip1\bar{\hskip-1\inodot}} \right]}} } \hfill \cr} } \right\}

(with 1 being valid when ī≠0; otherwise, 1=) for the mosquito and human populations:

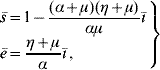
\left. {\matrix{ {\bar{s} \equals 1 \minus \displaystyle{{\lpar {\alpha \plus \mu } \rpar \lpar {\eta \plus \mu } \rpar} \over {\alpha \mu }}\hskip1\bar{\hskip-1\inodot}} \hfill \cr {\bar{e} \equals \displaystyle{{\eta \plus \mu } \over \alpha }\hskip1\bar{\hskip-1\inodot}\, \comma }\hfill \cr} } \right\}

where ī is given by

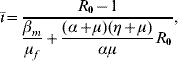
\hskip1\bar{\hskip-1\inodot} \equals \displaystyle{{R_{\setnum{0}} \minus 1} \over \displaystyle{{{\beta _{m} } \over {\mu _{f} }} \plus {{\lpar {\alpha \plus \mu } \rpar \lpar {\eta \plus \mu } \rpar} \over {\alpha \mu }}R_{\setnum{0}} }}\comma

with Q 0 being given by equation (4), and the basic reproduction number R 0 is given by

(5)
R_{\setnum{0}} \equals {{\gamma \left[ \displaystyle{{{\pi _{q} } \over {\mu _{f} }}C\left( {1 \minus {1 \over {Q_{\setnum{0}} }}} \right)} \right] \beta^{\prime}_{h} \alpha \beta _{m} } \over {\lpar {\gamma \plus \mu _{f} } \rpar \mu _{f} \lpar {\alpha \plus \mu } \rpar \lpar {\eta \plus \mu } \rpar}}\comma \hfill

where the term within square brackets in the numerator is the total number of mosquitoes in the steady state, =1+2+3. The decoupled fraction of the recovered individuals is =0 for S 0 and S m, and =1−−ē−ī, for S d.

The Appendix gives the steady-state analysis corresponding to the above three equilibrium points: the steady state regarding the mosquito-free community S 0 is stable if Q 0⩽1; the equilibrium where the community is disease-free S m, is stable if Q 0>1 and R 0⩽1; and dengue settled at an endemic level S d is stable if Q 0>1 and R 0>1. Hence, depending on the values assigned to Q 0 and R 0, one of three equilibrium points acts as an attractor. Figure 1 summarizes the basins of attraction. The changes of the attraction equilibrium point (bifurcations) in the positive parameter space (Q 0,R 0) occur for lines Q 0=1 and R 0=1. In region I (Q 0<1 and R 0<1) and in region II (Q 0<1 and R 0>1) the unique equilibrium point is S 0, which is stable. This is the reason no bifurcation occurs when line R 0=1 is crossed when passing from region I to region II. In region III (Q 0>1 and R 0<1) there exist two equilibrium points S 0 and S m, which are, respectively, unstable and stable. When passing from region I to region III, crossing line Q 0=1, one bifurcation occurs: i.e. as S m becomes stable S 0 becomes unstable. In region IV (Q 0>1 and R 0>1) there exist three equilibrium points S 0, S m and S d, which are unstable, unstable and stable, respectively. In going from region II to region IV, crossing line Q 0=1, S d becomes stable and S 0 becomes unstable; however, the passage from region III to region IV, crossing line R 0=1, results in another bifurcation: S d becomes stable and S m becomes unstable. In the accumulation point (Q 0=1 and R 0=1) any type of bifurcation can occur. Note that region II is the most dangerous, due to the fact that we can have the bifurcation from being mosquito-free to the prevalence of dengue disease in this region, if the basic offspring number can be increased, i.e. >1. This is perfectly possible if the temperature increases in this region and alters the entomological parameters in order to achieve Q 0>1.

Fig. 1. The basins of attraction considering the positive parameters Q 0 and R 0. The superscripts s and u stand for, respectively, stable and unstable.

We interpret the basic reproduction number R 0, and change βm by Nβ′m in equation (5). In terms of the per capita dengue transmission coefficients β′h and β′m, R 0 can be rewritten as

(6)
R_{\setnum{0}} \equals {\gamma \over {\gamma \plus \mu_{f} }} \times {{\bar{M} \beta^{\hskip0.5\prime}_{\hskip-0.5 h} } \over {\mu _{f} }} \times {\alpha \over {\alpha \plus \mu }} \times {{N\beta^{\hskip1\prime}}_{\hskip-4 m} \over {\eta \plus \mu }}.\hfill

Assume that one infectious mosquito is introduced into a completely susceptible population of mosquitoes and humans, which have potentially infective sizes and N, respectively. This uniquely infectious mosquito bites an average β′h/μf number of susceptible humans (β′h/μf is the per capita number of bites) during the infectious period. Afterwards, these exposed humans must survive the intrinsic incubation period, with probability α/(α+μ), and, then, are bitten on average by Nβ′w/(η+μ), the number of susceptible mosquitoes during the infectious period. Finally, the probability that these exposed mosquitoes survive the extrinsic incubation period and become infectious mosquitoes is given by γ/(γ+μf). Therefore, R 0 is the average number of secondary infectious mosquitoes produced by one infectious mosquito introduced into a completely homogeneous and susceptible population of mosquitoes and humans. For this reason, dengue epidemics fade out if the average number of secondary infections is lower than unity. This number also measures both the severity of the infection in a community and the efforts necessary to eradicate the epidemic. The introduction of one infectious human follows a similar pattern.

There are two ways to define the per capita incidence [Reference Li12]. One is to assume that the rate of new infections occurs according to the contact between the numbers of susceptible and infectious individuals. In this case we use the per capita transmission coefficients β′h and β′m, and this kind of modelling is known as the ‘pseudo’ mass action law. On the other hand, the ‘true’ mass action law considers the fractions of susceptible and infectious individuals, using the total transmission coefficients βh and βm. When the populations are not allowed to vary (constant) in time, both kind of mass action laws are interchangeable. However, the figure is completely different when one or more populations are allowed to vary. In our case, the mosquito population is allowed to vary, while the human population is maintained constant. Hence, the infection in mosquitoes does not matter in the formulae for the basic reproduction number.

In equation (6) the expression for R 0 arises due to the assumption of the ‘pseudo’ mass action law for infection in humans (the per capita incidence is proportional to the number of infectious mosquitoes, β′hM 3), and it can be written as

R_{\setnum{0}} \equals {{\beta^{\hskip1\prime}_{h} \beta^{\hskip1\prime}_{\hskip-1 m} } \over {\beta ^{th} }}\comma

where βth is the threshold transmission coefficient involving the product of the per capita dengue transmission coefficients β′h and β′m, given by

(7)
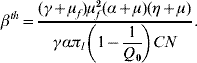
\beta ^{th} \equals {{\lpar {\gamma \plus \mu _{f} } \rpar \mu _{f}^{\setnum{2}} \lpar {\alpha \plus \mu } \rpar \lpar {\eta \plus \mu } \rpar} \over {\gamma \alpha \pi _{l} \left( {1 \minus \displaystyle{1 \over {Q_{\setnum{0}} }}} \right)CN}}.\hfill

When Q 0<1, we have a human population living free of mosquitoes, and this situation is strongly robust. Note that the absence of mosquito population resulted in βth<0, which mathematically means R 0<0, but biologically is meaningless. Hence, the dengue risk is real and can be measured if Q 0 increases and becomes >1, in which case R 0 becomes positive. As Q 0 increases, βth decreases, and eventually surpasses the threshold value β′hβ′m, yielding R 0>1 at which point dengue epidemics can be triggered.

However, the ‘true’ mass action law yields the basic reproduction number expressed in terms of the total transmission coefficients, because we must use the total transmission coefficient βh in equation (2), i.e. we must substitute β′hM 3 by βhM 3/M, since

\beta^{\hskip1\prime}_{h} M_{\setnum{3}} \equals M\beta^{\hskip1\prime}_{\hskip-1h} {{M_{\setnum{3}} } \over M} \equals \beta _{h} {{M_{\setnum{3}} } \over {M_{\setnum{1}} \plus M_{\setnum{2}} \plus M_{\setnum{3}} }}.

Due to the appearance of the fraction of infectious mosquitoes, we implicitly assume that M>0, or, equivalently, Q 0>1. Hence, by changing β′h to βh and Nβ′m to βm in equation (6), the basic reproduction number R 0 can be written as

R_{\setnum{0}} \equals {{\beta _{h} \beta _{m} } \over {\bar{\beta }^{th} }}\comma

where \bar{\beta }^{th} is the threshold transmission coefficient involving the product of the total dengue transmission coefficients βh and βm, given by

(8)
\bar{\beta }^{th} \equals {{\lpar {\gamma \plus \mu _{f} } \rpar\mu _{f} \lpar {\alpha \plus \mu } \rpar \lpar {\eta \plus \mu } \rpar} \over {\gamma \alpha }}.\hfill

Note that \bar{\beta }^{th}does not depend on the mosquito and human populations and N as does \bar{\beta }^{th}. Therefore \bar{\beta }^{th} never assumes a negative value.

When there is an absence of good estimates for the dengue transmission coefficients β′h and β′m (or βh and βm), then βth or \bar{\beta }^{th} can be used instead to assess the potential risk of dengue epidemics. Note that the chance of a dengue outbreak increases inversely proportional to the threshold transmission coefficients. The threshold transmission coefficient βth and the basic offspring number Q 0, which appear in its definition, depend on all entomological parameters, while the threshold transmission coefficient \bar{\beta }^{th} depends only on the mortality rate of female mosquitoes μf.

In next section we assess the effects of temperature on dengue transmission.

ASSESSING THE EFFECTS OF TEMPERATURE ON DENGUE RISK

The ecological and epidemiological results obtained from the mathematical modelling reported in [Reference Yang6] are used to assess the risk of dengue depending on temperature.

As stated in the previous section, the intrinsic and extrinsic incubation periods, 1/α and 1/γ, are assumed to be constant with temperature. Therefore, the risk of a dengue outbreak is assessed by taking into account only the variations in the entomological parameters with temperature. Figure 2 gives the threshold transmission coefficients βth and \bar{\beta }^{th} as a function of temperature. The curve corresponding to the threshold transmission coefficient βth was obtained using NC=1; however, by increasing this value tenfold, the curve moves down one unity (using log-scale), decreasing the threshold transmission coefficient \bar{\beta }^{th}, and, consequently, increasing the possibility of a dengue outbreak. In the case of \bar{\beta }^{th}, which depends on the temperature only through the mortality rate of female mosquitoes and does not depend on N and C explicitly, we observe a very low sensitivity for temperature. Because in this model (‘true’ mass action law) it is implicitly assumed that the mosquito population exists, we must take into account the regions where mosquitoes are prevalent, Q 0>1, as well as β′h β′m>\bar{\beta }^{th}.

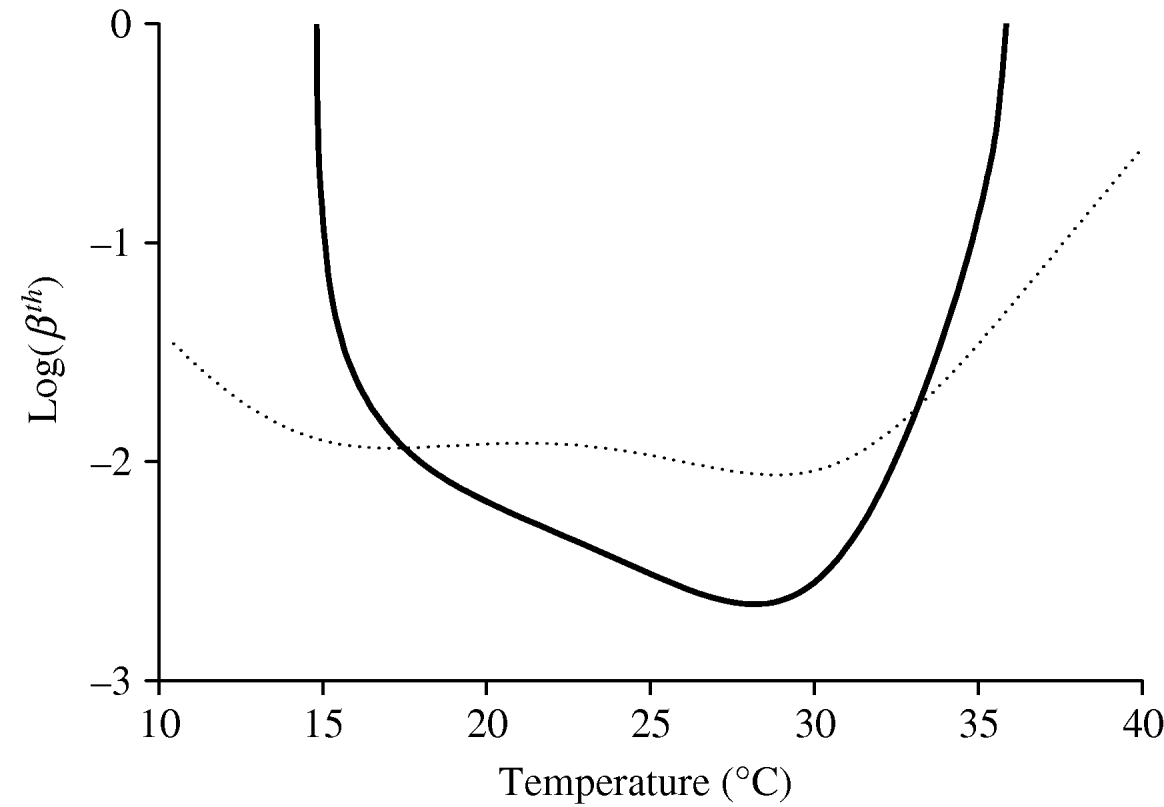
Fig. 2. The threshold transmission coefficients βth and \bar{\beta }^{th} as a function of temperature are shown. The thick curve corresponds to βth, while the dotted curve corresponds to \bar{\beta }^{th}. The risk of dengue epidemics is high (and the epidemics settle at a high level) for lower values of the threshold transmission coefficients. We set α=0·2, γ=0·125, η=0·25 and μ=0·000043 (all in days−1).

When there are no precise estimates of the transmission coefficients, the corresponding threshold values can be seen as an alternative for assessing dengue outbreaks or the severity of dengue epidemics. With regard to the curve corresponding to βth in Figure 2, if we assume that the transmission coefficients in a certain geographic region are βhS and βmS, a horizontal line can be drawn with value log (βhS βmS) in the log(βth)×T coordinates, which intercepts the curve βth at two temperatures, i.e. T 1 and T 2. If this selected region is situated between T 1 and T 2, dengue epidemics can be triggered, and the temperature at which the level of the epidemic is most severe is ~28°C, where βth assumes the lowest value. This finding shows that the increase in temperature, e.g. due to global warming, does not necessarily increase the incidence of dengue disease.

The basic reproduction ratio R 0 is a quotient between the product of transmission coefficients and the corresponding threshold value. For this reason, the difference between them, defined by βth−βh βm, to some extent measures the welfare of a community (or region) regarding dengue disease. If this difference is positive and very high, the community is practically free of dengue outbreaks (i.e. βh βm<βth); otherwise, if this difference is negative and very high, dengue outbreaks will be very severe. However, the levels of recurrent dengue epidemics are not only dependent on the transmission coefficients, but also on the fractions of the susceptible populations of mosquitoes and humans: if both fractions are almost 1 (exactly 1 when dengue disease is introduced into completely susceptible populations), the next dengue outbreak will be more severe [Reference Yang13].

The basic reproduction ratio R 0 depends on the transmission coefficients, which are assumed to be temperature independent. However, both parameters are dependent on the number of bites that a female mosquito gives to humans in order to mature the fertilized eggs. Our companion paper [Reference Yang6], shows that the oviposition is absent at low temperature, and this number increases with temperature, practically in line with temperature from 15°C, and decreases for high temperature. If the number of bites is approximated with the number of eggs laid by female mosquitoes, the capacity of the vector to transmit the disease is limited to the extreme temperatures. Note that at around 15–16°C, the first day at which female mosquitoes laid eggs, is higher than for 15 days, and discounting the time necessary to mature fertilized eggs, we have day 12 as the age of the mosquitoes first biting. This indicates that the biting behaviour of female mosquitoes is delayed, and when compared with the extrinsic incubation period of around 10 days, the possibility of dengue virus inoculation in humans is not negligible, because female mosquitoes survive for around 30 days [Reference Yang6]. Even allowing the transmission coefficients to vary with temperature, Figure 2 is a good indicator of the risk of dengue according to temperature.

The basins of attraction in Figure 1 shed some lights on the invasion and colonization by A. aegypti and the outbreak of dengue epidemics. Let us apply these findings to São Paulo State, Brazil. São Paulo State can be approximated roughly by a parallelogram of dimension 690 km in the northwest-southwest direction and 440 km in the northeast-southwest direction. The Atlantic Ocean is at the southern frontier, and Mato Grosso State at the northern border. At the eastern side, there are two states: Rio de Janeiro occupying a small part in the extreme of the southern frontier, and Minas Gerais State occupying almost the entire eastern frontier. At the western frontier is Paraná State.

São Paulo State is situated in a subtropical region, with a hot and rainy summer season, where the mosquito A. aegypti was re-introduced in 1985 from the northern border, and advanced continuously in a southerly direction [Reference Glasser14]. The A. aegypti invasion initiated from Mato Grosso State and followed a southerly direction, to the Atlantic Ocean, where the mosquitoes arrived in 1994 [Reference Maidana and Yang15]. The northern region of São Paulo State is characterized by an annual mean temperature of >18°C and an annual mean rainfall of <1400 mm, while the middle region of São Paulo State has an annual mean temperature and rainfall of, respectively, 17°C and 1500 mm [Reference Glasser14].

After colonization by A. aegypti, dengue epidemics were first observed in 1987, but systematical and annual occurrences of epidemics started in 1990. According to the Epidemiological Vigilance Centre [16, 17], the number of cases of dengue from 1995 until 2007 were, respectively, 6048, 7104, 2040, 10 630, 15 082, 3532, 51 668, 39 179, 20 390, 3049, 5433, 50 022 and 90 252.

However, there is a belt of tropical forest (Mata Atlântica), 80 km from the Atlantic Ocean, where the annual mean temperature is low. In this region São Paulo City and its neighbouring cities are situated, comprising ~20 million inhabitants. Due to low temperature in winter seasons, this region is relatively safe from dengue colonization, in spite of the recent sporadic dengue epidemics that occurred in the outskirts of São Paulo City during the summer seasons.

Excluding a small tropical forest belt, São Paulo State can be matched with region IV in the basins of attraction shown in Figure 1. This region is characterized by Q 0>1 and R 0>1, for this reason A. aegypti was successfully introduced in 1985 (bifurcation from S 0 to S m, both equilibria unstable), and in 1990, dengue disease settled at an endemic level (bifurcation from S m to S d, the latter equilibrium stable). However, the region comprising São Paulo City and its surrounding cities can be matched with region II (Fig. 1), because the invasion and colonization by mosquitoes had already occurred in all frontiers of this region. Additionally, this region is heavily populated and there is an abundance of a variety of breeding sites capable of receiving eggs and developing immature forms. As this region is characterized by Q 0<1 and R 0>1, an increase in temperature may increase the basic offspring number to >1 and drive to region IV. A bifurcation from absence of mosquitoes to the onset of dengue epidemics can then be observed (bifurcation from S 0 to S m and then, S m to S d; or a dangerous bifurcation from S 0 to S d).

DISCUSSION AND CONCLUSION

We developed a mathematical model to in order to assess the effects of temperature on the risk of dengue outbreak.

To assess the effects of temperature on dengue epidemics, we yielded the basic reproduction number R 0. In the absence of real estimates for dengue transmission coefficients, we took, as the risk factor of dengue epidemics, the threshold transmission coefficient βth or \bar{\beta }^{th}, in the sense that the lower this threshold number, the higher was the possibility of dengue outbreak. In particular, the curve for βth (Fig. 2) is roughly inverse with respect to the curve obtained for Q 0 (see [Reference Yang6]), and one reason for this behaviour is that we did not allow the disease-related parameters (intrinsic and extrinsic incubation periods and recovery rate) to vary with temperature. Hence, the basic offspring number Q 0 can be taken as the measure of the potential risk of dengue outbreak and also with regard to the severity of dengue epidemics. It should be noted that the temperature at which the lowest value for βth occurs is 28·0°C, which is 1·2°C lower than the temperature at which the maximum value for Q 0 occurs (see [Reference Yang6]).

In our companion paper [Reference Yang6] we conjectured that female mosquitoes survive for the same periods of time during the interval 15<T<30°C, because they bite more and require greater physiological efforts to maturate fertilized eggs. Moreover, dengue virus could potentially increase the lifespan of infected mosquitoes without decreasing their biting activities. The basic reproduction number R 0 depends linearly on the lifespan of female mosquitoes, 1/μf, according to equation (5). Then, the spread of dengue disease increases due to the virus activities inside the infected mosquitoes and also due to the fact that the biting activities increase with temperature.

Finally, in the present study we dealt with annual mean entomological values. In a further paper, we will allow the entomological parameters to vary with time, and, consequently, to vary with temperature, and will perform the sensitivity analysis of the basic offspring number and basic reproduction number for the entomological parameters. The varying size of the mosquito population will be matched to the seasonally varying number of dengue cases in order to estimate the transmission coefficients.

APPENDIX A

Steady states

We present the stability analysis of the equilibrium points S 0, S m and S d. The local stability analysis (some basic ideas about stability analysis is given in [Reference Yang6]) is assessed to determine the roots of the characteristic equation Λ(λ)≡det (J*−λI), where J* is the Jacobian matrix corresponding to the system of equations (1) and (2) evaluated at one of the equilibrium points S 0, S m and S d, and I is a 7×7 identity matrix.

The roots of the characteristic equation corresponding to the mosquito-free community S 0 are

\hskip -23pt\eqalign{ \lambda _{\setnum{1}} \equals \tab \minus \lpar \eta \plus \mu \rpar \comma \lambda _{\setnum{2}} \equals \minus \lpar \alpha \plus \mu \rpar \comma \lambda _{\setnum{3}} \equals \minus \mu \comma \lambda _{\setnum{4}} \equals \minus \mu_{f} \comma \cr \lambda _{\setnum{5}} \equals \tab \minus \lpar \gamma \plus \mu_{f} \rpar \comma \cr}

and the remaining two solutions are those given in [Reference Yang6]. Hence, equilibrium point S 0 is locally asymptotically stable if Q 0<1.

To show the global stability of the equilibrium point S 0, note that the region of biological interest Ω, defined as

\rmOmega \equals \lcub \lpar A\comma M_{\setnum{1}} \comma M_{\setnum{2}} \comma M_{\setnum{3}} \comma s\comma e\comma i\rpar \in {\rm R}_{ \plus }^{\setnum{7}} \vert 0\les A\les C\comma s \plus e \plus i\les 1\rcub \hfill

is positively invariant for the system of equations (1) and (2). The global stability of the equilibrium point S 0 can be proved for Q 0⩽1 using the function V:R +7→R given by

V \equals {{\pi _{q} } \over {\pi _{q} \plus \mu _{q} }}A \plus M_{\setnum{1}} \plus M_{\setnum{2}} \plus M_{\setnum{3}} \comma \hfill

whose orbital derivative is

\dot{V} \equals \minus \mu _{f} \left[ {{{Q_{\setnum{0}} A} \over C} \plus \lpar {1 \minus Q_{\setnum{0}} } \rpar} \right]\lpar {M_{\setnum{1}} \plus M_{\setnum{2}} \plus M_{\setnum{3}} } \rpar.\hfill

Note that <0 for Q 0<1, and for Q 0=1 we have =0 if M 1+M 2+M 3=M=0 or A=0. From inspection of equation (1) it can be seen that the maximal invariant set contained in =0 is the trivial equilibrium point S 0. Then, from La Salle–Lyapunov Theorem [Reference Hale18], the equilibrium point S 0 is globally asymptotically stable for Q 0⩽1. Hence, the human population living without mosquitoes is a robust situation, and humans are protected against dengue epidemics.

One of the roots of the characteristic equation corresponding to the disease-free community S m is λ1=−μ. Two other roots are solutions given in [Reference Yang6], which have negative real part if Q 0>1. The remaining four roots are solutions of the equation

\rmLambda _{c} \lpar \lambda \rpar \equals \lambda ^{\setnum{4}} \plus c_{\setnum{3}} \lambda ^{\setnum{3}} \plus c_{\setnum{2}} \lambda ^{\setnum{2}} \plus c_{\setnum{1}} \lambda \plus c_{\setnum{0}} \comma \hfill

where the coefficients are

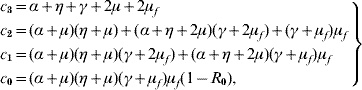
\hskip-3\eqalign{\left. {\matrix{ {c_{\setnum{3}} \equals \alpha \plus \eta \plus \gamma \plus 2\mu \plus 2\mu _{f} } \hfill \cr {c_{\setnum{2}} \equals \lpar {\alpha \plus \mu } \rpar \lpar {\eta \plus \mu } \rpar \plus \lpar {\alpha \plus \eta \plus 2\mu } \rpar \lpar {\gamma \plus 2\mu _{f} } \rpar \plus \lpar {\gamma \plus \mu _{f} } \rpar\mu _{f} }\hfill \cr {c_{\setnum{1}} \equals \lpar {\alpha \plus \mu } \rpar \lpar {\eta \plus \mu } \rpar \lpar {\gamma \plus 2\mu _{f} } \rpar \plus \lpar {\alpha \plus \eta \plus 2\mu } \rpar \lpar {\gamma \plus \mu _{f} } \rpar \mu _{f} } \hfill \cr {c_{\setnum{0}} \equals \lpar {\alpha \plus \mu } \rpar\lpar {\eta \plus \mu } \rpar \lpar {\gamma \plus \mu _{f} } \rpar\mu _{f} \lpar {1 \minus R_{\setnum{0}} } \rpar \comma } \hfill\cr} } \big\right\}\hfill

with the basic reproduction number R 0 being given by equation (5). When R 0<1, the polynomial Λc (λ) as all solutions with negative part real, because the Routh–Hurwitz criteria [Reference Edelstein-Keshet19] c 3>0, c 1>0, c 0>0 and c 3c 2c 1>c 12+c 32c 0 are satisfied. The last inequality can be rewritten as

{{c_{\setnum{1}} \lpar c_{\setnum{3}} c_{\setnum{2}}\minus c_{\setnum{1}} \rpar \minus c_{\setnum{3}}^{\setnum{2}} \lpar \alpha \plus \mu \rpar \lpar \eta \plus \mu \rpar \lpar \gamma \plus \mu _{f} \rpar \mu _{f} } \over {c_{\setnum{3}}^{\setnum{2}} }} \hskip -1\gt \hskip -2\minus \alpha \gamma \bar{M}\beta^{\hskip1\prime}_{\hskip -1h} \beta_{m} \comma

and we have shown that c 1 (c 3c 2−c 1)−c 32 (α+μ) (η+μ) (γ+μf)μf>0. Hence, equilibrium point S m is locally asymptotically stable if Q 0>1 and R 0<1.

The characteristic equation corresponding to dengue disease settled at an endemic level S d is given by Λ(λ)=−Λb(λ)Λ5(λ), where Λb(λ) is that given in [Reference Yang6] (Q 0>1 to satisfy Routh–Hurwitz criteria), and

\hskip-2\eqalign{ \rmLambda _{\setnum{5}} \lpar \lambda \rpar \equals \tab \lpar \beta _{m} \bar{\inodot} \plus \mu _{f} \plus \lambda \rpar \lpar \bar{M}_{\setnum{3}} \beta^{\hskip1\prime}_{h} \plus \mu \plus \lambda \rpar \lpar \alpha \plus \mu \plus \lambda \rpar \hfill \cr \tab \times \lpar \eta \plus \mu \plus \lambda \rpar \lpar \gamma \plus \mu _{f} \plus \lambda \rpar \minus \alpha \gamma \bar{M}_{\setnum{1}} \beta^{\hskip1\prime}_{h} \beta _{m} \bar{s}\ \lpar \mu \plus \lambda \rpar \comma \hfill \cr}

where the independent term is given by

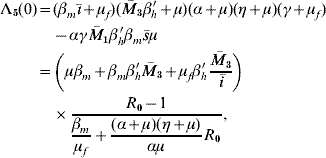
\hskip-24\eqalign{ \rmLambda _{\setnum{5}} \lpar 0\rpar \equals \tab \lpar \beta _{m} \bar{\inodot} \plus \mu _{f} \rpar \lpar \bar{M} _{\setnum{3}} \beta^{\hskip1\prime}_{h} \plus \mu \rpar \lpar \alpha \plus \mu \rpar \lpar \eta \plus \mu \rpar \lpar \gamma \plus \mu _{f} \rpar \hfill \cr \tab \minus \alpha \gamma \bar{M} _{\setnum{1}}\beta^{\hskip1\prime}_{h} \beta_{m} \bar{s}\mu \cr \equals \tab\left( {\mu \beta _{m} \plus \beta _{m} \beta^{\hskip1\prime}_{h} \bar{M} _{\setnum{3}} \plus \mu _{f} \beta^{\hskip1\prime}_{h} {{\bar{M} _{\setnum{3}} } \over {\bar{i}}}} \right) \cr \tab \times \displaystyle{{R_{\setnum{0}} \minus 1} \over \displaystyle{{{\beta _{m} } \over {\mu _{f} }} \plus {{\lpar \alpha \plus \mu \rpar \lpar \eta \plus \mu \rpar } \over {\alpha \mu }}R_{\setnum{0}} }}\comma \cr}

with ī>0 and 3>0. This term is positive if R 0>1, and according to conjecture in [20], Λ5(λ) has all solutions with negative part real. Remembering that Λb(λ) has solutions with negative real part if Q 0>1, then the non-trivial equilibrium point S d is locally asymptotically stable when R 0>1 and Q 0>1.

ACKNOWLEDGEMENTS

This work was supported by grant from FAPESP (Polìticas Públicas and Temático). H.M.Y. thanks the CNPq for the award of a fellowship. Thanks are also due to anonymous referees for comments and suggestions, which contributed to the improvement of this paper.

DECLARATION OF INTEREST

None.

References

REFERENCES

1. Mandell, GL, Bennett, JE, Dolin, R. Mandell, Douglas, and Bennett's Principles and Practice of Infectious Diseases. Philadelphia: Elsevier Inc., 2005, pp. 3662.Google Scholar
2. Tripet, F, Aboagye-Antwi, F, Hurd, H. Ecological immunology of mosquito-malaria interactions. Trends in Parasitology 2008; 24: 219–227.CrossRefGoogle ScholarPubMed
3. Veronesi, R. Doenças Infecciosas e Parasitárias. Rio de Janeiro: Ed. Guanabara Koogan, 1991, pp. 1082.Google Scholar
4. Nelson, MJ. Aedes aegypti: Biologia y Ecologia, Washington, DC: Organización Panamericana de la Salud, 1986, pp. 50.Google Scholar
5. Rueda, LM, et al. Temperature development and survival rates of Culex quinquefasciatus and Aedes aegypti (Diptera: Culicidae). Journal of Medical Entomology 1990; 27: 892–898.CrossRefGoogle ScholarPubMed
6. Yang, HM, et al. Assessing the effects of temperature on the population of Aedes aegypti, the vector of dengue. Epidemiology and Infection 2009. doi:10.1017/S0950268809002040.Google ScholarPubMed
7. Esteva, L, Vargas, C. Coexistence of different serotypes of dengue virus. Journal of Mathematical Biology 2003; 46: 31–47.CrossRefGoogle ScholarPubMed
8. Esteva, L, Yang, HM. Mathematical model to assess the control of Aedes aegypti mosquitoes by the sterile insect technique. Mathematical Biosciences 2005; 198: 132–147.CrossRefGoogle ScholarPubMed
9. Feng, Z, Velasco-Hernandez, V. Competitive exclusion in a vector-host model for the dengue fever. Journal of Mathematical Biology 1996; 35: 523–544.CrossRefGoogle Scholar
10. Newton, EA, Reiter, A. A model of the transmission of dengue fever with an evaluation of the impact of ultra-low-volume (ULV) insecticide applications on dengue epidemics. American Journal of Tropical Medicine and Hygiene 1992; 47: 709–720.CrossRefGoogle Scholar
11. Lindsay, SW, Birley, MH. Review: climate change and malaria transmission. Annals of Tropical Medicine and Parasitology 1996; 90: 573–588.CrossRefGoogle ScholarPubMed
12. Li, MY et al. Global dynamics of a SEIR model with varying total population size. Mathematical Biosciences 1999; 160: 191–213.CrossRefGoogle ScholarPubMed
13. Yang, HM. Modelling vaccination strategy against directly transmitted diseases using a series of pulses. Journal of Biological Systems 1998; 6: 187–212.CrossRefGoogle Scholar
14. Glasser, CM. Study of the infestation of the State of São Paulo by Aedes aegypti and Aedes albopictus [in Portuguese]. Dissertation, FSP, Universidade de São Paulo, São Paulo, 1997.Google Scholar
15. Maidana, NA, Yang, HM. Describing the geographic propagation of dengue disease by travelling waves. Mathematical Biosciences 2008; 215: 64–77.CrossRefGoogle Scholar
16. Epidemiological Vigilance Centre (http://www.cve.saude.sp.gov.br/htm/zoo/den_dir06.htm). Accessed 27 September 2007.Google Scholar
17. Epidemiological Vigilance Centre (http://www.cve.saude.sp.gov.br/htm/zoo/den_2se07.htm). Accessed 10 April 2008.Google Scholar
18. Hale, JK. Ordinary Differential Equations. New York: John Wiley and Sons, 1969, pp. 332.Google Scholar
19. Edelstein-Keshet, L. Mathematical Models in Biology (Birkhäuser Mathematics Series). New York: McGraw-Hill Inc., 1988, pp. 586.Google Scholar
20. Leite, MBF, Bassanezi, RC, Yang, HM. The basic reproduction ratio for a model of directly transmitted infections considering the virus charge and the immunological response. IMA Journal of Mathematics Applied in Medicine and Biology 2000; 17: 15–31.CrossRefGoogle Scholar
Figure 0

Fig. 1. The basins of attraction considering the positive parameters Q0 and R0. The superscripts s and u stand for, respectively, stable and unstable.

Figure 1

Fig. 2. The threshold transmission coefficients βth and \bar{\beta }^{th} as a function of temperature are shown. The thick curve corresponds to βth, while the dotted curve corresponds to \bar{\beta }^{th}. The risk of dengue epidemics is high (and the epidemics settle at a high level) for lower values of the threshold transmission coefficients. We set α=0·2, γ=0·125, η=0·25 and μ=0·000043 (all in days−1).