INTRODUCTION
Pertussis remains a cause of public health concern in the United States despite the dramatic success of childhood pertussis vaccination [Reference Cherry1]. Pertussis is still endemic among infants, the age group most at risk of morbidity, hospitalization and mortality [Reference Cherry1]. Furthermore, since the 1980s, rates of pertussis in North America have been rising among adolescents and adults [2], the population groups who are increasingly recognized as vectors for Bordetella pertussis transmission to infants [Reference Broder3–6]. The true burden of pertussis is unknown partly due to the atypical presentation of infection in adolescents and adults as well as the under-reporting of pertussis [Reference Broder3].
Acellular pertussis vaccines combined with tetanus and diphteria (Tdap) vaccines that provide high levels of immunogenicity in adults and adolescents have recently become available [Reference Halperin4, Reference Ward5], and were approved by the US Food and Drug Administration in 2005. In 2006, the American Committee on Immunization Practices (ACIP) issued final recommendations for their use on adolescents [Reference Broder3] and adults [6]. Recommendations for adults include the ‘cocoon’ vaccination (vaccination of close contacts of newborns) and replacement of the next Td (tetanus–diphteria) booster by a Tdap vaccine.
The impact of pertussis vaccination strategies involving adolescents and/or adults in the United States has been assessed using computer models [Reference Hethcote7, Reference Van Rie and Hethcote8]. Since the publication of these studies [Reference Van Rie and Hethcote8], a host of key data have become available for the United States, including a more accurate estimation of pertussis incidence among adolescents and adults [Reference Ward5], vaccine effectiveness by dose of vaccine administered [Reference Bisgard9], the sources of pertussis transmission to young infants, and the contribution of asymptomatic infection to the transmission of B. pertussis [Reference Wendelboe10].
The main objective of the present study was to use these new key data in order to improve the prediction of the impact of the implementation of the newly recommended adult vaccination strategies on pertussis infection rates in the United States (Table 1).
Table 1. Vaccination strategies considered

METHODS
A compartmental age-structured pertussis model
The starting point for the present study was the model developed by Van Rie & Hethcote, which has been described in detail [Reference Hethcote7, Reference Van Rie and Hethcote8]. Briefly, the population is compartmentalized based on immunity to pertussis infection and infection status: susceptible (full or partial), immune and infected. The transition of an individual's immune status and associated risk of infection is shown by the direction of the arrows in Figure 1. Infections can be typical (paroxysmal cough of at least 3 weeks' duration) [11], mild (cough of less than 3 weeks' duration) or asymptomatic. The mean time during which an individual with pertussis was considered infectious was 4 weeks for a typical case, 3 weeks for a mild case, and 1 week for an asymptomatic case.

Fig. 1. Diagram of the immunological and infectious states and transitions between states in the age-specific pertussis model. WN1–3, Waning of natural immunity 1–3; V1–V4, vaccination status 1–4; WV1–3, waning vaccine 1–3; vc, vaccine coverage.
An individual's risk of progression to disease upon exposure is determined by the level of immunity, which depends on
• vaccination status, depending on the number of doses received (compartments V1–V4);
• the eventual waning of vaccine-induced immunity that may occur whatever the number of doses received (compartments WV1–WV3);
• natural immunity post-infection and the waning of natural immunity (compartments WN1–WN3).
The waning of natural or vaccine-induced immunity can be halted and immunity restored by vaccination (vc). The median residence time in each of the naturally acquired immunity compartments was taken as 8 years, and the median residence time in each of the vaccine-induced immunity compartments was 4 years, ranging from 2 to 8 years in sensitivity analyses. A mathematical description of the model is given in Appendix 1.
Data on child spacing and multiple births were used to adjust the number of parents to be vaccinated in the cocoon strategy. When this strategy is implemented, women who deliver more than 5 years after the last vaccination receive a booster dose. Following Van Rie & Hetchcote [Reference Van Rie and Hethcote8], the fraction of women vaccinated for the ‘cocoon’ strategy is given by the coverage rate associated to this strategy multiplied by 0·88 in the first year, 0·87 in the second year, 0·77 in the third year, 0·65 in the fourth year, and subsequently 0·57 annually. The ratio of vaccinated women to vaccinated male partners was 1:0·74.
Update of key parameters and model structure
Compared with previous analyses [Reference Hethcote7, Reference Van Rie and Hethcote8], the model was modified in five key areas in order to: (1) update the probability of developing pertussis after exposure to B. pertussis using recently published data of efficacy per dose administered; (2) determine age-specific forces of infection based on recent US incidence data instead of pre-vaccine era seroprevalence data; (3) revise the role of asymptomatic infection in the transmission of B. pertussis; (4) use recent data on sources of transmission of B. pertussis to young infants, and (5) factor in US population growth over time.
The first three sets of parameters were updated using a specific calibration procedure based on an expectation-minimization algorithm (See Appendix 2 for technical details).
Vaccine efficacy
Vaccine efficacy data used in the model were based on a recent case-controlled study of infant pertussis vaccination [Reference Bisgard9], and the randomized controlled Adult Pertussis (APERT) trial of a booster dose for adolescents and adults [Reference Van Rie and Hethcote8]. For infants, the results reported for the 6–23 months age group were used as they are the most conservative and because the result in the 24–59 months age group is based on a small proportion of vaccinated children (⩽2%) likely to have an atypical profile. The estimates for vaccine efficacy used were thus 46·0% [95% confidence intervals (CI) 0·0–88·2] after the first dose, 79·6% (95% CI 24·6–94·5) after the second, 91·7% (95% CI 74·5–97·3) after the third and 96·4% (95% CI 86·4–99·0) after the fourth dose [Reference Bisgard9]. Based on the APERT trial results, we used a 92% (95% CI 32–99) vaccine efficacy for the booster dose administered to adults with a median age of 35 years [Reference Van Rie and Hethcote8].
These estimates do not allow direct assessment of the specific protection conferred by vaccination against typical, mild and asymptomatic pertussis infection. We therefore assumed the existence of a latent variable with normal distribution for the severity of pertussis infection. For symptomatic infections, this severity variable was characterized by the duration of cough (a severity >3 represented typical infection). The mean and standard deviation of its distribution were determined using the distribution of severity of cases among fully susceptible individuals (73% severe pertussis, 25% mild and 2% asymptomatic). The impact of vaccination, and the overall reduction of pertussis severity following exposure, was expressed by a reduction of the mean of this distribution in each vaccine-related compartment (V1–V4, WV1–WV3). The calibration procedure was used to identify the reduction that fits best with data reported by Bisgard et al. [Reference Bisgard9] and Ward et al. [Reference Ward5]. The resulting estimated probabilities of individuals developing a typical, mild or asymptomatic infection in the different compartments are presented in Table 2. Compared to the parameters used by Van Rie & Hethcote [Reference Hethcote7, Reference Van Rie and Hethcote8], the estimates result in a higher efficacy of infant vaccination and a greater impact of the waning of vaccine efficacy.
Table 2. Distribution of outcomes in case of contact with an infectious person according to immunological status

* Value for vaccine-related compartments estimated using Bisgard et al. [Reference Bisgard9] and Ward et al. [Reference Ward5]. Figures in parentheses define the variation interval used in sensitivity analyses and results from the calibration procedure performed.
Pertussis incidence and force of infection
The data from the recent APERT trial in the United States [Reference Ward5] in combination with age-specific data for US adolescents and adults from 2004 [Reference Purdy12] were used to characterize the incidence of symptomatic pertussis cases in subjects aged ⩾10 years. The incidence of adult pertussis in the childhood vaccine era, as determined by the APERT trial was 370/100 000 person-years (95% CI 176–576). For the incidence of symptomatic pertussis cases among children aged <10 years, we used the most recent CDC surveillance data from 2004 [Reference Jajosky13] in combination with age-specific reporting rates [Reference Sutter and Cochi14] to account for the known under-reporting of surveillance data. The result of these estimates (Fig. 2b) lead to a similar distribution of age-specific forces of infection to that published by Van Rie & Hethcote [Reference Van Rie and Hethcote8], but with different absolute values.

Fig. 2. (a) Annual, age-specific incidence of pertussis (■, typical cases; □, mild cases) derived from the model for the current vaccination schedule (base case). (b) Comparison of the age-specific force of infection in absence of vaccination used in Van Rie & Hethcote [Reference Van Rie and Hethcote8] and derived from US data in this analysis.
In a second step, estimated age-specific forces of infection were used to identify age-specific transmission parameters that form the WAIFW (who acquires infection from whom) matrices considered in this analysis. The structure of the WAIFW matrix considered in the base case is directly derived from the one used in Van Rie & Hethcote [Reference Van Rie and Hethcote8]. Since the structure of the WAIFW matrix plays an important role in disease dynamics, we tested two other matrices in the sensitivity analysis. These two matrices correspond to extreme situations: (1) contacts occurring among individuals belonging to the same age group (assortative mixing), and (2) identical level of contact whatever the age of the infective (age-dependent transmission rates).
The role of asymptomatic pertussis cases in disease transmission
The contribution of transmission from individuals with asymptomatic or subclinical pertussis infection is not well defined. Results of a recent study suggest that asymptomatic or subclinical infection may contribute to about 16% of cases of disease transmission for infants aged <6 months [Reference Wendelboe10]. We adjusted the relative infectivity of a case of asymptomatic infection to fit a 16% contribution of asymptomatic infections to B. pertussis transmission in the base case scenario, and obtained a relative infectivity of asymptomatic infections of 0·915 (the reference value is 1 for both typical and mild cases). The extent of disease transmission attributable to asymptomatic pertussis infections in the model is based on three factors: the number of asymptomatic pertussis infections, the average infectious period for an asymptomatic case (1 week, compared with 4 weeks for typical pertussis cases and 3 weeks for mild cases), and the adjusted relative infectivity of an asymptomatic case. In sensitivity analyses, we assessed a scenario in which asymptomatic infections did not contribute to pertussis transmission.
Role of adult household contacts in B. pertussis transmission to young infants
According to Van Rie & Hethcote the proportion of infants infected via their parents was one of the key parameters to which the model estimates of the impact of the cocoon strategy was highly sensitive [Reference Hethcote7, Reference Van Rie and Hethcote8]. The proportion of childhood pertussis cases due to transmission from an adult household member was based on data from a recent study involving infants aged 0–5 months [Reference Wendelboe10], and on surveillance data (RENACOQ) [Reference Baron15] for older age groups (Table 3). A conservative estimate of household transmission was made by considering all households evaluated instead of calculating the proportion solely on cases with a known source of infection. Hence there was a disparity between the contribution of household contacts to childhood pertussis in this study and the one reported in 2004 (Table 3) [Reference Van Rie and Hethcote8].
Table 3. Contribution of household members to pertussis transmission according to age

Demographics
Demographic information was updated using data from recent US surveys on age-specific mortality and life expectancy (http://www.cdc.gov/nchs/products/pubs/pubd/lftbls/lftbls.htm), and population size and fertility rates (http://www.census.gov/population/www/index.html). We also relaxed the assumption of the constant size of the population used in the previous analysis [Reference Van Rie and Hethcote8] and considered instead an exponential growth as described notably in Hethcote [Reference Hethcote7]. Based on US statistics, we considered a 1·25% annual growth rate that matched the increase in population observed from 1940 to 2005.
In addition to these main updates, we allowed the protection given by the first dose to wane over time and made slight modifications to the age distribution of the adult population while keeping the number of age groups at 50.
Pertussis vaccination strategies
Five vaccination strategies were considered (Table 1): (1) the current US strategy using five doses between ages 2 months and 4–6 years, (2) the current strategy plus routine adolescent vaccination at age 12 years, as per ACIP recommendations of March 2006, (3) current childhood vaccination strategy plus adolescent vaccination and a targeted (cocoon) vaccination of household contacts of newborns, (4) current childhood vaccination strategy plus adolescent vaccination, cocoon vaccination and a single dose of vaccine for adults as per the ACIP recommendation of December 2006, and (5) current childhood vaccination strategy plus adolescent vaccination and routine adult vaccination every 10 years starting at age 20 years. In the case of routine adult strategy, we considered conservatively that the same group of adults instead of a random selection of adults is vaccinated every 10 years.
Sensitivity analyses
Sensitivity analyses were undertaken to determine the impact of changes in estimates of pertussis incidence and vaccine efficacy. The 95% confidence intervals of the source data for pertussis incidence [Reference Ward5, Reference Purdy12–Reference Sutter and Cochi14] and vaccine efficacy [Reference Ward5, Reference Bisgard9] were used to determine scenarios of high and low levels of pertussis incidence and high and low levels of vaccine efficacy. For the sensitivity analysis on vaccine efficacy, we also took into account the uncertainty on the waning of vaccine protection by including the variation of residence time in vaccine-related compartments (worst case: upper bound in efficacy data and high waning; best case: lower bound in efficacy data and low waning). Additional sensitivity analyses included the use of different WAIFW matrices, exclusion of the possibility of transmission from individuals with asymptomatic pertussis, the role of the external reservoir in disease transmission (i.e. pertussis transmission imported from infectives not belonging to the population modelled), age at which the pertussis vaccine dose is given to adults, and changes coverage rates for the cocoon and routine adult strategy.
RESULTS
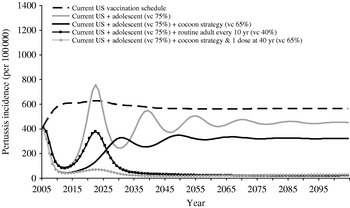
Computer simulations predict that under the current childhood vaccination programme a continued rise in pertussis incidence over the next decade will reach its peak incidence of 628/100 000 in 2022 (Fig. 3). Vaccination of adolescents would substantially reduce the annual number of cases (Fig. 3), reaching incidences as low as 87/100 000 population in 2012. This initial control of pertussis is, however, predicted to be followed by a resurgence of pertussis, with a predicted pertussis incidence of 453/100 000 at steady state, slightly higher compared to the estimated incidence rate in 2005. Adolescent vaccination would have an important direct effect on the annual case load among 10- to 19-year-olds, and a substantial indirect effect on other children, but have no effect on the incidence in adults (Fig. 4).

Fig. 3. Evolution over time of the annual incidence of symptomatic pertussis. vc, Vaccination coverage.

Fig. 4. Annual, age-specific incidence of symptomatic (typical+mild) pertussis cases once steady state situation has been reached. vc, Vaccination coverage.
Adding a targeted cocoon vaccination component to the adolescent vaccination programme would lead to a similar pattern of initial control followed by resurgence, albeit with a lower pertussis incidence at steady state, i.e. 324/100 000 (Fig. 3). The impact of adding the cocoon strategy would be greatest among young children (Fig. 4).
Incorporating either cocoon or routine adult vaccination programmes will initially have little impact but will prevent the re-emergence of pertussis seen upon implementation of adolescent vaccination.
Implementation of the recent ACIP recommendations for adolescents and adults, i.e. adding to the childhood schedule one dose for adolescents, one dose for all adults and vaccinating close contacts of newborns, would lead to large reductions in pertussis incidence rates and sustained control of pertussis in all age groups (Figs 3 and 4).
Adult vaccination: impact of age and vaccination coverage rates
The impact of a single booster of pertussis vaccine for adults depends on the age at which the vaccination is administered (Fig. 5). The model predicts that, when this booster dose complements the cocoon strategy, the optimal age is 40 years.

Fig. 5. Impact of the age of adult booster dose of pertussis vaccine on the annual pertussis incidence and on the annual number of vaccinations needed.
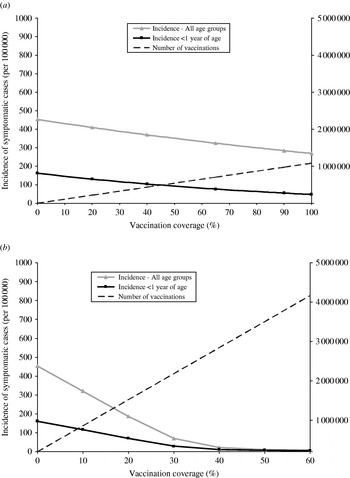
The impact of the cocoon strategy increases with the increasing proportion of parents of newborn infants vaccinated (Fig. 6a). However, even if all parents are vaccinated, the cocoon strategy can not reduce pertussis incidence among infants aged <1 year to the level achieved in the strategy where a single routine adult booster is added to the cocoon strategy (incidence of 37 and 10/100 000 infants, respectively).

Fig. 6. Impact of vaccination coverage rate on annual pertussis incidence and annual number of vaccinations by adult vaccination strategy. (a) Childhood+adolescent+cocoon strategy. (b) Childhood+adolescent+routine adult every 10 years.
The greatest impact of the strategy that requires the vaccination of all adults every 10 years is achieved for coverage rates of 10–40% (Fig. 6b), with any increase of vaccination coverage having a minimal impact on pertussis incidence.
Although routine vaccination of adults every 10 years is predicted to lead to the largest reductions in pertussis incidence, the total number of vaccine doses needed is considerably greater (Figs 5 and 6). Overall the cocoon strategy plus a single dose for adults has a stronger impact on pertussis incidence for an equivalent number of vaccinations administered. For example, the number of additional doses required by the implementation of the cocoon strategy and a single dose for adults in the base case is similar to the number of doses required for a 22% coverage of the routine adult vaccination strategy every 10 years, and ultimately leads to a lower incidence: 33 vs. 161/100 000 population.
Sensitivity analyses
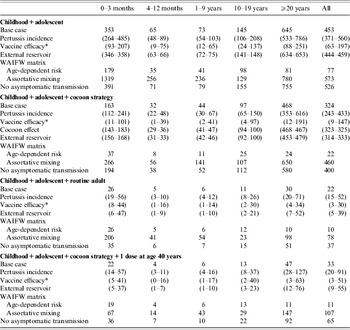
The sensitivity analyses did not change the ranking of the different strategies with respect to their impact on pertussis incidence (Table 4). While the variation of some of the parameters had a limited (cocoon effect, external reservoir) to moderate (pertussis incidence) impact, the variation of others had a more marked influence on model results. For instance, considering the best case for vaccine efficacy leads to a similarly low incidence for both routine adult vaccination and single-dose adult vaccination in addition to the cocoon strategy. Assuming that the transmission rate depends only on the age of infected individuals (i.e. no specific mixing within and between any age groups), also limits the value of extending the vaccination strategy beyond cocoon and single dose for adults. Finally, excluding the potential of transmission from individuals with asymptomatic infection had only a limited impact on model predictions.
Table 4. Sensitivity analyses: the impact of changes in pertussis incidence, vaccine efficacy, cocoon effect and contact matrix on the age-specific incidence of symptomatic (typical+mild) pertussis, according to adult immunization strategy

* As measured in Bisgard et al. [Reference Bisgard9] and Ward et al. [Reference Ward5] and with extreme values for residence time in vaccine-related compartments.
WAIFW, Who acquires infection from whom.
DISCUSSION
The analysis performed predicts that implementation of the 2006 ACIP recommendations for adolescent and adult pertussis vaccination will lead to sustained control of pertussis in the United States [Reference Broder3]. Implementing the adolescent vaccination strategy alone, or the combination of routine adolescent and targeted adult vaccination without a routine booster for adults is predicted to result in an initial decrease in pertussis incidence, that is followed by a re-emergence of pertussis a few decades later, similar to what was experienced after the introduction of childhood pertussis immunization. According to the model predictions, both the combination of the cocoon strategy and a single dose for all adults and a decennial routine adult vaccination can be highly effective in further reducing the burden of disease among US infants, adolescents and adults.
Routine adult vaccination may have the greatest impact on pertussis incidence in all age groups, but the health-care resources needed to implement a nationwide, routine adult vaccination programme effectively are probably higher than those required for a single dose for all adults in addition to vaccination of close contacts of newborns.
In the current study, we showed that in the base case, a 40% coverage for routine adult vaccination would be sufficient to reduce overall pertussis incidence to a few cases per 100 000 person-years. In general, vaccination programmes rely on high levels of coverage to achieve success. The finding that a relatively low coverage rate for routine adult vaccination could be highly effective for the control of pertussis in the United States is promising, particularly considering the existence of the current adult tetanus and diphtheria vaccination programme infrastructure. It should be noted that these outcomes required that a high coverage is maintained for children and obtained for adolescents.
A prior mathematical modelling study of adult pertussis vaccination [Reference Van Rie and Hethcote8] also concluded that routine adult vaccination would be more effective than the cocoon strategy, but differed in some important predictions. Van Rie & Hethcote predicted that the cocoon strategy would have a greater impact than routine vaccination on disease incidence among infants, and that routine adult vaccination would reduce the overall pertussis incidence by 25% relative to childhood plus adolescent vaccination, whereas we determined that a 40% coverage would reduced pertussis incidence by more than 95%. The main sources of these differences can be explained by differences in key parameters: baseline pertussis incidence among adults, vaccine effectiveness and the calculated forces of infection. Van Rie & Hethcote used force-of-infection data from the pre-vaccination era in England, corresponding to a pertussis incidence in the base case of 878 cases/100 000 person-years. Recent data allowed us to calculate forces of infection using incidence estimates of 350 cases/100 000 person-years, in 2004 [Reference Ward5]. In addition, the effectiveness per dose differed between the two studies: previously, effectiveness levels of 19%, 67·6%, 76·1% and 82·4% after the first, second, third and fourth dose, respectively, were used, whereas we used levels of 46%, 79·6%, 91·7% and 96·4%, respectively, based on the results of a recent case-controlled vaccine effectiveness study [Reference Bisgard9].
The study by Van Rie & Hethcote also demonstrated that the proportion of infants infected by adult household contact was one of the key parameters to which the model was highly sensitive. Using data from a recent prospective study designed to identify the sources of infant pertussis infection [Reference Wendelboe10] and including data on all infants instead of selected data from households where the source of infection was known, we obtained more conservative figures for the cocoon effect and results that were less sensitive to changes in assumptions on the cocoon strategy. The differences in results obtained using data from different sources highlights the need to evaluate and re-evaluate model predictions whenever important new data become available.
Several limitations to the present study should be noted. First, even though the data presented here were derived using data from recently published sources [Reference Ward5, Reference Bisgard9, Reference Wendelboe10], there were limitations to these source data such as the low precision of the estimates of pertussis incidence and vaccine effectiveness as indicated by the wide confidence intervals. Data reported by Bisgard et al. [Reference Bisgard16] is another illustration of the important differences in reported incidence despite those data exclusively referring to states having implemented an enhanced surveillance system. Parameter estimates are likely to be further refined in the future and changes may occur as the incidence of pertussis varies temporally and geographically. However, a certain level of uncertainty will always remain which can only be addressed by the extensive use of sensitivity analyses.
Second, the sensitivity analyses performed on the structure of the WAIFW matrix also impacts model results: the more pertussis transmission is characterized by higher levels of contacts between some groups of individuals (assortative case and base case compared to age-dependent risk), the more adult vaccination is necessary for pertussis control. The difficulty in obtaining an accurate estimate of differences in the level of contacts therefore limits model predictions.
Third, it should be noted that although we have compared the impact of two adult vaccination strategies by the number of dosages needed, we have not undertaken a detailed economic evaluation. Economic evaluations have been performed by others [Reference Caro17, Reference Lee18] but the conclusions were limited as the authors did not use a transmission model, limiting their evaluations to the direct effect of vaccination strategies. An economic evaluation, using epidemiological results reported here would be the next step in the assessment of the value of adult vaccination pertussis strategies.
In conclusion, the results of this computer simulation, which took into account the most recent data on the epidemiology of pertussis in the United States and new data on pertussis vaccine effectiveness, show that a combination of childhood, adolescent and adult vaccination strategy is necessary to maintain a high level of pertussis infection control in the United States. The model simulations thus supports the recent ACIP guidelines of combining routine adolescent vaccination, with targeted vaccination of close contacts of infants and a booster dose for all adults to be administered preferably at 40 years of age.
ACKNOWLEDGEMENTS
We thank the two anonymous referees for their valuable comments that helped us improve the manuscript. This study was supported by Sanofi Pasteur.
DECLARATION OF INTEREST
L. Coudeville and P. Andre are employees of Sanofi Pasteur.
APPENDIX 1
Mathematical description of the model
Equations for transition from or to a state of full susceptibility regarding pertussis (S) are defined as follows

f and P(t) correspond respectively to the fertility rate and population size. fP(t) gives the number of births at date t. μi, is the mortality rate in age class i. A i, is the transition rate to the upper age class (l i stands for the length of age class i and q for the growth rate of the population):
λi(t) stands for the force of infection (see below for its calculation). sevjs is the probability, for fully susceptible individuals, that risk exposure leads to respectively a typical pertussis case (j=1), a mild pertussis case (j=2) or an asymptomatic pertussis case (j=3). Cocoon is the proportion of newborns benefiting from the cocoon effect (cocoon=0 if this strategy is not implemented). coci is the proportion of contaminations not covered by the cocoon effect in age class i. Cocoon effect is limited to children aged <5 years (∀i>10, coci=1).
Equations for individuals benefiting from the protection associated to 1 or 2 vaccine doses (V1–V2) are defined as follows:

The effect of the third vaccine dose differs in the model according to the age at which it is administered. For children up to 1 year of age (i⩽5), equations corresponding to the administration of 3 or 4 doses are therefore given by:

Above 1 year of age (i>5) an additional vaccine dose for individuals having 2 or 3 doses is assumed to identically lead to full vaccine protection (V4):

WV1–WV3 used in the equations above corresponds to a partial waning of vaccine-induced immunity. Equations for these state variables are given by:

Differential equations for infectious individuals (Y1–Y3), immune individuals (R) and individuals having partially lost their natural immunity (WN1–WN3) are similar to those benefiting and not benefiting from the cocoon effect. Therefore, for simplicity purposes, we are only presenting equations corresponding to individuals not benefiting from the cocoon effect.

In the above equations, 1/σi refers to the average duration of the infectious period according to the level of pertussis severity and CA i,j(t) is the number of new infections in age group i of type j at time t. This variable is defined by:

Equations for immune individuals are given by:

Equations for individuals having partially lost their natural immunity against pertussis are given by:

The force of infection is given by:
τi stands for the relative infectivity of typical, mild and asymptomatic pertussis. βi, j is the transmission rate from an individual of age group j to an individual of age group j. λ0 stands for virus transmission from an external reservoir (i.e. pertussis transmission from infectives not belonging to the population). Finally, P(t) is the size of the population at date t.
It should also be mentioned that in order to model the routine adult strategy, we split the adult population between vaccinated and unvaccinated by creating specific compartments for each subgroup.
APPENDIX 2
Calibration procedure
The three-set of parameters (age-specific transmission rates, vaccine-related parameters and relative infectivity of asymptomatic infections) were calibrated simultaneously. The calibration procedure was therefore repeated until the conditions for defining an optimal solution was obtained simultaneously for the three-set of parameters.
Age-specific transmission rates
To perform this calibration, we used a model similar to one previously used in the case of measles [Reference Coudeville19]. This method is based on an expectation-minimization algorithm, i.e. a two-stage process repeated until convergence.
• The expectation stage consists in extrapolating the age-specific force of infection (λie) and the number of infectives rescaled to fit with a population size set to 1 (Y1ie, Y2ie, Y3ie) for the period for which data are available. This is based on observed data (age-specific incidence) but also on initial values for the parameters to be estimated (age-specific transmission rates) and is done by running the model starting from the pre-vaccination period. For the period with observed data, the daily number of symptomatic cases is calculated using incidence data as well as the evolution over time of the number of cases derived from the initial values of the age-specific transmission rates. These daily cases can further be used to determine the daily values of λie, Y1ie, Y2ie, Y3ie since for a short period of time the force of infection can be assumed to remain stable. The value of λie, Y1ie, Y2ie, Y3ie for the entire period of observation is simply given by the aggregation of daily values.
• The minimization stage is in fact here a calculation stage since calibration is performed with one set of age-specific incidence data. It consists in solving the following equation to get the age-specific transmission rates (βi, j)

The βi, j obtained by solving the above equation then become the initial values for the next iteration of the EM algorithm. Convergence is considered as reached when the difference between the expected age-specific incidences and those derived from the βi, j values do not exceed 10−5 in any age group.
It should be mentioned that when only λie, Y1ie, Y2ie, Y3ie are known the above equation remains under-identified. Solving it requires at first ι1, ι2, ι3, λ0 to be known. ι1, ι2, ι3 is in fact the result of the estimate of the contribution of asymptomatic to disease transmission. λ0 which represents virus transmission from an external reservoir, is set at a very low value (5×10−5 in the base case), ranging from 10−4 to 10−5 in sensitivity analyses.
Solving this equation also requires putting constraints on the βi, j through the use of a specific matrix form, usually WAIFW matrices. Considering age groups for which we were able to derive age-specific incidence, the population was divided in the WAIFW matrices into eight age groups: 0–5 months, 6–11 months, 1–4 years, 5–9 years, 10–19 years, 20–29 years, 30–39 years, ⩾40 years.
We used in the base case a WAIFW matrix structure similar to the one considered in Van Rie & Hethcote [Reference Van Rie and Hethcote8].
![\openup1\eqalign{\tab\openup-6 \scale75%\matrix{ {0 \mbox{-} 5} \tab {6 \mbox{-} 11} \tab {1 \mbox{-} 4} \tab {5 \mbox{-} 9} \tab {10 \mbox{-} 19} \tab {20 \mbox{-} 29} \tab {30 \mbox{-} 39} \tab {\ges 40} \cr {{\rm mo}{\rm.}} \tab {{\rm mo}{\rm.}} \tab {{\rm yr}} \tab {{\rm yr}} \tab {{\rm yr}} \tab {{\rm yr}} \tab {{\rm yr}} \tab {{\rm yr}} \cr} \cr \tab\!\! \left[ {\matrix{ {\;\beta _{\setnum{1}} } \tab {\;\beta _{\setnum{1}} } \tab {\;\beta _{\setnum{1}} } \tab {\;\beta _{\setnum{1}} } \tab {\;\beta _{\setnum{1}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \cr {\beta _{\setnum{1}} } \tab {\beta _{\setnum{2}} } \tab {\beta _{\setnum{2}} } \tab {\beta _{\setnum{2}} } \tab {\beta _{\setnum{2}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \cr {\beta _{\setnum{1}} } \tab {\beta _{\setnum{2}} } \tab {\beta _{\setnum{3}} } \tab {\beta _{\setnum{3}} } \tab {\beta _{\setnum{3}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \cr {\beta _{\setnum{1}} } \tab {\beta _{\setnum{2}} } \tab {\beta _{\setnum{3}} } \tab {\beta _{\setnum{4}} } \tab {\beta _{\setnum{3}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \cr {\beta _{\setnum{1}} } \tab {\beta _{\setnum{2}} } \tab {\beta _{\setnum{3}} } \tab {\beta _{\setnum{3}} } \tab {\beta _{\setnum{5}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \cr {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \cr {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{7}} } \tab {\;\;\;\beta _{\setnum{7}} } \cr {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{6}} } \tab {\;\;\;\beta _{\setnum{7}} } \tab {\;\;\;\beta _{\setnum{8}} } \cr} } \right] \cr}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151016064148377-0322:S0950268807009041_eqnU14.gif?pub-status=live)
In sensitivity analyses, we also considered WAIFW matrices characterized by respectively, assortative mixing and age-dependent transmission rates.
![\eqalign{\tab\openup-6 \scale64%\matrix{\hskip4 {0 \mbox{-} 5} \tab {6 \mbox{-} 11} \tab {1 \mbox{-} 4} \tab {5 \mbox{-} 9} \tab {10 \mbox{-} 19} \tab {20 \mbox{-} 19} \tab {30 \mbox{-} 19} \tab {\ges 40} \cr\hskip4 {{\rm mo}{\rm.}} \tab {{\rm mo}{\rm.}} \tab {{\rm yr}} \tab {{\rm yr}} \tab {{\rm yr}} \tab {{\rm yr}} \tab {{\rm yr}} \tab {{\rm yr}} \cr} \quad\quad\quad\hskip4 \scale64%\matrix { {0 \mbox{-} 5} \tab {6 \mbox{-} 11} \tab {1 \mbox{-} 4} \tab {5 \mbox{-} 9} \tab {10 \mbox{-} 19} \tab {20 \mbox{-} 19} \tab {30 \mbox{-} 19} \tab {\ges 40} \cr {{\rm mo}{\rm.}} \tab {{\rm mo}{\rm.}} \tab {{\rm yr}} \tab {{\rm yr}} \tab {{\rm yr}} \tab {{\rm yr}} \tab {{\rm yr}} \tab {{\rm yr}} \cr} \cr \tab \left[ {\matrix{ {\beta _{\setnum{1}} } \tab {\beta _{\setnum{1}} } \tab {\beta _{\setnum{1}} } \tab {\beta _{\setnum{1}} } \tab {\beta _{\setnum{1}} } \tab {\beta _{\setnum{1}} } \tab {\,\,\beta _{\setnum{1}} } \tab {\,\beta _{\setnum{1}} } \cr {\beta _{\setnum{2}} } \tab {\beta _{\setnum{2}} } \tab {\beta _{\setnum{2}} } \tab {\beta _{\setnum{2}} } \tab {\beta _{\setnum{2}} } \tab {\beta _{\setnum{2}} } \tab {\beta _{\setnum{2}} } \tab {\beta _{\setnum{2}} } \cr {\beta _{\setnum{3}} } \tab {\beta _{\setnum{3}} } \tab {\beta _{\setnum{3}} } \tab {\beta _{\setnum{3}} } \tab {\beta _{\setnum{3}} } \tab {\beta _{\setnum{3}} } \tab {\beta _{\setnum{3}} } \tab {\beta _{\setnum{3}} } \cr {\beta _{\setnum{4}} } \tab {\beta _{\setnum{4}} } \tab {\beta _{\setnum{4}} } \tab {\beta _{\setnum{4}} } \tab {\beta _{\setnum{4}} } \tab {\beta _{\setnum{4}} } \tab {\beta _{\setnum{4}} } \tab {\beta _{\setnum{4}} } \cr {\beta _{\setnum{5}} } \tab {\beta _{\setnum{5}} } \tab {\beta _{\setnum{5}} } \tab {\beta _{\setnum{5}} } \tab {\beta _{\setnum{5}} } \tab {\beta _{\setnum{5}} } \tab {\beta _{\setnum{5}} } \tab {\beta _{\setnum{5}} } \cr {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{6}} } \cr {\beta _{\setnum{7}} } \tab {\beta _{\setnum{7}} } \tab {\beta _{\setnum{7}} } \tab {\beta _{\setnum{7}} } \tab {\beta _{\setnum{7}} } \tab {\beta _{\setnum{7}} } \tab {\beta _{\setnum{7}} } \tab {\beta _{\setnum{7}} } \cr {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \cr} } \right]\quad \quad \quad \left[ {\matrix{ {\beta _{\setnum{1}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\,\,\beta _{\setnum{8}} } \tab {\,\beta _{\setnum{8}} } \cr {\beta _{\setnum{8}} } \tab {\beta _{\setnum{2}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \cr {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{3}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \cr {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{4}} } \tab {\beta _{\setnum{7}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \cr {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \cr {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{6}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \cr {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{7}} } \tab {\beta _{\setnum{8}} } \cr {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \tab {\beta _{\setnum{8}} } \cr} } \right] \cr \tab \cr}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary-alt:20160705010251-31199-mediumThumb-S0950268807009041_eqnU15.jpg?pub-status=live)
Vaccine-related parameters
Available vaccine efficacy data give an estimate of the direct effects of vaccination. Assessing only direct effects with the model can be done by eliminating the impact of vaccination on the force of infection. To calculate vaccine efficacy, we therefore compared several scenarios using the same force of infection for each of them, i.e. the one estimated from US incidence data. More specifically, we calculated the percentage reduction in the number of cases when the whole population receives the first, second, third or the fourth dose, respectively, using as a reference the ‘no vaccination’ scenario. For example, if ![]() and
and ![]() are defined respectively as the number of symptomatic cases in a situation where the force of infection matches recent US incidence data, and nobody is vaccinated or everybody receives the first dose, vaccine efficacy for the first dose is given by:
are defined respectively as the number of symptomatic cases in a situation where the force of infection matches recent US incidence data, and nobody is vaccinated or everybody receives the first dose, vaccine efficacy for the first dose is given by:
To adjust vaccine-related parameters, we considered the existence of a latent variable for severity of pertussis infection and associated to it a normal distribution. For symptomatic infections, this severity variable was characterized by the duration of cough (a severity >3 meaning typical infection, a severity between 0 and 3 meaning mild infection). The mean (m S) and standard deviation (d S) of this normal distribution were therefore identified using the probability of fully susceptibles to develop a typical (73%) or mild (25%) infection defined in Van Rie & Hethcote [Reference Van Rie and Hethcote8]. This led to m S=4·325 and d S=2·183.
Vaccination helps the organism in fighting the virus and limiting the consequences of an infection. This was translated in the model by a shift towards left in the distribution of severity in the case of an infection, i.e. a decrease in the mean of severity distribution. For each of the vaccine-related compartments, we therefore estimated a specific decrease of the mean of severity distribution. The estimate performed in the base case led to V1–V4 and WV1–WV3 to decrease to 4·7, 6·58, 7·46, 8·64, 0, 4·935, 7·46, respectively.
The probability of developing typical, mild or asymptomatic cases for vaccine-related compartments, presented Table 2, is a direct consequence of this estimation. For instance, if &Xtilde; follows a standard normal distribution, the probability of developing a typical case for an individual in compartment V1 is given by:
Relative infectivity of asymptomatic infections
Relative infectivity of asymptomatic infections (τ3) was adjusted to reproduce the contribution of asymptomatic infections (16%) in the transmission of pertussis to infants as reported in Wendelboe et al. [Reference Wendelboe10]. For symptomatic cases (mild and typical), as in Van Rie & Hethcote [Reference Van Rie and Hethcote8], the value of relative infectivity is 1.
In the model, the contribution of asymptomatic infection to disease transmission can be measured through the following expression:
The estimation performed led to τ3=0·915 in the base case.