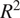Impact Statement
This paper discusses the use of novel developments in the machine-learning field in seasonal forecasting. Traditionally, climate models are used to simulate physical, chemical and biological processes in the atmosphere to generate climate projections. Machine-learning methods are gaining popularity in different fields. A team of computer scientists and earth scientists worked on this paper that investigates the use of machine-learning algorithms along with climate models for seasonal forecasts, which are critical for better resource management.
1. Introduction
Seasonal forecast is defined as a variety of potential climate changes that are likely to occur in the coming months and seasons (Pan et al., Reference Pan, Anderson, Goncalves, Lucas, Bonfils and Lee2022). This is crucial for governments and decision makers to better manage natural resources such as water, energy, and agriculture, as well as protect human health (Yuan et al., Reference Yuan, Huang and Duan2019; Talukder et al., Reference Talukder, Ganguli, Matthew, vanLoon, Hipel and Orbinski2021). For example, crop producers use seasonal forecasts to make decisions about the timing of planting and harvesting, field fertilization and water management (Klemm and McPherson, Reference Klemm and McPherson2017). Weather plays an important role in energy supply and demand (Felice et al., Reference Felice, Alessandri and Catalano2015); hence, an accurate forecast of future weather conditions could increase the effectiveness and dependability of energy management at the local and national levels given the requirement to maintain the balance between electricity production and demand. Accurate forecasting of extreme events such as storms, heatwaves, droughts and floods is required to improve disaster preparedness (Liu et al., Reference Liu, Huang, Xiao and Tong2022).
Weather prediction at shorter timescales such as daily to monthly depends on the understanding of physical processes in the atmosphere as well as interactions among the atmosphere, oceans and land. An important distinction must be made between dynamical predictions, which use intricate physical numerical models and statistical predictions, that use regional historical relationships between physical variables like temperature and precipitation (Roads et al., Reference Roads, Chen and Kanamitsu2003; Lorenzoni and Pidgeon, Reference Lorenzoni and Pidgeon2006; Troccoli, Reference Troccoli2010; Klemm and McPherson, Reference Klemm and McPherson2017; Franzke et al., Reference Franzke, Blender, O’Kane and Lembo2022). Two approaches for constraining climate predictions based on past climate change include large ensembles of simulations from computationally efficient models and small ensembles of simulations from state-of-the-art coupled ocean–atmosphere General Circulation Models (GCMs; Stott and Forest, Reference Stott and Forest2007). GCMs are frequently used in studies related to the impacts of large-scale climate change (Fujihara et al., Reference Fujihara, Tanaka, Watanabe, Nagano and Kojiri2008). High-resolution climate data from current global climate models are provided using Regional Climate Downscaling (RCD) techniques (Laprise, Reference Laprise2008; Scinocca et al., Reference Scinocca, Kharin, Jiao, Qian, Lazare, Solheim and Flato2016). Several programs such as THORPEX, DEMETER and EUPORIAS have been launched in practice to work toward seasonal forecasting (Toth et al., Reference Toth, Pena and Vintzileso2007; Klemm and McPherson, Reference Klemm and McPherson2017).
In 1995, Coupled Model Intercomparison Projects (CMIP) began as a comparison of a few pioneering global coupled climate models and their outputs are used by different organizations around the world, such as the IPCC to better understand past, present, and future climate change (Wang et al., Reference Wang, Liu, Shao, Mei, Su and Wang2021; Xu et al., Reference Xu, Han, Tam, Yang and Fu2021; Liu et al., Reference Liu, Huang, Xiao and Tong2022). CMIP6 is the most recent phase of the CMIP. The CMIP6 platform, which began in 2015, offers the most up-to-date multi-model datasets. Simulation outputs from more than 100 different climate models produced by more than 50 different modeling groups contributed to CMIP6. In addition to historical studies, seasonal forecasts for different emission scenarios are provided (Fan et al., Reference Fan, Duan, Shen, Wu and Xing2020; Turnock et al., Reference Turnock, Allen, Andrews, Bauer, Deushi, Emmons, Good, Horowitz, John, Michou, Nabat, Naik, Neubauer, O’Connor, Olivié, Oshima, Schulz, Sellar, Shim, Takemura, Tilmes, Tsigaridis, Wu and Zhang2020; Zhang and Li, Reference Zhang and Li2021; Liu et al., Reference Liu, Huang, Xiao and Tong2022).
In recent years, big data, effective supercomputers with graphics processing units (GPUs), and scientific interest in novel algorithms and optimization techniques proved to be significant turning points in machine-learning history. Machine learning has recently been a hot topic in climate studies. Tyagi et al. (Reference Tyagi, Zhang, Saraswat, Sahany, Mishra and Niyogi2022) reviewed a number of studies that applied the different machine-learning/deep-learning algorithms in flash drought (FD) studies. Luo et al. (Reference Luo, Nadiga, Park, Ren, Xu and Yoo2022) used a Bayesian deep-learning approach to near-term climate prediction in the North Atlantic. Bochenek and Ustrnul (Reference Bochenek and Ustrnul2022) investigated the top 500 scientific articles about machine learning in the field of climate and numerical weather prediction that have been published since 2018. Anochi et al. (Reference Anochi, de Almeida and de Campos Velho2021) evaluated different machine-learning methods for precipitation prediction in South America. Zhang and Li (Reference Zhang and Li2021) and Feng et al. (Reference Feng, Wang, Wei, Amankwah, Hu, Luo, Hagan and Ullah2022) used deep-learning algorithms to downscale hydroclimatic data of CMIP6 simulations in China.
This study aimed to improve seasonal temperature forecasts using both climate models and machine-learning algorithms. Specifically, the objective was to utilize the power of CMIP6 physical models along with the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis 5th Generation (ERA5) dataset (created using data assimilation and model forecasts) while utilizing specifically deep neural network-learning methods for a better global seasonal forecast of 2 m temperature.
2. Materials and Methods
2.1. Training data
This study has utilized the monthly averaged meteorological parameters (i.e., 2 m temperature, 10 m eastward component of wind, 10 m northward component of wind, geopotential height at 500 hPa, mean sea-level pressure, and precipitation flux) from nine fully coupled Earth System Models (ESM) that participated in the CMIP6 (Eyring et al., Reference Eyring, Bony, Meehl, Senior, Stevens, Stouffer and Taylor2016). These models are ACCESS-CM2, CNRM-CM6–1-HR, GISS-E2–1-H, NorESM2-MM, CESM2-WACCM, EC-Earth3-Veg, MPI-ESM1–2-HR, MIROC-ES2L, and IPSL-CM6A-LR. For each ESM model, only one ensemble member was used and the time slice for the coupled models is chosen from the historical period (i.e., from year 1850 to 2014). For each ensemble, 1,700 data instances are separated for training and 100 instances for testing.
For validation and fine-tuning, monthly averaged 2 m temperature data from the ERA5 reanalysis dataset Copernicus Climate Change Service (C3S) (2017) have been used. The ERA5 dataset is partitioned into two different time slices: years 1973–2016 (400 samples) are used for fine-tuning, while years 2016–2021 (116 samples) are used for evaluation of the trained models. In order to estimate the performance of the deep-learning model (which is called as AI model from now on) between 2016 and 2021, we also used the multi-model mean of the CMIP6 models using the IPCC SSP5–8.5 scenario which is selected since there was no significant reduction in carbon emissions after 2014 when the historical simulations ended.
2.2. Model architecture
As this study focuses on spatiotemporally varying data, an encoder–decoder-based architecture UNet++ (Zhou et al., Reference Zhou, Md Siddiquee, Tajbakhsh and Liang2018), which is based on the original UNet architecture (Ronneberger et al., Reference Ronneberger, Fischer and Brox2015) is adapted. In UNet++, the skip connections of the UNet are re-designed to minimize the semantic gap between the feature maps coming from the sub-networks of the encoder and the decoder, making the learning easier. Our model specifically employs convolutional neural network (CNN) layers due to the nature of the input data. We construct the UNet++ in order to perform a prediction task, which is explained below. The architecture includes a contracting path, that is, an encoder part, which summarizes the information by reducing the size of the input image and increasing the number of channels. This downsampling operation results in spatial information loss due to the compression of the input. The UNet++, as in the original UNet, introduces skip connections that reduce the information loss after the bottleneck layer and recovers fine-grained details. Skip connections aggregate information from different resolution levels in order to increase accuracy and speed up the convergence. In the expansive path, that is, the decoder part, skip connections concatenate the outputs of each downsampling layer to corresponding upsampling layers, aiming at image reconstruction that is at the same spatial resolution as that of the input. In addition to UNet++, by training several state-of-the-art CNN architectures a benchmark has been created. As the baseline model, the classical CNN architecture ResNet is used. Furthermore, similar to UNet++, results of the other segmentation models such as DeepLabV3 Chen et al. (Reference Chen, George, Florian and Adam2017) and PSPNet Zhao et al. (Reference Zhao, Shi, Qi, Wang and Jia2017) are included in the benchmark.
Figure 1a depicts the block diagram of the neural network model that we construct for the seasonal forecast of temperature. In addition to 2 m temperature, an elevation map is stacked to the input as ancillary data to investigate whether it can improve the prediction performance. Along with elevation and temperature data, experiments are done by stacking more climate variables per month such as u10 (10 m eastward component of wind), v10 (10 m northward component of wind), zg500 (Geopotential height at 500 hPa), psl (mean sea-level pressure) and pr (precipitation flux) and giving into the network. We use two different experimental settings to evaluate the effectiveness of using fully historical input data versus periodic data. The first setting is designed to see the performance of the historical data stacked sequentially in a temporal manner such as from
![]() $ t-1 $
to
$ t-1 $
to
![]() $ t-6 $
,
$ t-6 $
,
![]() $ t-12 $
and up to
$ t-12 $
and up to
![]() $ t-36 $
. However in the second set, the target month and its neighbors are stacked in a yearly manner from historical data to assess the effect of periodicity. Months before the target prediction, the previous years’ target month and months before and after them (e. g. neighboring months) are stacked as the input. The number of previous lag years as well as the number of preceding and succeeding months are selected as hyper-parameters. We have explored lag years 1 to 4 and preceding/succeeding 1 and 2 months. Two examples for these settings are given in 1b. The input to the Encoder network consists of the maps (temperature and elevation) corresponding to the month
$ t-36 $
. However in the second set, the target month and its neighbors are stacked in a yearly manner from historical data to assess the effect of periodicity. Months before the target prediction, the previous years’ target month and months before and after them (e. g. neighboring months) are stacked as the input. The number of previous lag years as well as the number of preceding and succeeding months are selected as hyper-parameters. We have explored lag years 1 to 4 and preceding/succeeding 1 and 2 months. Two examples for these settings are given in 1b. The input to the Encoder network consists of the maps (temperature and elevation) corresponding to the month
![]() $ t-1 $
, which is one previous to the target month
$ t-1 $
, which is one previous to the target month
![]() $ t $
,
$ t $
,
![]() $ t-12\pm \Delta t $
,
$ t-12\pm \Delta t $
,
![]() $ t-24\pm \Delta t $
, and
$ t-24\pm \Delta t $
, and
![]() $ t-36\pm \Delta t $
, where
$ t-36\pm \Delta t $
, where
![]() $ \Delta t $
could be either one of
$ \Delta t $
could be either one of
![]() $ \left\{1,2\right\} $
. Specifically, we selected
$ \left\{1,2\right\} $
. Specifically, we selected
![]() $ \Delta t=2 $
in order to account for possible seasonal monthly shifts. The overall concatenated input tensor goes through the UNet++ model, and a single prediction map for temperature at the target month
$ \Delta t=2 $
in order to account for possible seasonal monthly shifts. The overall concatenated input tensor goes through the UNet++ model, and a single prediction map for temperature at the target month
![]() $ t $
is produced at the output of the network, as visualized in Figure 1a. A total of 6 different AI models were developed when investigating the UNet and its successor the UNet++ with ERA5 fine-tuning. Considering all hyper-parameters (i.e., sequential and nonsequential), we have designed 14 experimental settings (named as cases from now on) resulting in 84 simulations in total. It should be noted that we also explored going back to lag years from 5 to 10, however as the number of lag years are increased, the amount of validation data is naturally decreased, and as a result, the data size was not adequate for the model optimization process. Therefore, we have stopped at year 4 for model setup.
$ t $
is produced at the output of the network, as visualized in Figure 1a. A total of 6 different AI models were developed when investigating the UNet and its successor the UNet++ with ERA5 fine-tuning. Considering all hyper-parameters (i.e., sequential and nonsequential), we have designed 14 experimental settings (named as cases from now on) resulting in 84 simulations in total. It should be noted that we also explored going back to lag years from 5 to 10, however as the number of lag years are increased, the amount of validation data is naturally decreased, and as a result, the data size was not adequate for the model optimization process. Therefore, we have stopped at year 4 for model setup.

Figure 1. (a) Depiction of the UNet++ model which we adapted to our seasonal temperature forecast task. Month descriptions in the input of the encoder refer to relative timing of the input channels (e.g., each month used) according to the target month. In addition to input months, an elevation map is added as a separate channel. (b) Arrangement of the months for the multi-dimensional input for the experimental settings: (a) 2 years 1 months (given in the first row), and (b) 2 years 2 months (given in the second row) are shown.
As the spherical earth in 3D (3-dimensions) is represented over a 2D spatial grid, one has to pay attention to the spatial information at the edges of images while applying convolutions. Rather than traditional 3 × 3 spatial convolutions, 3 × 3 circular convolutions that pad the input with information from the opposite sides of the image are used to preserve the spatial information at the edges of the image. During downsampling, three maxpool operations and eight convolutional layers with batch normalization are used. Similarly, the upsampling path is designed using three upsample and seven convolutional layers with batch normalization. As UNet++ introduces intermediate feature maps for the skip connections in each level during downsampling and upsampling, six convolutional layers are used for constructing all the intermediate feature maps. Moreover, concatenating lower-resolution feature maps requires the usage of three additional upsample layers. For training the neural network model, as the loss function, the mean squared error (MSE) loss in (1) is utilized:
 $$ L\left(\theta \right)=\frac{1}{N}\sum \limits_{i=1}^N{\left(\hskip0.2em {f}_{\theta}\left({X}_i\right)-{Y}_i\right)}^2, $$
$$ L\left(\theta \right)=\frac{1}{N}\sum \limits_{i=1}^N{\left(\hskip0.2em {f}_{\theta}\left({X}_i\right)-{Y}_i\right)}^2, $$
where
![]() $ {f}_{\theta } $
represents the neural network model,
$ {f}_{\theta } $
represents the neural network model,
![]() $ {X}_i $
is the input multichannel tensor consisting of stacked monthly data and elevation data,
$ {X}_i $
is the input multichannel tensor consisting of stacked monthly data and elevation data,
![]() $ {Y}_i $
is the target temperature in the grid (“Ground Truth”), and N corresponds to the number of target time steps in a given batch of the selected stochastic gradient descent optimizer.
$ {Y}_i $
is the target temperature in the grid (“Ground Truth”), and N corresponds to the number of target time steps in a given batch of the selected stochastic gradient descent optimizer.
2.3. Training and evaluation
After the neural network model is constructed, it is trained with the MSE loss function in all experiments. A learning rate of
![]() $ 1e-5 $
and a weight decay of
$ 1e-5 $
and a weight decay of
![]() $ 1e-3 $
are used with a step learning rate scheduler with Adam optimizer Kingma and Ba (Reference Kingma and Ba2015). The model is optimized for 40 epochs and early stopping is used to avoid over-fitting. After each convolutional layer, a batch normalization layer is used. The batch size is chosen as 16. The training process is performed on an NVIDIA RTX A5000 GPU and the results are delivered on average after 3–4 hr of training.
$ 1e-3 $
are used with a step learning rate scheduler with Adam optimizer Kingma and Ba (Reference Kingma and Ba2015). The model is optimized for 40 epochs and early stopping is used to avoid over-fitting. After each convolutional layer, a batch normalization layer is used. The batch size is chosen as 16. The training process is performed on an NVIDIA RTX A5000 GPU and the results are delivered on average after 3–4 hr of training.
During validation, the loss versus iterations is monitored and the model with the lowest validation error is selected. During inference/test time, the input is formed by the monthly temperature data coming from CMIP6 temperature maps that are stacked and given to the model in a feedforward evaluation. In each evaluation experiment, the target is defined as the month after the latest month in the input. After training with CMIP6 data, the selected model is further fine-tuned with ERA5 t2m data in order to increase the capability of the model in real-world forecasting scenarios. The fine-tuning process is carried out by following the same process as in the training. Monthly temperature data taken from ERA5 and the one-channel elevation map are stacked as a multichannel input and given to the network. During the fine-tuning stage, layers of the network are trained with the same learning rate and a weight decay of
![]() $ 1e-5 $
for 10 epochs with early stopping.
$ 1e-5 $
for 10 epochs with early stopping.
As an evaluation metric, the mean absolute error (MAE) (2) is chosen, where each
![]() $ {x}_{ij} $
and
$ {x}_{ij} $
and
![]() $ {y}_{ij} $
correspond to the predicted temperature and the ground truth temperature value of the corresponding grid, respectively. D refers to the number of longitudes, and M refers to the number of latitudes in the 2D spatial grid. All MAEs are summed and averaged across the temperature map to measure the overall error:
$ {y}_{ij} $
correspond to the predicted temperature and the ground truth temperature value of the corresponding grid, respectively. D refers to the number of longitudes, and M refers to the number of latitudes in the 2D spatial grid. All MAEs are summed and averaged across the temperature map to measure the overall error:
 $$ MAE=\frac{1}{D}\sum \limits_{j=1}^D\frac{1}{M}\sum \limits_{i=1}^M\mid {x}_{ij}-{y}_{ij}\mid . $$
$$ MAE=\frac{1}{D}\sum \limits_{j=1}^D\frac{1}{M}\sum \limits_{i=1}^M\mid {x}_{ij}-{y}_{ij}\mid . $$
3. Results and Discussion
Average MAE results over the validation dataset for temporal cases are provided in Table 1. As seen in this table, MAE ranges between 0.955 and 1.162. For comparison purposes, the MAE of the persistence forecast test (over the ERA5 validation dataset by copying the previous month’s temperature value as the target month’s prediction) is estimated as 2.62. This indicates that all models have improved the MAE significantly with respect to the persistence forecast baseline. It should be noted that out of six models, for each temporal case, 50% (or seven cases) of the lowest MAEs occur for Model 6 (M6). Three of the minimum MAEs occur for M5, and another three cases occur for M4, whereas only one minimum MAE occurs for M2. It is clear that ERA5 fine-tune has improved the performance significantly and using UNet++ with elevation is the best available model. Therefore, Model 6 was selected for the rest of the analysis. In order to choose the best temporal case for Model 6, we estimate the MAEs and rank them for four main continents (i.e., Africa, North America, Europe, and Asia) as well as their distribution among different seasons (i.e., Winter, Spring, Summer, and Fall). These values along with overall (as estimated over continents and seasons) are given in Figure 2. As seen in this figure, sequential cases (such as month 6, month 12, and even month 36) have higher ranks (hence lower performances) as compared to nonsequential cases. This is possibly due to the fact that the latter is able to recognize the strong seasonality in the data while sequential cases lack this ability. Among the nonsequential cases “Year 3 Month 2” case has the best performance as it has the best MAE rank for Fall, Spring, and Summer (and fourth for Winter). This case is the best for Africa and Asia continents, second for Europe, and third for North America. The overall rank for this case is estimated to be number one as well. Therefore, “Year 3 Month 2” is selected as the temporal case for Model 6 (CMIP6 with ERA5 fine-tune with UNet++ with elevation) for the rest of the analysis.
Table 1. Mean Absolute Error (MAE) values as estimated for the entire domain (lat:192 × lon:288) for each simulation conducted: 6 models × 14 cases = 84 simulations

Note: M1 and M4 are UNet; M2 and M5 are UNet with elevation; M3 and M6 are UNet++ with elevation.

Figure 2. MAE ranks of Model 6 for 14 temporal cases over four continents and four seasons.
For the selected temporal case we have conducted additional experiments where additional meteorological parameters were used. The results of the new experiments are given below in Table 2. This table indicates the MAE values as estimated for the entire domain (lat:192 × lon:288). According to the results presented in the table, “elevation + temperature” simulation has the minimum MAE among the examined variables. It should be noted that we have conducted simulations where we add meteorological parameters paired with temperature one by one and another simulation where all parameters were included. Although all parameter simulation with ERA5 fine-tune has the lowest MAE (0.991), it is still higher than the original model where elevation + temperature is used (0.975 with ERA5 fine-tune).
Table 2. Mean Absolute Error (MAE) values as estimated for the entire domain (lat:192 × lon: 288)

Note: Both M1 and M2 are UNet++. M1 is baseline, M2 is fine-tuned with ERA5. For this comparison, 7 ensembles instead of 9 used for training since vas and uas variables are not included in 2 ensembles of CMIP6.
The selected model settings were used in other deep-learning architectures (ResNet, PSPNet, and DeepLabV3) to investigate their performance. The results are provided in Table 3. As seen in this table, UNet++ with an MAE of 0.975 has the best performance while other models’ MAE values range between 1.025 and 1.738. According to these results, the UNet++ was selected to be used in this study.
Table 3. Mean absolute error (MAE) values as estimated for the entire domain (lat:192 × lon:288)

Note: Both M1 and M2 are UNet++. M1 is baseline, M2 is fine-tuned with ERA5. All experiments are done with elevation and temperature.
We compared the performance of the selected artificial intelligence (AI) model to the ensemble mean of the CMIP6 models. Figure 3 shows the MAE for the AI model and the mean of the CMIP6 ensemble as a function of time for the selected continents during the study period from 2016 to 2022. In Africa, both the AI and the CMIP6 model means have a similar error level (i.e., 0.27 versus 0.34) (Figure 3a). This is probably due to the fact that the climate in Africa is fairly uniform as a function of latitude and both models capture the overall climatology well. The AI model performs better compared to the mean CMIP6 in Asia and Europe. Although the inter-annual variability in the error between two different models overlaps, AI has significantly lower bias values. We believe that since the AI model has been trained by the CMIP6 ensemble, the model might inherit similar inter-annual variability. AI model’s MAE value for February 2020 for Europe, Asia, and North America is significantly lower as compared to the CMIP6 model (a difference of 3.2° for Europe, almost 1° for Asia, and 0.5° for North America), while they estimate closer values for Africa. The error in North America is the only place where the CMIP6 ensemble (
![]() $ 0.7 $
) is slightly better than the AI model (
$ 0.7 $
) is slightly better than the AI model (
![]() $ 0.71 $
) that needs further investigation. In both models, the error increases in the winter months, indicating that the models do not accurately represent the cold climate in the northern hemisphere.
$ 0.71 $
) that needs further investigation. In both models, the error increases in the winter months, indicating that the models do not accurately represent the cold climate in the northern hemisphere.

Figure 3. MAE results of AI and CMIP6 models for four different continents (a) Africa (b) Asia (c) Europe and (d) North America as estimated over the validation dataset.
The spatial distributions of the MAE fields for summer and winter for the AI and mean CMIP6 models are shown in Figure 4. Summer-time MAE in the AI model is fairly uniform and approximately 1.5°C over the continents (Figure 4a1). In contrast, the mean CMIP6 shows a relatively larger error (up to 5°C) in high-topography regions such as the Himalayas in Asia, the Andes in South America, the Rockies in North America, and the Alps in Europe (Figure 4a2). The MAE pattern in winter of the AI model is similar to the mean CMIP6 in high latitudes in the northern hemisphere (Figure 4b1,b2). This indicates that large-scale Jetstream bias from the CMIP6 models is responsible for the AI’s poor performance over Siberia and northern America. Once again, the error in winter is larger than in summer in both models, as we have shown in Figure 3. The performance of the AI model in terms of MAE is significantly better than that of the mean CMIP6 in both summer and winter.

Figure 4. (a) MAE fields of AI model in Summer (a1); CMIP6 model in Summer (a2); AI model in Winter (b1); and CMIP6 model in Winter (b2) for the validation dataset.
Next, at every grid point of the global domain (lat: 192, lon: 288), we calculated the temperature anomalies for each month to remove the mean of the month of that grid point. Then, we computed the scatter plot of absolute errors (AEs) of the mean CMIP6 and AI models for all grids as a function of these temperature anomalies (Figure 5a). The AI model performs better when the temperature anomalies are between
![]() $ -{5}^{\circ } $
C and
$ -{5}^{\circ } $
C and
![]() $ {5}^{\circ } $
C indicating that if a particular month is around the monthly mean, then the AI model predicts significantly better than the CMIP6 mean. However, if the month is part of an extreme event such as very cold (
$ {5}^{\circ } $
C indicating that if a particular month is around the monthly mean, then the AI model predicts significantly better than the CMIP6 mean. However, if the month is part of an extreme event such as very cold (
![]() $ \Delta T\approx -{10}^{\circ } $
C) or very hot (
$ \Delta T\approx -{10}^{\circ } $
C) or very hot (
![]() $ \Delta T\approx {10}^{\circ } $
C), AI’s performance is getting closer to the CMIP6 mean. To better understand the performance of the selected model, the box plots of the calculated AE based on temperature anomalies are given in Figure 5b. In all AI versus CMIP6 error bars for each temperature bin, AI model has significantly lower error values (for the median values and 25th and 75th percentiles). This outcome is even more pronounced, especially for the bins between −2 and + 2 (as shown on the x-axis).
$ \Delta T\approx {10}^{\circ } $
C), AI’s performance is getting closer to the CMIP6 mean. To better understand the performance of the selected model, the box plots of the calculated AE based on temperature anomalies are given in Figure 5b. In all AI versus CMIP6 error bars for each temperature bin, AI model has significantly lower error values (for the median values and 25th and 75th percentiles). This outcome is even more pronounced, especially for the bins between −2 and + 2 (as shown on the x-axis).

Figure 5. Absolute error plots of CMIP6 and AI model results for the validation dataset: (a) Scatter (b) Box plots.
In addition to scatter plot and box plots of AE values, other statistical values such as
![]() $ {R}^2 $
are used for understanding the relationship between observed and predicted temperature for all continents based on the results of the selected scenario. The results indicate that predicted values are well-fitting with the observed values in all continents. The
$ {R}^2 $
are used for understanding the relationship between observed and predicted temperature for all continents based on the results of the selected scenario. The results indicate that predicted values are well-fitting with the observed values in all continents. The
![]() $ {R}^2 $
values of all continents are close to 1, which imply the power of the AI model in seasonally predicting temperature around the world (see Supplementary Material S1).
$ {R}^2 $
values of all continents are close to 1, which imply the power of the AI model in seasonally predicting temperature around the world (see Supplementary Material S1).
4. Conclusion
We employed an advanced encoder–decoder model (UNet++) trained by state-of-the-art global CMIP6 ESM to forecast global temperatures a month ahead using the ERA5 reanalysis dataset. This study is a proof of concept for the use of this model in a complex climate system. We found that the deep-learning model predicts significantly better than the mean CMIP6 ensemble between 2016 and 2021. The AI model predicts the summer months more accurately than the winter months, similar to the mean CMIP6. Comparison of the results to other algorithms such as ResNet, PSPNet, and DeepLabv3 revealed that UNet++ provided the lowest MAE. Developed model is also used with additional meteorological parameters (u10, v10, zg500, psl, and pr) alongside 2 m temperature and elevation. The findings are striking since the simplest model (2 m temperature + elevation) provided the best result. In the future, we plan to improve our forecast time to seasonal predictions, that is, 3 months ahead.
Author contribution
Conceptualization: A.U., G.U., M.I.; Data curation: I.S., B.Y.; Data visualization: B.A., I.S., Y.A., A.U.; Methodology: A.U., G.U., M.I.; Software: B.A., I.S., B.Y., A.U.; Writing—original draft: B.A., Y.A.; Writing—review and editing: A.U., M.I., G.U. All authors approved the final submitted draft.
Competing interest
The authors declare none.
Data availability statement
Replication data and code can be found in Github: https://www.github.com/ituvisionlab/climate-ai.
Funding statement
This work received no specific grant from any funding agency, commercial or not-for-profit sectors.
Provenance statement
This article is part of the Climate Informatics 2023 proceedings and was accepted in Environmental Data Science on the basis of the Climate Informatics peer review process.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/eds.2023.24.