Fair equality of chances for prediction-based decisions

Abstract

This article presents a fairness principle for evaluating decision-making based on predictions: a decision rule is unfair when the individuals directly impacted by the decisions who are equal with respect to the features that justify inequalities in outcomes do not have the same statistical prospects of being benefited or harmed by them, irrespective of their socially salient morally arbitrary traits. The principle can be used to evaluate prediction-based decision-making from the point of view of a wide range of antecedently specified substantive views about justice in outcome distributions.

1. Introduction

In his biography of Thelonious Monk, the celebrated historian Robin D.G. Kelley told of a dream he once had that has become stock and trade in the conversations of jazz musicians. Apparently, Kelley, whose stepfather was a professional sax player and who played bass and piano as a young man, spent months trying to imitate Monk’s sound, which was famous for its up-tempo and dissonant style. Then, one day, Monk appeared to Kelley in the infamous dream and uttered the words every professional jazz player has heard at least once in their lifetime: ‘you are making the wrong mistakes’ (Kelley 2010).

Similar to jazz in Monk’s view, fairness is sometimes concerned with avoiding the ‘wrong’ mistakes, not with avoiding mistakes altogether. This is especially true of decisions based on statistical predictions. This idea of avoiding the wrong mistakes requires building a new type of theory, which involves two layers. In the first layer, wrong mistakes are characterized as mistakes, that is, as morally unjust outcomes. In the second, they are characterized as unfair mistakes, that is, morally unjust outcomes of procedures that have the tendency to affect socially salient groups in unequal ways. We have two goals in this article: first, to present a principle that can identify those mistakes that are unfair toward groups, and second, to show that this principle can guide the choice of some statistical fairness constraints, discussed mainly in the computer science community, in a way that is sensitive to some specific moral features of the decision context.

The principle we present is fair equality of chances, or FEC. The principle characterizes – in a formal and general way – how different (just or unjust) decisions must impact groups defined by socially salient characteristics in order for a decision rule to be unfair. In a nutshell, the principle requires that no inequality between groups emerges after conditioning on the feature, or set of features, that provides a valid moral justification of outcome inequality in the morally relevant outcomes produced by the procedure.

FEC applies to procedures, such as predictive procedures, that are not pure. Pure procedures do not rely on any prior definition of just outcomes (Rawls 1999). For example, a fair electoral procedure does not presuppose that justice will be achieved by electing a Democratic or Republican president. By contrast, the procedures to which FEC applies are used to make imperfect decisions as a means to achieve a just or justifiable distribution, where a definition of a just (or justified) distribution is given in advance. On one possible view, procedures that are a means to (independently defined) just outcome distributions are maximally just when they maximize the proportion of justly distributed outcomes. However, we argue that a procedure can be maximally just, in the sense just described and, at the same time, unfair toward groups. FEC specifies the conditions that must obtain in order for a procedure to count as fair toward different socially salient groups. These conditions cannot be defined by appealing to a single statistical criterion, for example, that the proportion or probability of errors must be the same for all groups, as we shall show. To identify a valid statistical criterion, a moral criterion has to be invoked.

The article is structured as follows. In section 2, we illustrate the tension between different statistical fairness criteria with an example. In section 3, we sharpen the conflict by providing some mathematical notation and a corresponding nomenclature. In section 4, we introduce the basic concepts of a new theory that provides a criterion for determining if a statistical fairness criterion is required by fairness. In section 5, we formulate the FEC principle. In section 6, we briefly present one intuitive argument for its justification – the other argument is produced by the coherence of the overall scheme. Section 7 shows that two of the most widely discussed statistical fairness criteria, that is, separation and sufficiency, correspond to mutually incompatible interpretations of the principle of FEC. This is a mathematical proof formulated in ordinary English – the formal argument is presented in the Appendix. In section 8, we apply this interpretation to two examples. There is a brief concluding section.

2. The Problem

Let us start with a concrete example. We draw this example from Long (2021), with minimal variation. Assume that 606 students have submitted exam papers to a course. Of these, 303 are from Buddhist students and 303 from Muslim ones. There are only two grades in the course, A and B, and we suppose that final papers could have the property of being a ‘true’ A paper or a ‘true’ B paper – the property of objectively deserving an A or a B. We shall call this property the ‘true label’, indicated with Y.

You follow the recommendations of an algorithm that, just like a real teacher, is a moderately fallible grader. We shall call the grade you give the ‘predicted label’, indicated with $\hat Y$ (Table 1). We assume, for argument’s sake, that 300 Buddhist students are graded with a B, but only three Muslim students receive this grade; the group of individuals who obtained an A consists of 300 Muslims and only three Buddhists. Your accuracy as a grader is described in Tables 2 and 3. We suppose that this accuracy is measured through a hypothetically independent test that is perfectly accurate in determining the true grade of each paper.

Table 1. Confusion table and predictive accuracy

Note: Generally speaking, we use a confusion table to represent the performance and fairness of a predictor for the general population. In binary classification, separation (the condition that the prediction is independent of group membership conditioned on the true label) is equivalent to the equality of false-positive and false-negative rates (i.e. b/(b+d) and c/(c+a), respectively) across groups. This quantity is also referred to as an equality of odds (Hardt et al. 2016). Sufficiency (the condition that the true label is independent of the group membership conditioned on the prediction) is equivalent to the equality of positive and negative predictive values (i.e. a/(a+b) and d/(c+d), respectively) across groups; it can be thought of as a special form of calibration.

Table 2. Confusion table of the grader’s performance in the Buddhist population

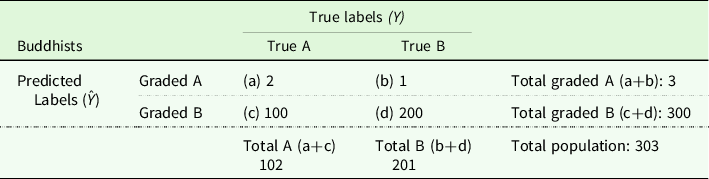
Table 3. Confusion table of the grader’s performance in the Muslim population

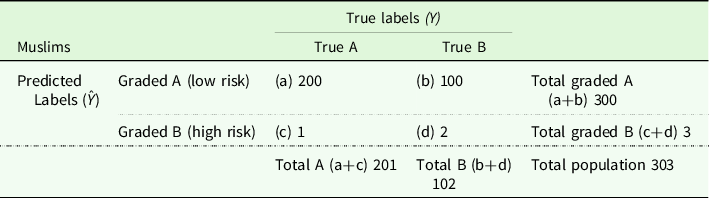
Let us assess the performance of the same predictor on the two different groups. We start by reading the table column-wise. The true positive rate, a/(a+c), is 2/102 (approx. 0.02) for Buddhists, meaning that out of 102 students with true A papers, only two of this population are classified correctly; this is the population of Buddhist true positive papers. The proportion of correctly judged A papers, the Muslim true positive papers, is much higher in the Muslim population. In the group of Buddhist true negatives, that is, Buddhist students actually delivering true B papers, the sensitivity of the predictor is much higher: out of 201 Buddhists with true B papers, 200 are correctly classified as such (200/201, approx. 0.99). Conversely, the Muslim true negative rate is much lower – that is, more B papers are erroneously marked with an A; the fact that there is also a difference in the false positive (b/(b+d)) and false negative (c/(c+a)) rates follows from the fact that these are equal to (1−true negative rate) and (1−true positive rate), respectively.

Notice that this apparently unbalanced performance of the predictor is compatible with the predictive value of the predictor being identical for both groups. This can be shown by reading the table row-wise. The likelihood of a true positive, given a positive prediction (a/(a+b)), is ⅔ for Buddhists. The likelihood of a true negative, given a negative prediction (d/(c+d)), is also ⅔. These are the same proportions in the Muslim population; obviously, the predictor is a significant improvement on an uninformed guess.

The result is that, in spite of your grades having the same probability of being correct independently of the religion of the student, Muslim students submitting B papers are much more likely to receive an A (on average) than Buddhist students and this distinction is the same in respect of A papers. This may be seen as Muslims having an advantage over Buddhists, even though the negative and positive predictive values are the same – that is, you are equally likely to be correct when you classify a paper as a B paper and when you classify a paper as an A paper, irrespective of the religion of the student.

The example above illustrates the dilemmatic choice that must be made when one assesses the fairness of a decision rule based on statistical predictions. On the one hand, the predictor is equally accurate for both groups and for both types of errors (false positives and false negatives). On the other hand, the errors for the two groups, conditional on the true labels, are unequally distributed. Both considerations are prima facie relevant to adjudicating the fairness of a decision based on this prediction. ¹ Thus, violating either seems to provide grounds for those who wish to criticize the predictor as unfair.

3. Sharpening the Conflict

Prediction-based decision-making is a two-step process (making a prediction based on some features, and then taking a decision based on the prediction). But for simplicity, we assume a direct link between positive/negative decisions, D, and the positive/negative predictions leading to those.

There are a few denominations in mathematics for the two fairness criteria at stake. Here, we shall refer to them as sufficiency and separation. Sufficiency and separation are often defined in terms of the conditional probabilities of correct and incorrect predictions relative to the true label. We choose the formulation in terms of the relation between outcomes and decisions (Barocas and Selbst 2016) because we assume here that what can be fair and unfair is a decision, not a prediction in itself. We can thus simplify the discussion somewhat by stipulating that a prediction of A-paper ( $\hat Y$ =1) corresponds to a decision to provide the grade A (D=1), and vice versa (that is, $\hat Y$ =0 implies and is implied by D=0).

Sufficiency can be expressed, then, as the requirement that the group one belongs to, A, should not influence the likelihood of a true label, Y, for any individual about whom the same decision, D, is made. In our final formulation:

Sufficiency: Individuals about whom the same decision D is made have the same expectations of the true label, Y, that is, the same statistical prospects of being a true positive, regardless of their group membership, and the same statistical prospects of being a true negative, regardless of their group membership.

This is the statistical condition that the decision rule in the example in the previous section initially satisfies. The probability that a paper will be correctly graded B is the same irrespective of the group to which it belongs. The probability that a paper will be correctly graded A is also the same irrespective of the group to which it belongs.

The statistical condition of separation, on the other hand, represents the idea that individuals with the same true label (e.g. those who, according to the objective features of the paper, merit an A) are equally likely to receive the same decision (e.g. receive an A grade). In other words, one splits the population into different categories that correspond to the true labels (e.g. A papers, B papers), and then one requires that group membership (e.g. religion) is irrelevant to the statistical prospects of either decision:

Separation: Individuals with the same true label Y have the same expectations of positive or negative decision D; that is, true positives have the same statistical prospects of a positive decision, and true negatives have the same statistical prospects of a negative decision, regardless of their group membership.

If separation is met, the probability that a paper deserving an A receives an A is the same irrespective of the group to which it belongs, and the probability that a paper deserving a B receives a B is the same irrespective of the group to which it belongs.

As pointed out in the previous section, it is logically impossible for a decision process to meet both these conditions unless the decision process is perfectly accurate or the distribution of the trait of interest is equal across subgroups. That is, sufficiency and separation can both be met only if (i) the predictor with perfect accuracy identifies A and B papers or (ii) writing A papers and writing B papers is equally common among Buddhists and Muslims. In all other situations, a decision process can meet sufficiency or separation, but not both (Chouldechova 2017; Kleinberg et al. 2017; Berk et al. 2021; Fazelpour and Danks 2021).

In the following section, we introduce a principle that provides a link between the general conception of fairness we defend – FEC – and sufficiency and separation.

Our aim is to present a conception of fairness that – considering the below-stated limitations – can (contribute to) guide policymakers in the inevitable choice between sufficiency and separation. Assuming that our theory – FEC – defines what is fair in the domain of decision rules based on statistical predictions, we show that violating sufficiency is unfair if and only if a specific set of moral ² and prudential ³ conditions are satisfied, while violating separation is unfair if and only if another specific set of moral and prudential conditions are satisfied. When neither set of moral and prudential conditions are satisfied, neither sufficiency nor separation can be considered to be equivalent (i.e. reducible) to the fairness principle we identify. ⁴

Even if it turns out that FEC rarely justifies using sufficiency or separation as criteria of fairness, we do not regard this as a weakness of our theory. FEC may most often imply that satisfying neither sufficiency nor separation is relevant for fairness. That negative conclusion is also a valuable moral insight that can be derived from it. It may be entirely coherent with the critique of small-scale ideal theorizing (Lipton and Fazelpour 2020) and it may further support the view that current statistical criteria are not applicable (Lipton and Fazelpour 2020).

4. Building up to Fair Equality of Chances

To achieve some terminological clarity, in what follows, we shall use the expression ‘fair’ to describe an intuitively morally desirable feature of procedures (yet to be characterized) and ‘just’ to describe outcomes that are desirable from the viewpoint of justice, when justice is defined independently of any procedural consideration. Our theory takes justice to be a distribution according to desert*, where we take desert* to be anything that justifies outcome inequality (in a procedure-independent sense). Desert* could refer to needs (Wiggins 1987; Herlitz and Horan 2016), responsibility (Arneson 1989; Roemer 1993), or, indeed, desert (Feldman 2016; Brouwer and Mulligan 2019), depending on what your favourite view of justice happens to be. FEC is, in fact, compatible with the justification of inequalities being context-dependent (Miller 1999). ⁵

Thus, the first element of our framework is:

1. Justifier. The value of J measures the degree to which the individual deserves* the good (advantage or disadvantage, measured as U) a procedure allocates to them. ⁶

The value of J is a function of the properties that make that individual deserving* (desert* properties), such as the individual’s needs, responsibility, and contribution, which are answers to substantive moral questions delivered by theories other than FEC. ⁷

Mathematically speaking, we use J to indicate potentially multidimensional, continuous random variables. For simplicity, we will restrict attention to one-dimensional, ordinal J, for example, a person’s contribution or need, as defined by a single ordinal value (e.g. any two individuals are either equally deserving, or one is more deserving than the other). When the random variable J takes the same values for two or more individuals, the individuals in question are described as being equally deserving*.

The introduction of the concept of desert*, although abstract and unsubstantiated, is necessary because FEC must operate at a different level of abstraction from most theories of justice. FEC aims to characterize a dimension of the unfairness of imperfect procedures. Imperfect procedures, by definition, aim to realize a just distribution, where justice is defined for outcomes in advance of the procedure itself (Rawls 1999). By specifying FEC in terms of desert* (as opposed to effort, substantive desert, or need, etc.), we are able to characterize, at an abstract level, the relation between outcome justice and procedural fairness in a way that is independent of specific (and contentious) premises about outcome justice.

If ‘unfair’ simply means ‘produces undeserved* inequalities’ (or equivalently, ‘unjust outcomes’), every procedure that is imperfect is necessarily unfair. Ideally, outcome inequalities should track desert* inequalities perfectly. ⁸ Yet, by definition, only a perfect procedure allocates advantages and disadvantages according to what each individual deserves*. Imperfect procedures will sometimes permit that individuals, equal in desert*, will receive unequal outcomes. For example, while the majority of guilty individuals are convicted, and the majority of innocent individuals are acquitted, some guilty individuals are acquitted, and some innocent individuals are convicted. These individuals do not have exactly the same features; for example, they may be born on different days or be judged at different moments in time. So, there will typically always be individuals (in the case of imperfect procedures) who are equal in their desert* (e.g. they are both innocent), who differ in non-desert* traits (e.g. the moment at which they are judged), and who receive different outcomes (Di Bello and O’Neil 2020).

This is a problem because a principle of fairness for imperfect procedures should be able to say that a decision procedure that is more advantageous for White people than for Black people in the United States is unfair. And if it is to be applicable to imperfect procedures, it must also be able to say that a decision procedure that disproportionately benefits people born on uneven dates (e.g. 1st, 3rd and 5th of every month) may not be, for that reason, unfair. For example, on a need-based theory of justice, anything that is not need is not desert*. Relative to need, the fact that one is born on an odd day is as morally arbitrary as being a woman. In other words, given a theory of justice determining desert*, every feature that is not desert* is morally arbitrary and, as a matter of principle, equally so.

We introduce the concept of a morally arbitrary* property, that is, morally arbitrary with a * sign, to signify a feature that is not desert*, and that, in addition, identifies a socially salient group:

a group is socially salient if perceived membership of it is important to the structure of social interactions across a wide range of social contexts. (Lippert-Rasmussen 2007)

We, therefore, define a second variable, G, that takes the value of the morally arbitrary* property of an individual that corresponds to the socially salient group to which that individual belongs. When a combination of independent, morally arbitrary* properties (e.g. gender and race) is distinctively socially salient, then the relevant intersectional groups (e.g. White male) could be considered instead. ⁹

2. Group. The random value G indicates a property (or combination of properties) of the individual that is not desert* and that is socially salient in the society affected by the procedure under evaluation.

Again, we use G to indicate potentially multidimensional, continuous random variables. Note that categorical variables are subsumed by continuous variables, so this does not restrict the definition of G in any way. For simplicity, we will restrict attention to categorical values, for example, female or male, Black or White, and so on. When the random variable G takes the same values for two or more individuals, the individuals in question are described as belonging to the same morally arbitrary* group.

Notice further that the definition of desert* explicitly mentions U, which is the chosen metric for measuring advantageous and disadvantageous outcomes. When Definitions 2 and 3 refer to inequalities, what is intended thereby is also an inequality in the distribution of U. This gives us the third and last element in the framework:

Utility* indicated with U. The value of U measures the advantage or disadvantage of individuals resulting from the allocation of goods by the procedure in question. ¹⁰

We use utility* as shorthand for outcomes that are in any way beneficial or harmful, advantageous or disadvantageous for individuals. In the example of the grader, receiving an A could amount to one unit of utility for the individual, while receiving a B could amount to 0.5, ¹¹ capturing the belief that the benefit of every individual from receiving an A is twice that of the benefit from receiving a B. The star in utility* indicates that utility* is not ‘utility’ in the strict sense of well-being or what is good for a person. Utility* can also be regarded as a social primary good (Rawls 1999) or capability (Sen 1995), following Roemer (1993).

This agnosticism is not a means to broaden the applicability of FEC in practice. It is a principled demand for a theory of imperfect procedural justice. The nature of U is implied by how just outcomes are defined, in the theory characterizing the goal of the procedure as just. ¹²

Morally arbitrary* properties have been defined as those properties that are not desert* and that are socially salient. Clearly, it is logically possible that a property that is not desert* is not socially salient. For example, the fact that one is born on an odd or even day does not usually justify treating people unequally. But it is also not socially salient. If a procedure is imperfect, it is possible that some inequalities emerge, by virtue of its application, among people who are equal in their deserts* but different in those traits. For example, innocent people born on an odd date are more often acquitted than those born on an even date. We shall refer to these traits as luck*. Or equivalently:

3. Luck*, anything other than G that impacts U but cannot be explained by J.

We believe that the following view of fairness is intuitively plausible. Every inequality in utility* between people who are equally deserving* is unjust. But procedures generating such inequalities are not necessarily unfair. If equally deserving members of groups, irrelevant from the point of view of social salience, have unequal expectations of utility*, an imperfect procedure may still be fair even if it is only imperfectly just. That is to say, an imperfect procedure can distribute benefits unequally between equally deserving* individuals who differ in luck* and still be fair.

The intuition modelled by FEC is that, in order to be fair, luck* has to be neutral relative to the groups that are socially salient, that is, morally arbitrary*. A procedure generating inequality due to luck* ought not to have a disposition to favour one morally arbitrary* group over any other (in the context in which it operates), where the relevant inequalities are within classes defined by equality of desert*. Yet, it is possible for some individuals to be lucky* and receive better treatment from the procedure than other equally deserving individuals. For example, it may turn out that individuals born on even days are more likely to obtain some good that they deserve*, compared with equally deserving* individuals born on odd days. This may happen if being born on an even day correlates with some indicator that is used by the procedure to make accurate predictions and efficient decisions. This can be fair if, despite the imbalance across the two birthday classes, no morally arbitrary* (that is, socially salient) group is advantaged relative to any other.

A formal definition of luck* neutrality has been offered in an attempt to characterize the ‘Rawlsian’ idea of equality of opportunity mathematically (Lefranc et al. 2009). The label of luck* neutrality to denote this condition of statistical independence is indeed such a proposal:

Luck* neutrality: Luck* is neutral if and only if for individuals with the same desert* value, J, expectations of utility, U, do not statistically depend on their G.

The mathematical formulation of luck* neutrality assumes E to be the expectation value given a known probability distribution of utility* (U). Luck* is neutral if and only if ∀(g,g′) ∀ j, E(U|g,j)=E(U|g′,j). The expected value of U is allowed to covary with J. But, keeping J fixed (i.e. when J is at a given value j), utility is required not to covary with G. ¹³ This is what makes luck* neutral.

So far, we have presented the following building blocks for a theory of (imperfect) prediction-based decisions:

1. 1. Justifier (J). The value of J measures the degree to which the individual deserves* the advantage or disadvantage a procedure allocates to him or her.

2. 2. Group (G). The random value G indicates a property (or combination of properties) of the individual that is not desert* and that is socially salient in the society affected by the procedure under evaluation.

3. 3. Utility* (U). The value of U measures the advantage or disadvantage of individuals resulting from the allocation of goods by the procedure in question.

4. 4. Luck*. ¹⁴ Anything other than G that impacts U but cannot be explained by J.

The theory assumes that the desert* properties, morally arbitrary* group membership, and utility* distributed to individuals by a procedure can be described by possible values of the variables J, G and U. Even if one allows these variables to be multidimensional, continuous random variables, quantification itself may be thought to involve a radical simplification or gross approximation of the relevant moral facts. We suppose that there may be cases in which such approximation is plausible and justifiable; ¹⁵ to some extent, it is hardly avoidable if one is attempting to make sense of statistical fairness definitions expressed in mathematical language from the moral point of view.

5. Fair Equality of Chances

It is now possible to succinctly express our view of the fairness of imperfect procedures. We defend a view of imperfect procedural fairness which, loosely stated, claims that a procedure is unfair if it allocates advantages and disadvantages to the predictable advantage or disadvantage of certain groups, across classes of equally deserving* individuals. Let us clarify this definition.

First, we defend a principle that is a necessary but not sufficient condition of procedural fairness. Several philosophers have discussed procedural justice by invoking criteria whose justification is independent of the value attached to the goals the procedure is intended to achieve. ¹⁶ Our theory is agnostic with respect to the question of whether the procedural justice of imperfect procedures ought to be sensitive to any procedural consideration that can be expressed fully independently from an already given conception of distributive (outcome) justice. Since the existence of other necessary conditions of procedural fairness cannot be ruled out a priori, however, our account of fairness (FEC) will not be defended as a necessary and sufficient condition of procedural justice. Thus, we only claim that FEC represents a necessary condition for the fairness of imperfect procedures. That is:

T1 (necessary condition for procedural fairness): an imperfect procedure (including an imperfect prediction-based decision rule) is fair only if it satisfies the FEC principle.

T2 (definition of FEC): an imperfect procedure satisfies FEC if and only if luck* is neutral,

which can be rewritten as:

T2’: an imperfect procedure satisfies FEC if and only if ∀(g,g′) ∀ j, E(U|g,j)=E(U|g′,j)),

or equivalently:

T2”: an imperfect procedure satisfies FEC if and only if individuals equal in their values for J have the same expectations of having U, irrespective of their G values. ¹⁷

If one replaces the variables J, U and G, with the vocabulary introduced above, what we get is the informal statement of FEC:

T2’”: an imperfect procedure satisfies FEC if equally deserving* individuals have the same expectations of utility*, irrespective of their morally arbitrary* traits.

One implication of T2 is that, no matter its other virtues, an imperfect procedure that does not satisfy FEC counts as necessarily (procedurally) unfair. This provides us with an empirically testable condition of the fairness of a procedure given settled values for features in J, G and U (at least, for a particular context). In particular, when the relevant type of data exists for J, G and U, it may allow one to test a statistical procedure for its fairness. The fairness of prediction-based decisions does not require perfectly just outcomes: this is a plausible contention if justice ideally requires perfect predictions, since statistical methods are rarely, if ever, perfectly accurate.

One implication of this theory is that outcome justice and procedural fairness are related but distinct. The theory applies, in a way that we find plausible, to decision-making procedures other than those based on statistical predictions. For example, a random lottery is procedurally fair according to FEC no matter what counts as morally arbitrary*. Yet, FEC is compatible with claiming that lotteries typically promote injustice (individuals end up with advantages or disadvantages that are clearly undeserved*). Conversely, a procedure may minimize the amount of injustice and be unfair, in so far as it tends to produce undeserved* advantages for (members of) some morally arbitrary* groups in imbalanced proportions. A fair prediction-based decision rule may be feasible, at least when considering a limited number of morally arbitrary* groups. For example, if gender is the only morally arbitrary* property, a prediction-based decision is only required to generate no statistically significant inequalities between equally deserving* men and women. This procedure may generate a greater proportion of unjust outcomes than the most just (but unfair) feasible procedure, but a smaller proportion of unjust outcomes than a purely random one.

Let us now deal with two distinct objections that can be raised against our account. Our definition of FEC, as shown, builds on Lefranc et al.’s (2009) idea of ‘neutral luck’, something which neither justifies inequality morally nor has to be corrected for the outcome to be fully just. ¹⁸

The idea of the fair distribution of chances is of course not new in ethics and political philosophy. But the widely discussed approach of John Broome (1984), for example, implies a far stronger requirement, than either sufficiency or separation. Broome conceives fairness to require equal chances of X among those individuals who have equally strong claims to X, when it is impossible to distribute X equally. Thus, Broome’s idea is satisfied by lotteries, which give every individual who participates in them, exactly the same chances, at the individual level. According to Sune Holm (2023) sufficiency and separation can be justified when they realize Broomean conditions of fairness.

If Holm’s view is correct, however, there is little hope that fairness consists in either. Broomean fairness is far stronger than equality in the true positive or false positive rate, for example (Castro and Loi 2023). In the example provided at the beginning of this article, Broomean fair chances require that all individuals with a ‘true A’ paper have, individually, the same chances of ending up with an A. But this is not guaranteed by equality in the false positive rate or even by equality in the false positive and in the false negative rate. These are compatible with individuals having very different chances of receiving an A, provided that these inequalities compensate each other at the group level (Castro and Loi 2023).

The Broomean account is very unlikely to bridge the gap between the statistical measures of group fairness in use and our intuitions about what is just or fair. After all, most algorithmic decisions are not randomized but deterministic, given individual (input) features (Castro and Loi 2023). So, our non-Broomean approach, which relies on a different conceptualization of fair chances, ¹⁹ provides an interesting alternative.

Second, it may be objected that FEC is too strong to count as a necessary condition for imperfect procedural fairness. Consider the case discussed in section 1, in which the unequal false positive rate is due to the proportion of true A papers among young Buddhist students being lower than the proportion of true A papers among young Muslim students. In our account, this is not an instance of neutral luck, even if the unequal (average) prospects of the two types of students are not caused by their religious-group memberships. For example, suppose that the grader is less able to adequately rate the papers of young students compared with older students, and the age distribution of the two religious groups differs. This leads to a difference in the proportion of objectively good ‘A’ papers that are classified as ‘B’ papers (Beigang 2023). The non-neutrality of the grader (given the distribution of age in the different religious groups) is morally significant, provided that the correlation between age and the socially salient trait ‘religion’ is a robust, structural fact about the society in which the grader lives. ²⁰ As the groups are morally arbitrary*, and therefore socially salient, this non-neutrality may produce inequalities between the two groups that are reasons for moral concern, as we discuss next.

6. The Intuitive Justification of FEC

It is important to stress that FEC requires equal expectations of utility among equally deserving* individuals who belong to different morally arbitrary* groups, where groups that are morally arbitrary* are also socially salient by definition. The justification of FEC is that when groups are socially salient, group inequality matters, at least pro tanto. It is not the purpose of this article to provide a foundational argument for the view that group inequality matters as such, from the moral point of view. The justification we offer here is rather minimalist, and it involves two different modes of justification:

1. (a) an appeal to intuitions;

2. (b) coherence in wide reflective equilibrium (Rawls 1999: 199) between this view and plausible intuitions about the cases of prediction-based decisions discussed in sections 7 and 8.

Here we provide the intuitive argument; the reflective equilibrium argument is delivered by the article as a whole. The intuitive argument is as follows. Suppose that we have two groups that are socially salient, for example, in the US, White people and Black people. It turns out that there is an avoidable unjustified inequality in the distribution of some goods between the two. Notice that we are not implying that the distribution is due to race. Simply, there is an inequality between the two races, as groups, that, by hypothesis, is not justified. For example, the rate at which innocent Black men are convicted is 30 per cent, while the rate at which innocent White men are convicted is 20 per cent. We maintain that, intuitively, this inequality is unfair, at least pro tanto. The same intuition of pro tanto unfairness concerns other cases. For example, suppose that 80 per cent of the male children in need receive welfare assistance, but only 70 per cent of female needy children receive welfare assistance. We maintain that such intuitions persist even when we are told that race or gender are not the causes of the inequality but something else is (something else that is non-ephemerally correlated with gender and race). ²¹ Provided that the association is robust, the inequality is felt to be morally problematic, morally objectionable and unfair. This inequality is identified by determining the statistical prospects of an individual qua generic member of the reference class of the socially salient group to which that individual belongs, and comparing generic members of one group to members in a different group who are equal in J.

We believe that the intuition generalizes to all cases in which inequality between individuals equal in their desert* correlates with morally arbitrary* groups. We speculate that it is a distinguishing characteristic of socially salient groups that a procedure generating undeserved* inequalities between them feels, at least pro tanto, unfair. It is also felt to be more unfair than one generating the same amount of undeserved* inequalities but without any correlation with such groups.

7. Interpreting Statistical Fairness Constraints

In this section, we use FEC to interpret separation and sufficiency. We show that separation and sufficiency are special forms of our notion of fairness that correspond to a specific relation between the variables U (utility*), G (morally arbitrary* traits) and J (desert*). According to T2”:

Prediction-based decisions (an example of imperfect procedures) satisfy FEC if and only if individuals with the same J have the same expectations of having U, irrespective of their values for G.

Let us recall the informal definitions of sufficiency and separation and compare them with the above definition of FEC:

Sufficiency: Individuals about whom the same decision, D, is made have the same expectation of having the same true label, Y, that is, the same statistical prospects of being a true positive, regardless of their group membership, and the same statistical prospects of being a true negative, regardless of their group membership.

FEC can be turned into sufficiency by substituting ‘the same J’ with ‘about whom the same decision, D, is made’ and ‘U’ with ‘the same true label, Y’. ²² That is, prediction-based decisions that satisfy sufficiency, satisfy FEC if and only if:

1. (a) that which harms and benefits individuals is the future true outcome (or true label), Y,

2. (b) that which justifies inequality is the decision, D, and

3. (c) G is group membership in the sense that is meant in separation and sufficiency.

Let us now consider the following:

Separation: Individuals with the same true label, Y, have the same expectations of receiving the positive and negative decisions, D, that is, true positives have the same statistical prospects of a positive decision, and true negatives have the same statistical prospects of a negative decision, regardless of their group membership.

In order to obtain separation from FEC, one must simply substitute ‘J’ with ‘true label, Y’ and ‘having U’ with ‘receiving the positive and negative decisions, D’ ²³ . Thus, a prediction-based decision that satisfies separation satisfies FEC if and only if:

1. (a) that which harms and benefits individuals is the decision, D,

2. (b) that which justifies inequality is the future true outcome (or true label), Y, and

3. (c) G is group membership.

This result can be used as a guide to choose which fairness criterion, separation or sufficiency, is more appropriate in a given context.

However, it is possible that one variable can be both a harm and a benefit, or a benefit is regarded as a function of both the decision and group membership. Our theory entails that, when this is the case, FEC is satisfied by neither separation nor sufficiency. In other words, the cases in which separation or sufficiency are required by fairness are highly special ones, those in which decisions can be identified with predictions and either the decision or the true label capture the utility* or justifiers of a decision but not both.

Notice that sufficiency and separation refer to the (historically) true labels, indicated with Y. Thus, it is normally possible to determine if FEC was satisfied, retrospectively, by procedures that have already been used to make decisions and when salient outcomes of different decisions on heterogeneous types of individuals can be observed. Decision-makers typically cannot know the future outcomes of individuals about which they make decisions at the moment in which they have to make the decision. It is only possible to know if a procedure has been fair retrospectively, when observations of the actual values of Y become available. ²⁴

8. Applications

In this section, we discuss two cases in which the principle of FEC plausibly provides clear advice on whether separation or sufficiency is required in a statistical-prediction-based decision rule. In the first case, FEC implies separation because – we argue – it is plausible that J=Y and U=D. In the second case, FEC implies sufficiency because it is plausible that J=D and U=Y. Hopefully, the moral analysis of these cases illustrates the insights that can be gained from FEC.

Case 1: Distributing cash assistance to keep children in school

Suppose a city is developing a statistical model to allocate cash assistance designed to keep children in school. The true label, Y, specifies whether the child leaves school before completing secondary education.

First step: Identify the just outcomes. The first analytical step is to identify the just outcome distribution that the decision-based procedure intends to achieve. At least for the sake of argument, let us assume that an ideally just outcome distribution is the one giving cash assistance to all and only the children who otherwise leave school prematurely. This theory identifies two classes of unjust outcomes: (a) when a child who leaves school prematurely does not receive cash assistance; and (b) when a child who does not leave school prematurely receives cash assistance.

Second step: Identify the conceptions of utility* and desert* implied by the characterization of just outcomes. Assuming the validity of the above account of just outcomes, the benefit is cash assistance, which, for simplicity, we assume to be equal in every case and equally beneficial to every recipient. Given this simplification, it is correct that, when cash is provided U takes the value of 1 and 0 otherwise. In the theory of just outcomes, which is assumed to be valid, what justifies receiving cash assistance is, uniquely, being a child who leaves school prematurely. ²⁵ Thus, in this special case, J* = Y, the true label ‘the child has left school’ (assuming our observations of Y are not biased in favour of either group).

Third step: Identify the relevant groups. Finally, we assume for the sake of simplicity that the only socially salient difference between the two groups of children is their race. So G, in this case, is race, which is the same variable used in the statistical criteria of sufficiency and separation and in the FEC principle.

In these circumstances, FEC corresponds to separation. Separation involves two claims, one for positive and the other for negative cases. First, all children who have actually left school (Y=1) should have had the same probability of receiving cash assistance (D=1), irrespective of their race. Second, all children who do not need cash assistance (Y=0) should have the same expectation of receiving assistance (D=1) as a beneficial side-effect of being misclassified, irrespective of their race.

The counterintuitive side-effect of this choice could be the following: if Black children are more likely as a group to leave school prematurely than White children and separation is satisfied, the White children receiving the cash benefit will be less likely, on average as a group, to leave school prematurely; conversely, Black children who are not selected for cash assistance will be more likely to leave school prematurely, on average, than the White children who are not selected. This may seem to advantage White children over Black children, but, in fact, it is the result of achieving separation. This consequence makes the recommendation of our theory somewhat counterintuitive; however, since every violation of separation or sufficiency is, to some extent, counterintuitive, we believe that this is the best argument that can be provided for one of the two counterintuitive results being the morally appropriate one.

Case 2: Recommendations to take risks

A company (F1 company) promotes the opportunity of experiencing a Formula 1 race for amateur drivers. The client is permitted to race alone and to compete with others in a challenge to set the fastest racing time (as an F1 qualifier). For safety reasons, only drivers sufficiently likely to avoid fatal crashes are recommended to race. For this reason, they assess the risk of a fatal crash based on the data points collected after 10 hours of lone driving.

First step: Identify the just outcomes. In order to illustrate a case that supports sufficiency, we will select a somewhat unusual moral theory – hoping that the example retains at least some intuitive plausibility.

We suppose that those who have been recommended to avoid racing due to its high risk have no moral claim to avoid death by accident in the race, while all those who have been given the recommendation to race morally deserve to survive. This formulation is rough, but it may capture, with significant simplifications, the core intuition of Scanlon’s (1998: 257) view on the moral relevance of warnings. ²⁶

Let us now unpack the corresponding assumptions about utility* and desert*. First, we notice that the only benefit considered in this account of outcome justice is surviving the race. That is to say, we ignore the utility derived from the enjoyment of the race. Possibly, if our account of the just distribution had considered that element too, it would not have supported sufficiency but a different statistical criterion instead. Our choice of a theory of just outcomes is ad hoc, in the sense that it is meant to illustrate the logical possibility of selecting sufficiency as a fairness criterion. But, as argued next, it cannot be considered a weakness of FEC itself.

Second step: Identify the conceptions of utility* and desert* implied by the characterization of just outcomes. Let us suppose that it is justifiable to ignore damage suffered from a less-than-fatal crash. This assumption is implied by the moral theory of just outcomes we characterized at the outset, which was chosen for its simplicity. This theory of justice describes the possible outcomes in such a way that it is only possible to pair them with two utility* values: U=0 for a fatal crash and U=1 for every other outcome. Clearly, the theory is not sufficiently fine-grained to provide guidance in real life. For that reason, it is not fully plausible. We imposed this further simplification because we also aim to illustrate sufficiency as fulfilled by a binary classifier, thus keeping the formal element to a minimum. ²⁷

For simplicity’s sake, we assume that it is justifiable to simplify our observations about the observed outcomes. We assume Y=0 indicates the event of a fatal crash and Y=1 its avoidance. Again, these observations are, by assumption, not biased against any morally arbitrary* group. Thus, in this case, plausibly, U=Y.

Let us now turn to desert*. One must ask whether, according to this theory, all individuals have an equally strong claim to U, where the values of U correspond to the two possible outcomes of the race in our ultra-simplified account of the case. The theory of justice described at the outset denies this. It maintains that all individuals, and only those, receiving the recommendation to race equally deserve* to survive, and those who were told to abstain from the race do not deserve* to survive to a comparable degree; the strength of the moral claim of individuals to receive the good ‘survival’ after racing depends on the recommendation received before the race. Thus, this theory treats the recommendation received by the individual as the justifier of inequality. Since the recommendation an individual receives is the decision D (e.g. the outputs of the procedure are such warnings), this can be described as a case in which J=D.

If all these conditions are met, FEC requires that one considers sufficiency as the relevant standard for this case. That is to say, the tool should be considered fair if and only if clients who are recommended to race are equally likely to survive, irrespective of their socially salient group, and if clients who are allowed to race are equally likely to die, irrespective of their socially salient group. FEC implies that violating sufficiency is unfair.

This judgement seems sufficiently intuitive to us. To the extent that one focuses on a fair distribution of the risk of death, sufficiency is indeed an appropriate criterion for this case. This risk may be allowed to vary systematically between groups of individuals who have been given opposite recommendations. But, among those individuals, it should not vary systematically across the socially salient groups to which they belong.

Notice that the plausibility of FEC always needs to be determined relative to some theory of the just outcome distribution that is not implied by it. Evidently, the moral assertions FEC supports are only as good as the account of just outcomes one assumes to be valid.

Admittedly, it is hard to provide a persuasive illustration of a context in which sufficiency realizes FEC, given a fully morally plausible theory of outcome justice, in a few pages. We do not believe that all possible cases in which sufficiency is supported by FEC must rely on implausible theories of outcome justice. ²⁸ We also do not believe that, if that were the case, it would imply that FEC is fundamentally misguided; after all, we could live in a moral world in which sufficiency is not a valid criterion of fairness. It could be the case that no valid theory of just outcomes implies the validity of sufficiency in circumstances that actually obtain, or that could plausibly be taken to obtain. Even in this scenario, FEC retains its utility as a tool to determine what would have to be the case (morally speaking) for sufficiency to be morally relevant to imperfect procedural justice. However, we believe that the opposite is the case, and the exploration of contexts and moral theories supporting sufficiency seems to support this conjecture.

9. Conclusions

In this article, we have illustrated the complications that arise when one attempts to evaluate the fairness of different decision rules based on statistical predictions with everyday normative concepts and moral-philosophical theories. Both everyday language and moral-philosophical theories turn out to be vague at best when one turns to evaluations of predictive models, and this creates significant challenges since the alternative mathematical translations of the fairness criteria provide us with a genuine dilemma: several fairness criteria appear plausible, but it is impossible to satisfy them at the same time.

However, we have argued that this apparent impossibility theorem for decision rules based on predictions can, in some cases, be dissolved by a better understanding of: first, the relevant harms and benefits generated by the predictions; second, the factors that justify inequalities (referred to as “justifiers”, or “desert*”) and those that should not align with them (termed “arbitrary* traits”); and third, the unjust inequalities that are not unfair – namely, those relating to unjust outcomes in a statistically neutral way (defined as “luck*”).

We have argued that the FEC principle is supported in reflective equilibrium by its coherence with two statistical fairness criteria (separation and sufficiency) and with the intuition that inequality between groups matters morally when the groups are socially salient. ²⁹ FEC implies that an (imperfect) procedure resulting in unjustified inequalities robustly correlated with socially salient groups is not fair. By contrast, an imperfect procedure can be fair even if it generates inequalities correlated with socially salient groups when this inequality in statistical prospects disappears for groups consisting of individuals with the same desert* characteristics. ³⁰

Our hope is that this approach enables philosophers and stakeholders to articulate moral arguments in favour of or against sufficiency and separation as relevant fairness constraints when modelling statistical predictors through machine learning, at least in those contexts in which these statistical criteria are appropriate. Indeed, our demonstration reveals that as Fair Equality of Chances (FEC) establishes a necessary condition within instances of imperfect procedural justice, there are circumstances where fairness necessitates the adoption of separation or sufficiency principles.

To the best of our knowledge, FEC is the only framework that works out the implications of treating questions of predictive or statistical fairness as questions of imperfect procedural justice. This is a dimension of fairness irreducible to either outcome justice or pure procedural justice. Our theory does not provide an answer to the question, ‘is this decision-making procedure fair?’ alone. FEC must always be supplemented by an account of outcome justice. For clearly, imperfect procedural justice can only be defined relative to the (perfect) conception of outcome justice that the (imperfect) procedure is supposed to bring about. However, FEC is compatible with a large class of such theories. Our theory necessitates the introduction of new theoretical concepts, desert*, utility* and luck*. FEC characterizes procedural fairness as a mathematical relation between the ideally just outcome distribution and the one actually achieved by the procedure. The concepts with the * sign enable a purely formal description of the relation between procedural fairness and outcome justice while sidestepping all commitments to specific accounts of the latter.

Moreover, fairness might not be the only ethical desideratum of imperfect procedures. Achieving a socially optimal decision rule may require balancing efficiency and fair equality of chances, as these objectives may sometimes be in conflict with each other (Corbett-Davies et al. 2017). Moreover, we have assumed the egalitarian idea that fairness consists of some kind of equality. However, it is also worth exploring a maximin version of the first principle of a theory of imperfect procedural justice, which is satisfied when the greatest utility is produced for the group with the lowest utility among those with equal desert*. ³¹