1. Introduction
Many economic models assume that people are exclusively pursuing their material self-interest, as opposed to pursuing social goals. Experimental economists have been gathering evidence that people often violate this assumption of self-interest (Güth et al. Reference Güth, Schmittberger and Schwarze1982; Fehr et al. Reference Fehr, Kirchsteiger and Riedl1993; Berg et al. Reference Berg, Dickhaut and McCabe1995). The standard egoistic economic model can be adjusted to yield a model that fits these empirical findings by amending the assumption that people are exclusively pursuing their material self-interest to the assumption that people care about fairness considerations (Rabin Reference Rabin1993; Fehr and Schmidt Reference Fehr and Schmidt1999; Bolton and Ockenfels Reference Bolton and Ockenfels2000; Charness and Rabin Reference Charness and Rabin2002). Simply stated, these theoretical models presuppose that people care about the distribution of the gains. They hence challenge the egoistic assumption in standard economic models. In effect, they stipulate a transformation of the payoffs, so let us refer to these as payoff transformation theories.
A conceptual clarification is in order. The scientific target of payoff transformation theories is to study what motivates people. To be more precise, these theories generally start with a material game, that is, a game that incorporates the material payoffs of the players, and then propose a transformation that turns this material game into a motivational game that takes into account some motivationally relevant factors.Footnote 1 (The egoistic assumption can then be characterized as positing that the only motivationally relevant factors are a player’s own material payoffs.) There are, then, two challenges. First, we need to rigorously characterize the various motivationally relevant factors. Mathematical models have been introduced to characterize the nature of these factors and these models arguably provide an intelligible and systematic explication of the factors. Second, given such a rigorous theory, one can accurately formulate the behavioural predictions and, consequently, determine which experimental evidence would validate or falsify the proposition that a given set of motivational factors influence people’s behaviour.
Another strand of literature emerged in ethics, more specifically, in utilitarian theory, which focused on the observation that a group may together fail to promote deontic utility even if each player performs an individual action that promotes deontic utility (Hodgson Reference Hodgson1967; Regan Reference Regan1980). Stated differently, it is perceivable that all the members of a group fulfil their individual moral obligation even though there is an alternative group action that would have benefited the group more. The problem arises when the members find themselves in a coordination problem. In recent years, these philosophical insights have been picked up and cultivated by some economists who developed the theory of team reasoning (Sugden Reference Sugden1993; Bacharach Reference Bacharach, Gold and Sugden2006). Furthermore, the theory of team reasoning has been shown to explain empirical results from a set of lab experiments regarding coordination games (Colman et al. Reference Colman, Pulford and Rose2008; Bardsley et al. Reference Bardsley, Mehta, Starmer and Sugden2010; Butler Reference Butler2012; Bardsley and Ule Reference Bardsley and Ule2017; Pulford et al. Reference Pulford, Colman, Lawrence and Krockow2017). The unorthodox feature of these models is that they challenge the individualistic assumption in rational choice theory, that is, they allow for players to conceive of a decision problem as a problem for the team rather than for themselves. A team reasoner asks herself ‘What should we do?’ as opposed to asking herself ‘What should I do?’. In effect, this induces an agency transformation.
Can these economic models be unified? A unification would help provide a rigorous model that supports both the experimental findings regarding fairness and those regarding coordination problems. However, the consensus among team reasoning theorists is that the action recommendations yielded by team reasoning cannot be explained by payoff transformations – at least, not in a credible way (Bacharach Reference Bacharach1999; Colman Reference Colman2003). I call this the incompatibility claim.
What is the importance of this incompatibility claim? First, if this incompatibility claim were true, then it would be necessary to include team reasoning theories in our theoretical toolbox in order to explain certain behavioural findings. The crucial problem arises in forms of coordination in which two or more individuals try to coordinate their actions in order to achieve a common goal. In particular, team reasoning theorists claim that payoff transformation theories cannot explain why people manage to jointly select an outcome that is best for everyone in a common-interest scenario.Footnote 2 This observation can be rephrased in two ways: the negative upshot is that payoff transformation theories are defective in that they cannot explain this finding; and, the positive upshot is an independent argument for endorsing team reasoning theories.
Second, one pivotal issue in the philosophy of the social sciences concerns whether collective intentionality and collective action can be explained in terms of standard individualistic intentional attitudes. This is an instance of the more general discussion on methodological individualism (Heath Reference Heath and Zalta2015). If the incompatibility claim were true, then this would generate a key argument for a negative answer to this issue (Tuomela Reference Tuomela2013).Footnote 3 The latter conceptual distinction is important because it may have further consequences for the central debates about the tenability of methodological individualism.Footnote 4
Alas, I argue against the incompatibility claim and demonstrate that team reasoning can be viewed as a kind of payoff transformation theory.Footnote 5 To be more precise, I show that there is a payoff transformation that yields the same behavioural predictions and action recommendations. I call this payoff transformation the theory of participatory motivations, because it indicates that people care about the group actions they participate in.
The second main goal is to compare and contrast team reasoning – and, by extension, participatory motivations – with existing payoff transformation theories. To illustrate this prospect, three well-known models from the payoff transformation literature will be investigated. The resulting insights yield three general impossibility results: a large class of payoff transformation theories recommends actions that team reasoning rules out. In other words, none of these payoff transformation theories can explain the action recommendations that are yielded by team reasoning. Hence, if payoff transformation theories wish to explain the experimental finding of coordination games, then a rather unorthodox payoff transformation is required.
The paper proceeds as follows. I start with some preliminaries regarding game theory and, in particular, explicate the notion of a material game (
![]() ${\rm{\S}}$
2). Those familiar with game theory can decide to skip most of this section; however, for the purposes of this paper it is vital to become familiar with the distinction between material payoffs and personal motivation. An introduction to some theories and models of payoff transformation (
${\rm{\S}}$
2). Those familiar with game theory can decide to skip most of this section; however, for the purposes of this paper it is vital to become familiar with the distinction between material payoffs and personal motivation. An introduction to some theories and models of payoff transformation (
![]() ${\rm{\S}}$
3) and team reasoning (
${\rm{\S}}$
3) and team reasoning (
![]() ${\rm{\S}}$
4) follows. The impossibility result and possibility result regarding the relation between payoff transformations and team reasoning are presented and discussed in
${\rm{\S}}$
4) follows. The impossibility result and possibility result regarding the relation between payoff transformations and team reasoning are presented and discussed in
![]() ${\rm{\S}}$
5. Finally, I conclude with a discussion of the empirical and theoretical ramifications of my findings.
${\rm{\S}}$
5. Finally, I conclude with a discussion of the empirical and theoretical ramifications of my findings.
2. Game theory and material games
Starting with the seminal work by von Neumann and Morgenstern (Reference von Neumann and Morgenstern1944), the theory of games has been further developed and applied to study a wide range of phenomena and topics. The theory provides a useful framework for thinking about interdependent decision problems (Schelling Reference Schelling1960). I will begin by considering an example and its game-theoretical model. Then, I set the stage for the remainder of the paper by providing some definitions and conceptual clarifications.
Ultimatum game. Suppose a proposer and a responder bargain about the distribution of a cake. For simplicity’s sake, let us suppose that there are two available distributions: the 80–20 split and the 50–50 split. The proposer can propose a particular distribution of the cake and the responder can either decide to accept the offer, or to reject it. If the responder accepts the offer, then each gets their allocation. If, however, the responder rejects the offer, both will get nothing; see Figure 1.Footnote 6
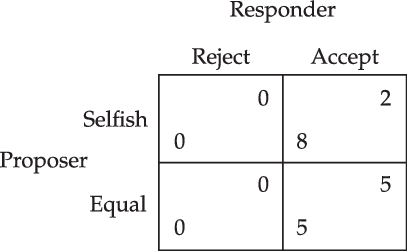
Figure 1. Ultimatum game.
This example highlights the two fundamental components of a game-theoretical model: the game form and the utilities. A game form involves a finite set N of individual agents. Each individual agent i in N has a non-empty and finite set
![]() ${A_i}$
of available individual actions. The Cartesian product
${A_i}$
of available individual actions. The Cartesian product
![]() ${ \times _{i \in N}}{A_i}$
of all the individual agents’ sets of actions gives the full set A of action profiles.Footnote 7 The outcome function o selects for each action profile the resulting outcome
${ \times _{i \in N}}{A_i}$
of all the individual agents’ sets of actions gives the full set A of action profiles.Footnote 7 The outcome function o selects for each action profile the resulting outcome
![]() $o(a)$
from the set of possible outcomes X. These games are generally called normal-form games or strategic-form games.Footnote 8
$o(a)$
from the set of possible outcomes X. These games are generally called normal-form games or strategic-form games.Footnote 8
Definition 1 (Game Form). A game form S is a tuple
![]() $\langle N,({A_i}),X,o\rangle $
, where N is a finite set of individual agents, for each agent i in N it holds that
$\langle N,({A_i}),X,o\rangle $
, where N is a finite set of individual agents, for each agent i in N it holds that
![]() ${A_i}$
is a non-empty and finite set of actions available to agent i, X is a finite set of possible outcomes, and o is an outcome function that assigns to each action profile a an outcome
${A_i}$
is a non-empty and finite set of actions available to agent i, X is a finite set of possible outcomes, and o is an outcome function that assigns to each action profile a an outcome
![]() $o(a) \in X$
.
$o(a) \in X$
.
Let me mention some additional notational conventions and some derivative concepts. I use
![]() ${a_i}$
and
${a_i}$
and
![]() ${a'_i}$
as variables for individual actions in the set
${a'_i}$
as variables for individual actions in the set
![]() ${A_i}$
and I use a and
${A_i}$
and I use a and
![]() $a'$
as variables for action profiles in the set A. For each group
$a'$
as variables for action profiles in the set A. For each group
![]() ${\cal G} \subseteq N$
the set
${\cal G} \subseteq N$
the set
![]() ${A_{\cal G}}$
of group actions that are available to group
${A_{\cal G}}$
of group actions that are available to group
![]() ${\cal G}$
is defined as the Cartesian product
${\cal G}$
is defined as the Cartesian product
![]() ${ \times _{i \in {\cal G}}}{A_i}$
of all the individual group members’ sets of actions. I use
${ \times _{i \in {\cal G}}}{A_i}$
of all the individual group members’ sets of actions. I use
![]() ${a_{\cal G}}$
and
${a_{\cal G}}$
and
![]() ${a'_{\cal G}}$
as variables for group actions in the set
${a'_{\cal G}}$
as variables for group actions in the set
![]() ${A_{\cal G}}$
(
${A_{\cal G}}$
(
![]() $ = { \times _{i \in {\cal G}}}{A_i}$
). Moreover, if
$ = { \times _{i \in {\cal G}}}{A_i}$
). Moreover, if
![]() ${a_{\cal G}}$
is a group action of group
${a_{\cal G}}$
is a group action of group
![]() ${\cal G}$
and if
${\cal G}$
and if
![]() ${\cal F} \subseteq {\cal G}$
, then
${\cal F} \subseteq {\cal G}$
, then
![]() ${a_{\cal F}}$
denotes the subgroup action that is
${a_{\cal F}}$
denotes the subgroup action that is
![]() ${\cal F}$
’s component subgroup action of the group action
${\cal F}$
’s component subgroup action of the group action
![]() ${a_{\cal G}}$
. I let
${a_{\cal G}}$
. I let
![]() $ - {\cal G}$
denote the relative complement
$ - {\cal G}$
denote the relative complement
![]() $N - {\cal G}$
. Finally, if
$N - {\cal G}$
. Finally, if
![]() ${\cal F} \cap {\cal G} = \emptyset $
, then any two group actions
${\cal F} \cap {\cal G} = \emptyset $
, then any two group actions
![]() ${a_{\cal F}}$
and
${a_{\cal F}}$
and
![]() ${a_{\cal G}}$
can be combined into a group action
${a_{\cal G}}$
can be combined into a group action
![]() $({a_{\cal F}},{a_{\cal G}}) \in {A_{{\cal F} \cup {\cal G}}}$
.
$({a_{\cal F}},{a_{\cal G}}) \in {A_{{\cal F} \cup {\cal G}}}$
.
It is typically assumed that a utility function
![]() ${u_i}$
of a given individual i assigns to each outcome x a value
${u_i}$
of a given individual i assigns to each outcome x a value
![]() ${u_i}(x)$
. However, we will assume that such a utility function
${u_i}(x)$
. However, we will assume that such a utility function
![]() ${u_i}$
assigns to each action profile a a value
${u_i}$
assigns to each action profile a a value
![]() ${u_i}(a)$
. It is easy to see that the latter is a generalization of the former. Let us call a utility function
${u_i}(a)$
. It is easy to see that the latter is a generalization of the former. Let us call a utility function
![]() ${u_i}$
outcome-based if and only if for every
${u_i}$
outcome-based if and only if for every
![]() $a,b \in A$
it holds that
$a,b \in A$
it holds that
![]() ${u_i}(a) = {u_i}(b)$
if
${u_i}(a) = {u_i}(b)$
if
![]() $o(a) = o(b)$
. The take-home message is that this generalization allows for non-outcome-based utility functions.
$o(a) = o(b)$
. The take-home message is that this generalization allows for non-outcome-based utility functions.
A utility function can be used to represent many different things. It is typically used by rational choice theorists to represent the preferences of an agent, or to represent the revealed preferences of an agent (Okasha (Reference Okasha2016) provides a useful discussion on decision-theoretical interpretations of utility). But this is not the only available interpretation. Deontic logicians, for instance, use a (typically, binary) utility function to represent a single moral code (see Hilpinen (Reference Hilpinen1971), or, more specifically, Føllesdal and Hilpinen (Reference Føllesdal, Hilpinen and Hilpinen1971: 15–19)). Depending on the interpretation of the utility function, derived game-theoretical notions should be interpreted differently. The value that an agent i’s utility function
![]() ${u_i}$
assigns to an action profile is usually given by a real number, which straightforwardly induces a comparison between action profiles, viz. a yields more utility than b according to
${u_i}$
assigns to an action profile is usually given by a real number, which straightforwardly induces a comparison between action profiles, viz. a yields more utility than b according to
![]() ${u_i}$
if and only if
${u_i}$
if and only if
![]() ${u_i}(a) \gt {u_i}(b)$
. Depending on the interpretation of the utility function this means that (i) agent i prefers a over b, (ii) agent i always chooses a over b, or (iii) a is deontically better than b.
${u_i}(a) \gt {u_i}(b)$
. Depending on the interpretation of the utility function this means that (i) agent i prefers a over b, (ii) agent i always chooses a over b, or (iii) a is deontically better than b.
My focus is on two different interpretations: the personal material payoff, denoted by
![]() ${m_i}$
, and personal motivation, denoted by
${m_i}$
, and personal motivation, denoted by
![]() ${u_i}$
. That is,
${u_i}$
. That is,
![]() ${m_i}(a) \gt {m_i}(b)$
means that agent i’s material payoff that results from action profile a is higher than that associated with b; and
${m_i}(a) \gt {m_i}(b)$
means that agent i’s material payoff that results from action profile a is higher than that associated with b; and
![]() ${u_i}(a) \gt {u_i}(b)$
means that agent i cares more about action profile a than about b (the latter will be important in
${u_i}(a) \gt {u_i}(b)$
means that agent i cares more about action profile a than about b (the latter will be important in
![]() ${\rm{\S}}$
3).
${\rm{\S}}$
3).
Definition 2 (Material Game). A material game S is a tuple
![]() $\langle N,({A_i}),X,o,({m_i})\rangle $
, where
$\langle N,({A_i}),X,o,({m_i})\rangle $
, where
![]() $\langle N,({A_i}),X,o\rangle $
is a game form, and for each agent i in N it holds that
$\langle N,({A_i}),X,o\rangle $
is a game form, and for each agent i in N it holds that
![]() ${m_i}$
is a material payoff function that assigns to each action profile a in A a value
${m_i}$
is a material payoff function that assigns to each action profile a in A a value
![]() ${m_i}(a) \in {\mathbb {R}}$
.
${m_i}(a) \in {\mathbb {R}}$
.
Rational choice theory has produced many solution concepts. I will follow the dominant practice in the social sciences and focus on the Nash equilibrium, named after John Nash (Reference Nash1950, Reference Nash1951). Stated simply, Ann and Bob are in a Nash equilibrium if Ann is making the best decision she can, given Bob’s actual decision, and Bob is making the best decision he can, given Ann’s actual decision. Likewise, a group of agents are in a Nash equilibrium if each agent is making the best decision she can, given the actual decisions of the others. A Nash equilibrium is typically taken to represent a state in which no one has an incentive to deviate, given the choices of the others.Footnote 9 To illustrate, the Nash equilibria in the discussed ultimatum game is (selfish, accept).
Definition 3 (Nash Equilibrium). Let
![]() $S = \langle N,({A_i}),X,o,({u_i})\rangle $
be a game. Then an action profile a is a Nash equilibrium if and only if for each agent i in N and for every
$S = \langle N,({A_i}),X,o,({u_i})\rangle $
be a game. Then an action profile a is a Nash equilibrium if and only if for each agent i in N and for every
![]() ${b_i} \in {A_i}$
it holds that
${b_i} \in {A_i}$
it holds that
![]() ${u_i}(a) \ge {u_i}({b_i},{a_{ - i}})$
.
${u_i}(a) \ge {u_i}({b_i},{a_{ - i}})$
.
3. Payoff transformation theories
It is well known that standard economic models are unable to explain some trivial examples of human decision-making. For instance, the traditional theory of self-interested rational individuals cannot explain, at least not satisfactorily, why people vote, pay their taxes, or sacrifice their own prospects in favour of those of a peer. Following psychological research dating back to the 1950s, experimental economists started to gather further evidence in the 1980s and 1990s showing that people diverge from purely self-interest and these findings could be replicated. These observations include the fact that people are willing to sacrifice part of their own material payoff to the benefit of another.
To illustrate this conflict between empirical evidence and theoretical predictions, recall the ultimatum game (Figure 1). As noted before, the only Nash equilibrium is (selfish, accept). This means that standard egoistic rational choice theory predicts that proposers will choose the selfish distribution and that responders will accept this offer. The experimental evidence, in contrast, shows that people generally choose the fair distribution and that responders choose to reject selfish offers. Both empirical findings are at odds with the predictions of standard rational choice theory.
To explain these empirical results, economists have proposed several theoretical models that take considerations of fairness and reciprocity into account.Footnote 10 For example, Ernst Fehr and Klaus Schmidt write:
We model fairness as self-centered inequity aversion. Inequity aversion means that people resist inequitable outcomes; i.e., they are willing to give up some material payoff to move in the direction of more equitable outcomes. Inequity aversion is self-centered if people do not care per se about inequity that exists among other people but are only interested in the fairness of their own material payoff relative to the payoff of others. (Fehr and Schmidt Reference Fehr and Schmidt1999: 819)
These and similar models have been used to fruitfully explain various empirical findings (Rabin Reference Rabin1993; Bolton and Ockenfels Reference Bolton and Ockenfels2000; Fehr and Schmidt Reference Fehr, Schmidt, Kolm and Ythier2006).Footnote 11 It is instructive to look a bit more closely at the theoretical models proposed by Fehr and Schmidt (Reference Fehr and Schmidt1999). For my current purposes, it will be helpful to do so on the basis of, what I call, motivational games:
Definition 4 (Motivational Game). A motivational game S is a tuple
![]() $\langle N,$
$\langle N,$
![]() $({A_i}),$
$({A_i}),$
![]() $X,$
$X,$
![]() $o,$
$o,$
![]() $({m_i}),$
$({m_i}),$
![]() $({u_i})\rangle $
, where
$({u_i})\rangle $
, where
![]() $\langle N,$
$\langle N,$
![]() $({A_i}),$
$({A_i}),$
![]() $X,$
$X,$
![]() $o,$
$o,$
![]() $({m_i})\rangle $
is a material game, and for each agent i in N it holds that
$({m_i})\rangle $
is a material game, and for each agent i in N it holds that
![]() ${u_i}$
is a personal motivation function that assigns to each action profile a in A a value
${u_i}$
is a personal motivation function that assigns to each action profile a in A a value
![]() ${u_i}(a) \in {\mathbb {R}}$
.Footnote 12
${u_i}(a) \in {\mathbb {R}}$
.Footnote 12
The models proposed by Fehr and Schmidt (Reference Fehr and Schmidt1999) incorporate the intuition that people dislike inequitable outcomes. This experience of inequity works in both directions: people feel disadvantageous inequity if they are worse off than others; and they feel advantageous inequity if they are better off than others. These two experiences are modelled using two parameters:
![]() ${\alpha _i}$
represents agent i’s disutility from disadvantageous inequality;
${\alpha _i}$
represents agent i’s disutility from disadvantageous inequality;
![]() ${\beta _i}$
represents agent i’s disutility from advantageous inequality. The motivation function is then given by the following equation:
${\beta _i}$
represents agent i’s disutility from advantageous inequality. The motivation function is then given by the following equation:
where
![]() $|N|$
is the cardinality of the set of individual agents, and it is assumed that
$|N|$
is the cardinality of the set of individual agents, and it is assumed that
![]() ${\beta _i} \le {\alpha _i}$
and
${\beta _i} \le {\alpha _i}$
and
![]() $0 \le {\beta _i} \lt 1$
. The resulting motivation function thus reflects a combination of personal material payoff and relative material payoff.
$0 \le {\beta _i} \lt 1$
. The resulting motivation function thus reflects a combination of personal material payoff and relative material payoff.
These payoff transformations are related to the socio-psychological literature on social value orientations (SVO) (Deutsch Reference Deutsch1949; Messick and McClintock Reference Messick and McClintock1968; McClintock Reference McClintock1972, see Van Lange Reference Van Lange1999; Murphy and Ackermann Reference Murphy and Ackermann2014 for more recent work), where different SVO types are represented by linear payoff transformations. Let us consider the simple two-player case involving agent i and j. It is common to distinguish four basic SVO types: agent i has an individualistic value orientation if
![]() ${u_i} = {m_i}$
;Footnote 13 agent i has an altruistic value orientation if
${u_i} = {m_i}$
;Footnote 13 agent i has an altruistic value orientation if
![]() ${u_i} = {m_j}$
; agent i has a cooperative value orientation if
${u_i} = {m_j}$
; agent i has a cooperative value orientation if
![]() ${u_i} = {m_i} + {m_j}$
; and, lastly, agent i has a competitive value orientation if
${u_i} = {m_i} + {m_j}$
; and, lastly, agent i has a competitive value orientation if
![]() ${u_i} = {m_i} - {m_j}$
.Footnote 14
${u_i} = {m_i} - {m_j}$
.Footnote 14
Moreover, Van Lange (Reference Van Lange1999) has introduced the so-called egalitarian social value orientation, which readily corresponds to inequity aversion in the model by Fehr and Schmidt (Reference Fehr and Schmidt1999). In its most general form, social value orientations can be modelled using motivation functions given by the following equation:
 $$\eqalign{{u_i}(x) = {w_i} \cdot {m_i}(x) + {\Sigma _{j \ne i}}{w_j} \cdot {m_j}(x) \cr - {\alpha _i}{1 \over {|N| - 1}}{\Sigma _{j \ne i}}\max [{m_j}(x) - {m_i}(x),0] \cr - {\beta _i}{1 \over {|N| - 1}}{\Sigma _{j \ne i}}\max [{m_i}(x) - {m_j}(x),0]}$$
$$\eqalign{{u_i}(x) = {w_i} \cdot {m_i}(x) + {\Sigma _{j \ne i}}{w_j} \cdot {m_j}(x) \cr - {\alpha _i}{1 \over {|N| - 1}}{\Sigma _{j \ne i}}\max [{m_j}(x) - {m_i}(x),0] \cr - {\beta _i}{1 \over {|N| - 1}}{\Sigma _{j \ne i}}\max [{m_i}(x) - {m_j}(x),0]}$$
where
![]() $|N|$
is the cardinality of the set of individual agents, it is assumed that
$|N|$
is the cardinality of the set of individual agents, it is assumed that
![]() ${\beta _i} \le {\alpha _i}$
and
${\beta _i} \le {\alpha _i}$
and
![]() $0 \le {\beta _i} \lt 1$
, and it is assumed that
$0 \le {\beta _i} \lt 1$
, and it is assumed that
![]() ${w_i} \in {\mathbb {R}}$
and
${w_i} \in {\mathbb {R}}$
and
![]() ${w_j} \in \mathbb {R}}$
for every
${w_j} \in \mathbb {R}}$
for every
![]() $j \in N$
. These motivation functions indicate that people may care about their own material payoff, the material payoff of others and that they may dislike inequitable outcomes. Let us call these SVO motivation functions.
$j \in N$
. These motivation functions indicate that people may care about their own material payoff, the material payoff of others and that they may dislike inequitable outcomes. Let us call these SVO motivation functions.
It should be noted that these particular payoff transformation theories are outcome-based. That is, the postulated motivation functions only depend on the outcome, not on the way that outcome came about. There are other payoff transformation theories that involve motivation functions that are not outcome-based. In the literature on social preferences, these are commonly called intention-based, since these motivation functions are based on whether others’ actions are performed with kind or unkind intentions.Footnote 15 Let us briefly go over the general components of the models introduced by Rabin (Reference Rabin1993) (also see Dufwenberg and Kirchsteiger Reference Dufwenberg and Kirchsteiger2004; Falk and Fischbacher Reference Falk and Fischbacher2006; Segal and Sobel Reference Segal and Sobel2007).
Matthew Rabin writes that we need a model that incorporates three facts:
-
(A) People are willing to sacrifice their own material well-being to help those who are being kind.
-
(B) People are willing to sacrifice their own material well-being to punish those who are being unkind.
-
(C) Both motivations (A) and (B) have a greater effect on behavior as the material cost of sacrificing becomes smaller. (Rabin Reference Rabin1993: 1282)
Without going into unnecessary technical details,Footnote 16 it is helpful to note that this payoff transformation relies on so-called kindness functions. Given an action profile, these kindness functions can be used to indicate how kind player i is being towards player j. To illustrate this notion of kindness, recall the ultimatum game, which is depicted in Figure 1. Let us consider the action profile (selfish, accept). The kindness of the proposer toward the responder is a function of the set of personal material payoffs of the responder that could result when the responder conforms to (selfish, accept). The idea is that, given the responder’s choice to accept, the proposer effectively chooses between the selfish distribution of (8,2) and the equal distribution of (5,5). In particular, this means that the proposer decides to choose the distribution that yields a material payoff of 2 for the responder whereas she could have chosen a distribution that would have yielded a material payoff of 5 for the responder. This means that the proposer is being unkind to the responder.
Let us formalize some of these ideas to illustrate a few properties of these kindness functions. It suffices for our purposes to focus on two-player games. Consider a two-player material game S and a particular profile
![]() $a = ({a_1},{a_2})$
. As indicated before, given the action profile a, the kindness of player
$a = ({a_1},{a_2})$
. As indicated before, given the action profile a, the kindness of player
![]() $1$
towards player
$1$
towards player
![]() $2$
can be determined by considering the set of action profiles that are compatible with
$2$
can be determined by considering the set of action profiles that are compatible with
![]() $2$
’s choice, that is,
$2$
’s choice, that is,
![]() ${A^{conf}}({a_2}): = \{ b \in A|{b_2} = {a_2}\} $
, and their associated material payoffs
${A^{conf}}({a_2}): = \{ b \in A|{b_2} = {a_2}\} $
, and their associated material payoffs
![]() ${M_2^{conf}}({a_2}): = \{ {m_2}(b)|b \in {A^{conf}}({a_2})\} $
. First, note that this means the kindness of player
${M_2^{conf}}({a_2}): = \{ {m_2}(b)|b \in {A^{conf}}({a_2})\} $
. First, note that this means the kindness of player
![]() $1$
towards player
$1$
towards player
![]() $2$
at action profile a does not depend on action profiles in which all players deviate from a. That is, the kindness at a depends only on action profiles where some players conform to a. Second, in particular, if
$2$
at action profile a does not depend on action profiles in which all players deviate from a. That is, the kindness at a depends only on action profiles where some players conform to a. Second, in particular, if
![]() ${m_2}(a)$
is maximal in
${m_2}(a)$
is maximal in
![]() ${M_2^{conf}}({a_2})$
, then player
${M_2^{conf}}({a_2})$
, then player
![]() $1$
is not being unkind to player
$1$
is not being unkind to player
![]() $2$
. Third, if
$2$
. Third, if
![]() ${m_2}(a)$
is minimal in
${m_2}(a)$
is minimal in
![]() ${M_2^{conf}}({a_2})$
, then player
${M_2^{conf}}({a_2})$
, then player
![]() $1$
is not being kind to player
$1$
is not being kind to player
![]() $2$
.Footnote 17 These observations will be crucial for the impossibility result and the accompanying discussion in
$2$
.Footnote 17 These observations will be crucial for the impossibility result and the accompanying discussion in
![]() ${\rm{\S}}$
5.
${\rm{\S}}$
5.
The resulting personal motivation functions in Rabin’s framework incorporate material payoffs and a notion of reciprocity in terms of kindness functions. These models indicate that players wish to treat others in kind, that is, player i wishes to treat player j kindly only if j treats her kindly and vice versa. This means that the personal motivation functions are not purely outcome-based. After all, their personal motivation depends on how the other agents treat them.
4. Team reasoning
The idea of team reasoning originates from ethical theories of utilitarianism.Footnote 18 The core idea of team reasoning is that a member of a group asks herself ‘What should we do?’ rather than ‘What should I do?’. Team reasoning hence relies on a we-perspective. This means that a team reasoner first considers the group actions available to the group, assesses these group actions in terms of their consequences, finds the group action that best furthers their common or collective interests, and then chooses her component of that group action.
To explain team reasoning in more detail and to contrast it with traditional rational choice theory, let us consider the Hi-Lo game depicted in Figure 2. Team reasoning theorists claim that traditional rational choice theory does not adequately address the Hi-Lo game. It seems that (high, high) is the only rational solution, but the players have no reason for preferring one action over the other if they are guided by traditional rational choice theory. Let us see why. The Hi-Lo game contains two Nash equilibria: (high, high) and (low, low).Footnote 19 In particular, the action profile (low, low) represents a state of equilibrium in which no one has an incentive to deviate from performing her component individual action, given that everyone else performs their respective part.
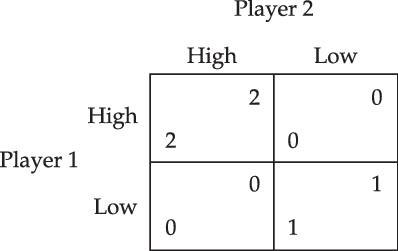
Figure 2. The Hi-Lo game.
As a response to this multiplicity, one may want to refine the Nash equilibria by appealing to the Pareto dominance of (high, high) over (low, low) in order to select the Nash equilibrium (high, high) as the only rational solution.Footnote 20 There are two problems with such a solution. First, what is the status of the Pareto principle in standard rational choice theory? Hollis and Sugden (Reference Sugden1993: 13) argue that the Pareto principle “is a principle of rationality only to players who conceive of themselves as a team, but not for players who do not”. It is therefore plausible that the rationalization of the Pareto principle requires a departure from the central assumption in rational choice theory that agency is only invested in individuals. Second, in any case, such a (Pareto-dominant) Nash equilibrium only captures a possible status-quo: if everyone expected the others to play their part in the Nash equilibrium, then they would have a reason to do the same. It hence gives only a conditional recommendation and triggers an infinite regress of reasons. I need not fully rehearse the problems for traditional rational choice theory here, but the gist of the paradox should be clear at this point: the theory does not rule out (low, low) and fails to select (high, high) as the unique solution to the Hi-Lo game.Footnote 21 This is not merely a theoretical glitch, but it is also at odds with experimental evidence that people generally choose high.Footnote 22 This inadequate response to the Hi-Lo game by traditional rational choice theory stands to be corrected, which is what team reasoning (as studied by Bacharach, Sugden, and Gold) has been designed for.Footnote 23
For our current purposes, it suffices to investigate the question of whether payoff transformation theories can rule out (low, low) in the Hi-Lo game. This investigation will take centre stage in the next section. Notice that this question is more narrow than the question of whether rational choice theory can rule out (low, low).
Bacharach (Reference Bacharach, Gold and Sugden2006: Ch. 1) and Sugden (Reference Sugden2000: sec. 2, 3, 7 and 8) argue that traditional rational choice theory needs to be augmented with a collectivistic reasoning method to successfully address the Hi-Lo game. Team reasoning theorists appeal to the reasoning process by which an individual agent reasons about what to do. An individual agent engaged in team reasoning “works out the best feasible combination of actions for all the members of her team, then does her part in it” (Bacharach Reference Bacharach, Gold and Sugden2006: 121). In the Hi-Lo game, this reasoning goes as follows: the row player first identifies (high, high) as the best combination of individual actions that they can perform and then decides to perform her part in that combination, i.e. high. Similar reasoning prescribes high for the column player. Team reasoning therefore entails that high is the only rational option, and selects (high, high) as the only rational outcome. It hence solves the Hi-Lo game.
To help clarify the scope and limits of my study, let me briefly discuss two questions that are relevant for operationalizing team reasoning. First, what are team preferences (in contrast to individual preferences)? Team reasoning is generally taken to presuppose team preferences that are used to determine the best combination of individual actions that the team can perform (see Bacharach Reference Bacharach1999; Sugden Reference Sugden2000). There are only a handful of proposals in the literature that specify what this team preference generally involves. Sugden (Reference Sugden2010, Reference Sugden2011, Reference Sugden2015) seems to rely on a notion of mutual advantage or benefit.Footnote 24 Bacharach (Reference Bacharach, Gold and Sugden2006: 59) on the other hand, hypothesizes that a team reasoner “ranks all act-profiles, using a Paretian criterion”.Footnote 25 I follow the trend in team reasoning and will suppose that the team preference is given. The benefit of doing so is that the framework could incorporate any theory of team preferences.
It is helpful to add that team reasoning, interpreted strictly, does not operate on the Hi-Lo game, as represented in Figure 2, since the game only shows the individual preferences. Because team reasoning relies on team preferences, we need to make some assumption regarding these team preferences. It is nonetheless uncontroversial that the group prefers (high, high) over (low, low). Team reasoning thus yields a convincing argument for choosing high in the Hi-Lo game.Footnote 26
Second, how can the theory of team reasoning be extended to apply to a greater variety of problems – not just the Hi-Lo game?Footnote 27 In this essay, I will focus on interdependent decision problems where the team preferences determine a unique best group action.Footnote 28 The application of team reasoning is unambiguous in these cases and the Hi-Lo game indicates that traditional rational choice theory can fall short even in these idealized cases. The main reasons for excluding cases where there are multiple best group actions are that team reasoning theorists have only sparingly addressed these cases and it is hard to formulate general desiderata that we would like our decision theory to satisfy.Footnote 29
The discussion of the Hi-Lo game and these two questions for team reasoning should help the reader grasp the idea of team reasoning. Now, let me set forth a simple model of team reasoning. A team game extends a material game by adding participation states and team preferences.Footnote 30 The participation states of the agents are specified by a function P that assigns to each agent i the team
![]() $P(i) \subseteq N$
in which she is active. For each group
$P(i) \subseteq N$
in which she is active. For each group
![]() ${\cal G}$
in the range of P, the team preference function
${\cal G}$
in the range of P, the team preference function
![]() ${v_{\cal G}}$
assigns to each action profile a in A a value
${v_{\cal G}}$
assigns to each action profile a in A a value
![]() ${v_{\cal G}}(a) \in {\mathbb {R}}$
. This illustrates that a given team game presupposes that individuals team reason from the perspective of the team they are active in and rely on the associated team preference.
${v_{\cal G}}(a) \in {\mathbb {R}}$
. This illustrates that a given team game presupposes that individuals team reason from the perspective of the team they are active in and rely on the associated team preference.
Definition 5 (Team Game). A team game S is a tuple
![]() $\langle N,({A_i}),X,o,({m_i}),P,({v_{\cal G}})\rangle $
, where
$\langle N,({A_i}),X,o,({m_i}),P,({v_{\cal G}})\rangle $
, where
![]() $\langle N,({A_i}),X,o,({m_i})\rangle $
is a material game, P assigns to each agent i in N the team
$\langle N,({A_i}),X,o,({m_i})\rangle $
is a material game, P assigns to each agent i in N the team
![]() $P(i) \subseteq N$
that she is active in, and
$P(i) \subseteq N$
that she is active in, and
![]() ${v_{\cal G}}$
is the team preference function that assigns to each action profile a in A a value
${v_{\cal G}}$
is the team preference function that assigns to each action profile a in A a value
![]() ${v_{\cal G}}(a) \in {\mathbb {R}}$
, one for each group
${v_{\cal G}}(a) \in {\mathbb {R}}$
, one for each group
![]() ${\cal G}$
in the range of P.Footnote 31
${\cal G}$
in the range of P.Footnote 31
As indicated before, team reasoning theorists assume that players do not reason in line with traditional rational choice theory – at least in cases where the agent is active in a non-singleton team. Let us specify how team reasoning works in a given team game S. An agent i first determines the group action for the group
![]() $P(i)( = {\cal G})$
that best promotes the team preference
$P(i)( = {\cal G})$
that best promotes the team preference
![]() ${v_{\cal G}}$
and then selects the individual action that is her part in that group action. Under the assumption that there is a unique best group action, team reasoning yields a unique individual action for each individual.
${v_{\cal G}}$
and then selects the individual action that is her part in that group action. Under the assumption that there is a unique best group action, team reasoning yields a unique individual action for each individual.
To illustrate, let us see how team games might explain the choice of high in the Hi-Lo game. First, one could postulate the participation function that assigns to each of the two individuals the team consisting of both. Second, one can postulate that the team preference function is identical to the personal material payoff functions. The resulting team game is depicted in Figure 3. This team game supports the conclusion that each individual will choose high. Let us see why. An individual will first determine the group action that best promotes the team preferences. In this particular case the group action (high, high) does so. Then, she selects the individual action that is her part of this group action, which yields high.
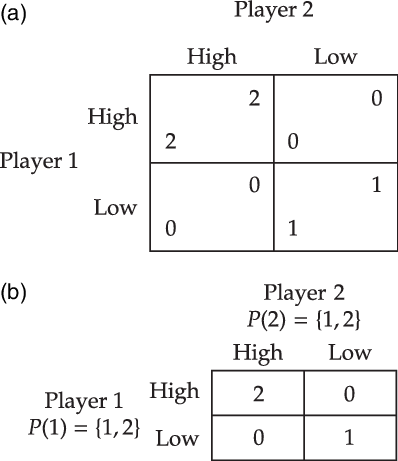
Figure 3. An illustration of a team game that yields high in the material Hi-Lo game. (a) The material Hi-Lo game. (b) Team game of the material Hi-Lo game, where the numbers represent the team preference of the group
![]() $\{ 1,2\} $
.
$\{ 1,2\} $
.
5. Team reasoning as a payoff transformation theory
What is the relation between team reasoning and payoff transformation theories? It should be noted that team games generalize motivational games. That is, for each motivational game S we can simply define a corresponding team game by setting
![]() $P(i) = \{ i\} $
for every agent i in N and where the team preference function is identical to the personal motivation function, that is,
$P(i) = \{ i\} $
for every agent i in N and where the team preference function is identical to the personal motivation function, that is,
![]() ${v_i} = {u_i}$
. This entails that every motivational game can be viewed as a team game. Therefore, every payoff transformation theory can be incorporated as an agency transformation theory. Note, however, that the corresponding team game only involves participation states that indicate that each individual agent is active in the singleton ‘team’ consisting of only herself. It is thus a bit of a conceptual stretch to call such a team game an agency transformation. After all, the vital revision that team reasoning proposes is that people need not be active in their personal singleton ‘team’.
${v_i} = {u_i}$
. This entails that every motivational game can be viewed as a team game. Therefore, every payoff transformation theory can be incorporated as an agency transformation theory. Note, however, that the corresponding team game only involves participation states that indicate that each individual agent is active in the singleton ‘team’ consisting of only herself. It is thus a bit of a conceptual stretch to call such a team game an agency transformation. After all, the vital revision that team reasoning proposes is that people need not be active in their personal singleton ‘team’.
Nevertheless, a payoff transformation theory may be implemented in the theory of team reasoning to yield predicted or observed behaviour in experimental settings. Consequently, experimental evidence for a particular payoff transformation theory is compatible with team reasoning. This should not come as a surprise, since team reasoning allows for both a payoff transformation and an agency transformation.
5.1. The impossibility result
What about the other direction, that is, can team reasoning be viewed as a payoff transformation? It is important to note that payoff transformation theories use rationality principles from orthodox rational choice theory to derive the predicted or observed behaviour in experimental settings. That is, these theories only change the utilities; the action recommendations then follow from standard rationality principles.
The theory of team reasoning, in contrast to payoff transformation theories, revises the rationality principles of traditional rational choice theory by adopting a new reasoning method. It is often claimed that team reasoning differs from certain payoff transformation theories:
[T]eam reasoning differs from, and is more powerful than, adopting the group’s objective and then reasoning in the standard individualistic way. (Bacharach Reference Bacharach1999: 144)Footnote 32
Team reasoning is inherently non-individualistic and cannot be derived from transformational models of social value orientation. (Colman Reference Colman2003: 151)
Two games play an important role in the theory of team reasoning: the Hi-Lo game (see Figure 2) and the famous prisoner’s dilemma (see Figure 5a). In particular, team reasoning theorists claim that payoff transformation theories cannot explain the choice of high in the Hi-Lo game. In general, they advance the claim that the action recommendations of team reasoning cannot be explained by payoff transformations – at least, not in a satisfactory way. Call this the incompatibility claim. For example, Natalie Gold and Robert Sugden write:
By using the concept of agency transformation, [team reasoning] is able to explain the choice of high in Hi-Lo. Existing theories of payoff transformation cannot do this. It is hard to see how any such theory could credibly make (high, high) the unique solution of Hi-Lo….
For Bacharach, the “strongest argument of all” in support of [the team-reasoning account] of cooperation [in the prisoner’s dilemma] is that the same theory predicts the choice of high in Hi-Lo games. (Bacharach Reference Bacharach, Gold and Sugden2006: 173–174)Footnote 33
In contrast to this consensus among team reasoning theorists, I will prove that every team game can be associated with a motivational game in such a way that they yield the same action recommendations. In other words, my results demonstrate that we do not need to transform both the payoffs and the unit of agency, rather, it suffices to transform only the payoffs.Footnote 34 I call this particular payoff transformation the theory of participatory motivations (see
![]() ${\rm{\S}}$
5.2 for more details).
${\rm{\S}}$
5.2 for more details).
My discussion and results demonstrate that participatory motivations are able to explain both the choice of high in the Hi-Lo game and the choice to cooperate in the prisoner’s dilemma. Before getting there, it will be helpful to ask whether team reasoning can be captured by the payoff transformations proposed by Fehr and Schmidt (Reference Fehr and Schmidt1999), theories of social value orientations, and Rabin (Reference Rabin1993), as discussed in
![]() ${\rm{\S}}$
3. The interrogation of these payoff transformation theories will yield three general impossibility results.
${\rm{\S}}$
3. The interrogation of these payoff transformation theories will yield three general impossibility results.
Given the key role of the Hi-Lo game, it will be central to my investigation of payoff transformation theories. As a preliminary remark, the argument in
![]() ${\rm{\S}}$
4 demonstrated that traditional rational choice theory fails to select high as the unique solution to the Hi-Lo game. It is therefore vital to remark that the same argument applies to any payoff transformation that transforms the material game associated with the Hi-Lo game into a motivational game in which the action profiles are assigned similar values by the personal motivation functions. More precisely, to rule out low for player 1, payoff transformation theories need to yield a motivation function
${\rm{\S}}$
4 demonstrated that traditional rational choice theory fails to select high as the unique solution to the Hi-Lo game. It is therefore vital to remark that the same argument applies to any payoff transformation that transforms the material game associated with the Hi-Lo game into a motivational game in which the action profiles are assigned similar values by the personal motivation functions. More precisely, to rule out low for player 1, payoff transformation theories need to yield a motivation function
![]() ${u_1}$
that satisfies
${u_1}$
that satisfies
![]() ${u_1}$
(high, low)
${u_1}$
(high, low)
![]() $ \gt {u_1}$
(low, low). Moreover, to explain the choice of high for player 1, the motivation function
$ \gt {u_1}$
(low, low). Moreover, to explain the choice of high for player 1, the motivation function
![]() ${u_1}$
needs to satisfy
${u_1}$
needs to satisfy
![]() ${u_1}$
(high, high)
${u_1}$
(high, high)
![]() $ \gt {u_1}$
(low, high).
$ \gt {u_1}$
(low, high).
Let us start with investigating the model proposed by Fehr and Schmidt (Reference Fehr and Schmidt1999). Consider the material Hi-Lo game. Recall that team reasoning yields the action recommendation to play high – at least, given the team game depicted in Figure 3. Is it possible to construct a motivational game, using payoff transformations proposed by Fehr and Schmidt (Reference Fehr and Schmidt1999), that yields the same prescription? In particular, as noted before, this induces the requirement that
![]() ${u_1}$
(high, low)
${u_1}$
(high, low)
![]() $ \gt {u_1}$
(low, low). Hence, this requirement entails that
$ \gt {u_1}$
(low, low). Hence, this requirement entails that
![]() ${u_1}$
can decrease even if the personal material payoff increases while the relative material payoff remains unchanged. This is a strange proposition. It is, indeed, easy to verify that this is incompatible with the theory proposed by Fehr and Schmidt (Reference Fehr and Schmidt1999). In fact, the resulting personal motivation function is the same as the material payoff function in the Hi-Lo game regardless of the values of the parameters
${u_1}$
can decrease even if the personal material payoff increases while the relative material payoff remains unchanged. This is a strange proposition. It is, indeed, easy to verify that this is incompatible with the theory proposed by Fehr and Schmidt (Reference Fehr and Schmidt1999). In fact, the resulting personal motivation function is the same as the material payoff function in the Hi-Lo game regardless of the values of the parameters
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. In particular, for any values of the parameters
$\beta $
. In particular, for any values of the parameters
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
it will be the case that the resulting motivational game does not rule out (low, low). This is the inspiration for the first impossibility result.
$\beta $
it will be the case that the resulting motivational game does not rule out (low, low). This is the inspiration for the first impossibility result.
To generalize this observation, consider a particular motivational game
![]() $S'$
. Let us use
$S'$
. Let us use
![]() ${A^{eq}}$
to denote the set of action profiles that yield an equal distribution of material payoffs, that is,
${A^{eq}}$
to denote the set of action profiles that yield an equal distribution of material payoffs, that is,
![]() ${A^{eq}}$
is the set
${A^{eq}}$
is the set
![]() $\{ a \in A|$
for every
$\{ a \in A|$
for every
![]() $i,j \in N$
it holds that
$i,j \in N$
it holds that
![]() ${m_i}(a) = {m_j}(a)\} $
. Given an agent i, we propose to call her personal motivation function equity-Pareto if it satisfies the following criterion:
${m_i}(a) = {m_j}(a)\} $
. Given an agent i, we propose to call her personal motivation function equity-Pareto if it satisfies the following criterion:
-
(EP) for any action profiles
 $a,b \in {A^{eq}}$
it holds that
$a,b \in {A^{eq}}$
it holds that
 ${u_i}(a) \gt {u_i}(b)$
if and only if for every agent j it holds that
${u_i}(a) \gt {u_i}(b)$
if and only if for every agent j it holds that
 ${m_j}(a) \gt {m_j}(b)$
.
${m_j}(a) \gt {m_j}(b)$
.
In other words, agent i prefers the outcome associated with profile a more than the one associated with b if action profile a yields a higher material payoff for all agents and both a and b yield an equal distribution of material payoffs. That is, the personal motivations respect the Pareto principle on the set of action profiles that yield equal distributions. Or, equivalently, they can only violate the Pareto principle on action profiles that yield unequal distributions. It is easy to verify that the model proposed by Fehr and Schmidt (Reference Fehr and Schmidt1999) validates this equity-Pareto principle. Moreover, it seems that any plausible payoff transformation theory that relies only on considerations of equality will conform to this principle.
Theorem 1 (First Impossibility Result). Let S be the material game associated with the Hi-Lo game. Let
![]() $S'$
be a motivational game that is based on S. Suppose the personal motivation functions are equity-Pareto. Then
$S'$
be a motivational game that is based on S. Suppose the personal motivation functions are equity-Pareto. Then
![]() $S'$
does not rule out (low, low).
$S'$
does not rule out (low, low).
Proof. Observe that
![]() ${A^{eq}} = A = \{ $
(high, high), (high, low), (low, high), (low, low)
${A^{eq}} = A = \{ $
(high, high), (high, low), (low, high), (low, low)
![]() $\} $
. Note that
$\} $
. Note that
![]() ${u_1}$
(low, low)
${u_1}$
(low, low)
![]() $ \gt {u_1}$
(high, low), since these action profiles each yield equal distributions of material payoff and (low, low) Pareto dominates (high, low). Hence, (low, low) is a Nash equilibrium in the motivational game
$ \gt {u_1}$
(high, low), since these action profiles each yield equal distributions of material payoff and (low, low) Pareto dominates (high, low). Hence, (low, low) is a Nash equilibrium in the motivational game
![]() $S'$
.
$S'$
. ![]()
The following is an immediate consequence of this impossibility result. Consider a particular payoff transformation theory. If this payoff transformation theory conforms to the equity-Pareto principle, then the action recommendations yielded by this payoff transformation theory are different from those yielded by team reasoning. This finding resonates with the incompatibility claim.
Let us proceed to theories of social value orientation. It can be shown that whenever a given SVO motivation function is compatible with choosing high, then it is also compatible with low. In other words, there exists no SVO motivation function that yields the same action recommendations as team reasoning in the Hi-Lo game.Footnote 35
Theorem 2 (Second Impossibility Result). Let S be the material game associated with the Hi-Lo game. Let
![]() $S'$
be a motivational game that is based on S. Suppose the personal motivation functions are SVO motivation functions. Then,
$S'$
be a motivational game that is based on S. Suppose the personal motivation functions are SVO motivation functions. Then,
![]() $S'$
cannot be compatible with (high, high) while ruling out (low, low).
$S'$
cannot be compatible with (high, high) while ruling out (low, low).
Proof. Observe that
![]() ${A^{eq}} = A = \{ $
(high, high), (high, low), (low, high), (low, low)
${A^{eq}} = A = \{ $
(high, high), (high, low), (low, high), (low, low)
![]() $\} $
. Therefore, for any profile a in A it holds that
$\} $
. Therefore, for any profile a in A it holds that
![]() ${u_1}(a)$
can be given by
${u_1}(a)$
can be given by
![]() $({w_1} + {w_2}) \cdot {m_1}(a)$
, where
$({w_1} + {w_2}) \cdot {m_1}(a)$
, where
![]() ${{w_1},{w_2} \in {\mathbb {R}}}$
. Assume that
${{w_1},{w_2} \in {\mathbb {R}}}$
. Assume that
![]() $S'$
is compatible with (high, high). Then, we must have
$S'$
is compatible with (high, high). Then, we must have
![]() ${u_1}$
(high, high)
${u_1}$
(high, high)
![]() $ \ge {u_1}$
(low, high) and, therefore,
$ \ge {u_1}$
(low, high) and, therefore,
![]() $({w_1} + {w_2}) \ge 0$
. However, this entails that
$({w_1} + {w_2}) \ge 0$
. However, this entails that
![]() ${u_1}$
(low, low)
${u_1}$
(low, low)
![]() $ \ge {u_1}$
(high, low). Hence, (low, low) is a Nash equilibrium in the motivational game
$ \ge {u_1}$
(high, low). Hence, (low, low) is a Nash equilibrium in the motivational game
![]() $S'$
.
$S'$
. ![]()
Let us now interrogate the model of Rabin (Reference Rabin1993).Footnote 36 To investigate its application to the material Hi-Lo game, we need to investigate whether at (low, low) player
![]() $2$
is willing to sacrifice her material payoff in order to help or punish the other. To do so, we need to first determine whether player
$2$
is willing to sacrifice her material payoff in order to help or punish the other. To do so, we need to first determine whether player
![]() $1$
is being kind to player
$1$
is being kind to player
![]() $2$
at (low, low). As noted in
$2$
at (low, low). As noted in
![]() ${\rm{\S}}$
3, we need to consider the set of action profiles consisting of (high, low) and (low, low), and the associated material payoffs for player
${\rm{\S}}$
3, we need to consider the set of action profiles consisting of (high, low) and (low, low), and the associated material payoffs for player
![]() $2$
, which are
$2$
, which are
![]() $0$
and
$0$
and
![]() $1$
, respectively. Given this set of action profiles, player
$1$
, respectively. Given this set of action profiles, player
![]() $2$
’s material payoff is highest at (low, low). This entails that player
$2$
’s material payoff is highest at (low, low). This entails that player
![]() $1$
is not being unkind to player
$1$
is not being unkind to player
![]() $2$
at the action profile (low, low) and it might even be that player
$2$
at the action profile (low, low) and it might even be that player
![]() $1$
is being kind to player
$1$
is being kind to player
![]() $2$
(depending on the exact details of the kindness functions). Hence, player
$2$
(depending on the exact details of the kindness functions). Hence, player
![]() $2$
might be willing to sacrifice her own material well-being in order to help player
$2$
might be willing to sacrifice her own material well-being in order to help player
![]() $1$
. However, given player
$1$
. However, given player
![]() $1$
’s action, player
$1$
’s action, player
![]() $2$
cannot improve player
$2$
cannot improve player
![]() $1$
’s material payoff. That is,
$1$
’s material payoff. That is,
![]() ${m_1}$
(low, low)
${m_1}$
(low, low)
![]() $ \gt {m_1}$
(low, high). Hence, player
$ \gt {m_1}$
(low, high). Hence, player
![]() $2$
is not motivated to deviate from (low, low). Similar reasoning shows that player
$2$
is not motivated to deviate from (low, low). Similar reasoning shows that player
![]() $1$
is also not so motivated. In other words, Rabin’s proposed motivational game does not rule out (low, low).
$1$
is also not so motivated. In other words, Rabin’s proposed motivational game does not rule out (low, low).
To generalize this observation, take an arbitrary material game S and consider a particular motivational game
![]() $S'$
. Recall that, for any action profile a, Rabin’s kindness function that assesses whether agent i was kind to agent j only relies on the set of action profiles where agent j conforms to a, that is,
$S'$
. Recall that, for any action profile a, Rabin’s kindness function that assesses whether agent i was kind to agent j only relies on the set of action profiles where agent j conforms to a, that is,
![]() ${A^{conf}}({a_j})$
. In particular, for the profile (low, low) this means that the kindness functions of players
${A^{conf}}({a_j})$
. In particular, for the profile (low, low) this means that the kindness functions of players
![]() $1$
and
$1$
and
![]() $2$
only rely on the set
$2$
only rely on the set
![]() $\{ $
(high, low), (low, high), (low, low)
$\{ $
(high, low), (low, high), (low, low)
![]() $\} $
, that is, they do not rely on (high, high). Moreover, this means that any agent’s kindness function at most relies on the set of action profiles
$\} $
, that is, they do not rely on (high, high). Moreover, this means that any agent’s kindness function at most relies on the set of action profiles
![]() ${A^{conf}}(a): = \{ b \in A|$
there is an agent i such that
${A^{conf}}(a): = \{ b \in A|$
there is an agent i such that
![]() ${a_i} = {b_i}\} $
. The set
${a_i} = {b_i}\} $
. The set
![]() ${A^{conf}}(a)$
can be thought of as those action profiles that may result from partial conformity to a – as opposed to full-scale deviation.
${A^{conf}}(a)$
can be thought of as those action profiles that may result from partial conformity to a – as opposed to full-scale deviation.
Consider any action profile a such that each player’s material payoff at a is higher than her material payoff associated with any other action profile in
![]() ${A^{conf}}(a)$
. Then, none of the agents is being unkind to others while some might even be kind to others (depending on the specific details of the kindness functions). In light of Rabin’s first fact, the agents might be motivated to sacrifice their own material payoff in order to help others. However, under this condition, no agent can improve any other agent’s material payoff. Moreover, under this assumption, no agent can improve her own material payoff. Hence, the three facts that Rabin wishes to accommodate entail that, under these circumstances, no player is willing to deviate from a.
${A^{conf}}(a)$
. Then, none of the agents is being unkind to others while some might even be kind to others (depending on the specific details of the kindness functions). In light of Rabin’s first fact, the agents might be motivated to sacrifice their own material payoff in order to help others. However, under this condition, no agent can improve any other agent’s material payoff. Moreover, under this assumption, no agent can improve her own material payoff. Hence, the three facts that Rabin wishes to accommodate entail that, under these circumstances, no player is willing to deviate from a.
Given an agent i, we propose to call her personal motivation function partial-conformity-Pareto if it satisfies the following criterion:
(PCP) for any action profiles
![]() $a,b \in A$
it holds that
$a,b \in A$
it holds that
![]() ${u_i}(a) \ge {u_i}(b)$
if
${u_i}(a) \ge {u_i}(b)$
if
-
(i)
 $b \in {A^{conf}}(a)$
, and
$b \in {A^{conf}}(a)$
, and -
(ii) for every agent j it holds that
 ${m_j}(a) = \mathop {\max }\nolimits_{c \in {A^{conf}}(a)} {m_j}(c)$
.
${m_j}(a) = \mathop {\max }\nolimits_{c \in {A^{conf}}(a)} {m_j}(c)$
.
In other words, no agent assigns a higher utility to action profile b than to a if action profile b partially conforms to a and a Pareto dominates all of the action profiles that partially conform to it. It should be clear that Rabin’s models validate this principle. Moreover, it seems that any plausible payoff transformation theory that relies only on considerations of kindness that involve partial conformity will incorporate this principle.
Theorem 3 (Third Impossibility Result). Let S be the material game associated with the Hi-Lo game. Let
![]() $S'$
be a motivational game that is based on S. Suppose the personal motivation functions are partial-conformity-Pareto. Then
$S'$
be a motivational game that is based on S. Suppose the personal motivation functions are partial-conformity-Pareto. Then
![]() $S'$
does not rule out (low, low).
$S'$
does not rule out (low, low).
Proof. Note that
![]() ${A^{conf}}$
((low, low))
${A^{conf}}$
((low, low))
![]() $ = \{ $
(high, low), (low, high), (low, low)
$ = \{ $
(high, low), (low, high), (low, low)
![]() $\} $
and note that for each player j it holds that
$\} $
and note that for each player j it holds that
![]() ${m_j}$
(low, low)
${m_j}$
(low, low)
![]() $ = \mathop {\max }\nolimits_{c \in {A^{conf}}{\rm{((low,low))}}} {m_j}(c)$
. Hence,
$ = \mathop {\max }\nolimits_{c \in {A^{conf}}{\rm{((low,low))}}} {m_j}(c)$
. Hence,
![]() ${u_1}$
(low, low)
${u_1}$
(low, low)
![]() $ \ge {u_1}$
(high, low), since conditions (PCP)(i) and (PCP)(ii) hold for (low, low) and (high, low). Hence, (low, low) is a Nash equilibrium in the motivational game
$ \ge {u_1}$
(high, low), since conditions (PCP)(i) and (PCP)(ii) hold for (low, low) and (high, low). Hence, (low, low) is a Nash equilibrium in the motivational game
![]() $S'$
.
$S'$
. ![]()
Consider any payoff transformation theory that endorses the partial-conformity-Pareto principle. Then the action recommendations yielded by this payoff transformation theory are different from those yielded by team reasoning. This, again, concurs with the incompatibility claim.
What have we learnt from these impossibility results? Instead of drawing the conclusion that the individualistic assumption in rational choice theory needs to be abandoned in order to explain that (high, high) is the unique solution of the Hi-Lo game, I take this to mean that the agents need to care about more than equality and reciprocity. The general principles underlying these impossibility results can help to establish that other payoff transformation theories are also incompatible with team reasoning. Moreover, these principles indicate that a rather unorthodox payoff transformation theory is required for explaining why low is ruled out. After all, any payoff transformation that conforms to (EP) or (PCP) will be compatible with low and, as a consequence, will be incompatible with team reasoning.
5.2. The possibility result
I demonstrate that team reasoning can be viewed as a payoff transformation that incorporates the intuition that people care about the group actions they participate in.Footnote 37 In particular, my proposal reflects the following two stylized ideas:
-
(*) People might be willing to sacrifice their own material well-being to do their part in a collective act, where their part is defined as the individual action they ought to perform if the group is to be successful in realizing a shared goal.
-
(**) Motivation (
 $ * $
) has greater effect on behaviour as the material cost of sacrificing becomes smaller.
$ * $
) has greater effect on behaviour as the material cost of sacrificing becomes smaller.
Team reasoning solves the Hi-Lo game by relying on a team game. In this section, the aim is to demonstrate that there are ways to define a motivational game on the basis of a given team game. It may be hard to determine which individual acts would qualify as doing your part in a collective act. For instance, in cases where agent i is active in a team that does not include all the agents she interacts with, it may be hard to determine which group action best promotes the team’s utility. Moreover, there may be cases where there are multiple ways to achieve a certain goal and the group is indifferent between each of these. However, when agent i is active in the team consisting of all the agents, then the best group actions are exactly those group actions that yield the highest team utility. In the remainder of this section, we therefore restrict our attention to team games that uniquely identify the best group actions.
Although there are multiple ways to incorporate the idea that agents care about the group actions they participate in, for our current purposes it suffices to show that there is a motivation function that yields the same action recommendations as team reasoning does. For simplicity’s sake, we assume that each individual agent i is active in the team consisting of all the agents – that is,
![]() $P(i) = N$
. Let us introduce some notation to rigorously characterize the idea that agents care about the group actions they participate in. Recall that
$P(i) = N$
. Let us introduce some notation to rigorously characterize the idea that agents care about the group actions they participate in. Recall that
![]() ${A^{conf}}({a_i})$
is the set of action profiles that are compatible with agent i’s choice
${A^{conf}}({a_i})$
is the set of action profiles that are compatible with agent i’s choice
![]() ${a_i}$
. Let
${a_i}$
. Let
![]() $V_i^{conf}({a_i}): = \{ {v_{\cal G}}(b)|P(i) = {\cal G}$
and
$V_i^{conf}({a_i}): = \{ {v_{\cal G}}(b)|P(i) = {\cal G}$
and
![]() $b \in {A^{conf}}({a_i})\} $
denote the team utilities that are associated with the team that agent i is active in and with the action profiles in
$b \in {A^{conf}}({a_i})\} $
denote the team utilities that are associated with the team that agent i is active in and with the action profiles in
![]() ${A^{conf}}({a_i})$
. Consider the following motivation function:
${A^{conf}}({a_i})$
. Consider the following motivation function:
where
![]() ${\gamma _i},{\delta _i} \ge 0$
,
${\gamma _i},{\delta _i} \ge 0$
,
![]() ${\gamma _i}$
represents the utility from the agent’s material payoff, and
${\gamma _i}$
represents the utility from the agent’s material payoff, and
![]() ${\delta _i}$
represents the utility from the group actions one participates in. (The subscript i for the parameters
${\delta _i}$
represents the utility from the group actions one participates in. (The subscript i for the parameters
![]() $\gamma $
and
$\gamma $
and
![]() $\delta $
is suppressed in case the omission does not give rise to ambiguity.) Let us call these participatory motivation functions.Footnote 38
$\delta $
is suppressed in case the omission does not give rise to ambiguity.) Let us call these participatory motivation functions.Footnote 38
The benefit of including both the parameters
![]() $\gamma $
and
$\gamma $
and
![]() $\delta $
is that we can empirically test the trade-off between the material payoff and the ‘participatory’ utility. After all, it seems highly implausible that people will always sacrifice their own material payoff in order to promote participatory utility. Whereas team reasoning theorists typically invoke a strict dichotomy between individualistic reasoning and team reasoning, the proposed participatory motivations allow for a more gradual picture where participatory utility can outweigh material payoffs – without neglecting material payoffs altogether.Footnote 39
$\delta $
is that we can empirically test the trade-off between the material payoff and the ‘participatory’ utility. After all, it seems highly implausible that people will always sacrifice their own material payoff in order to promote participatory utility. Whereas team reasoning theorists typically invoke a strict dichotomy between individualistic reasoning and team reasoning, the proposed participatory motivations allow for a more gradual picture where participatory utility can outweigh material payoffs – without neglecting material payoffs altogether.Footnote 39
To illustrate the participatory motivation function for the Hi-Lo game, consider Figure 4 which depicts the participatory motivational game that is associated with the team game of the Hi-Lo game (Figure 3). It should be clear that (low, low) fails to be a Nash equilibrium in the participatory motivational game if and only if
![]() $\delta \gt \gamma $
. That is, participatory motivations rule out low if and only if the agents care more about the group actions they participate in than about their material payoff. Hence, under these assumptions, standard rationality principles can be applied to the participatory motivational game of the Hi-Lo game to yield high. More precisely, the application of the standard rationality principles in this participatory motivational game rules out low, as desired.
$\delta \gt \gamma $
. That is, participatory motivations rule out low if and only if the agents care more about the group actions they participate in than about their material payoff. Hence, under these assumptions, standard rationality principles can be applied to the participatory motivational game of the Hi-Lo game to yield high. More precisely, the application of the standard rationality principles in this participatory motivational game rules out low, as desired.
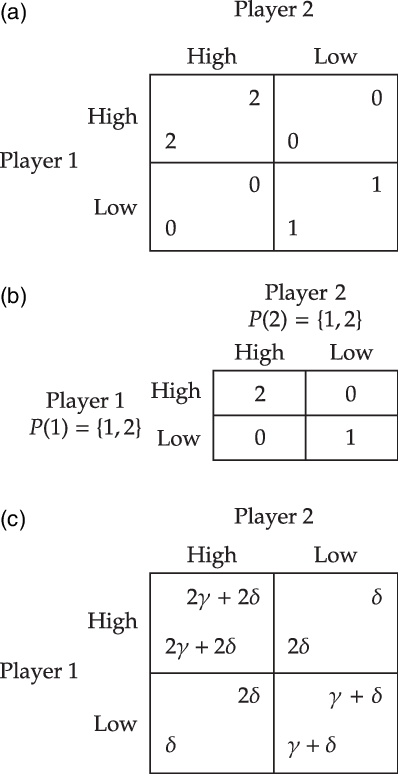
Figure 4. An illustration of the participatory motivational game associated with the Hi-Lo game. (a) Material game of the Hi-Lo game. (b) The team game associated with the Hi-Lo game. (c) The participatory motivational game of the Hi-Lo game.
Theorem 4 (Possibility Result for Hi-Lo). Let S be the material game associated with the Hi-Lo game. Then there exists a motivational game
![]() $S'$
, that is associated with S, such that (high, high) is the only Nash equilibrium in
$S'$
, that is associated with S, such that (high, high) is the only Nash equilibrium in
![]() $S'$
.
$S'$
.
Proof. Consider the motivational game depicted in Figure 4 with
![]() $\delta \gt \gamma $
. In the resulting motivational game, only (high, high) is a Nash equilibrium.
$\delta \gt \gamma $
. In the resulting motivational game, only (high, high) is a Nash equilibrium. ![]()
Before generalizing this possibility result, let us elaborate on one way to interpret the values assigned by the participatory motivations in the Hi-Lo game. Consider P1 in the participatory motivational game with
![]() $\gamma = 0$
and
$\gamma = 0$
and
![]() $\delta = 1$
(see Figure 4). What makes it the case that her utility is 1 at (low, high) while it is 2 at (high, low)? Her utilities could be taken to describe what it would feel like for her to end up in one of the cells of the game matrix. Although there is no distinction in the actual outcome, I suggest that the distinction be thought of as follows. At (high, low) P1 thinks of herself as having counterfactually participated in (high, high), while at (low, high) she thinks of herself as having counterfactually participated in (low, low). In other words, the difference between these outcomes is that P1 either sees herself as doing her part in the collective act (high, high) or as doing her part in the collective act (low, low). Since (high, high) yields a higher team utility than (low, low), her participatory utility is higher at (high, low) than at (low, high).Footnote 40
$\delta = 1$
(see Figure 4). What makes it the case that her utility is 1 at (low, high) while it is 2 at (high, low)? Her utilities could be taken to describe what it would feel like for her to end up in one of the cells of the game matrix. Although there is no distinction in the actual outcome, I suggest that the distinction be thought of as follows. At (high, low) P1 thinks of herself as having counterfactually participated in (high, high), while at (low, high) she thinks of herself as having counterfactually participated in (low, low). In other words, the difference between these outcomes is that P1 either sees herself as doing her part in the collective act (high, high) or as doing her part in the collective act (low, low). Since (high, high) yields a higher team utility than (low, low), her participatory utility is higher at (high, low) than at (low, high).Footnote 40
It is important to realize that participatory motivations can explain cooperation in the prisoner’s dilemma. To illustrate this fact, consider the game-theoretical model of the prisoner’s dilemma in Figure 5a. To apply the theory of participatory motivations, let me add the assumption that the team utility is given by the sum of the individual material payoff.Footnote 41 That is,
![]() ${v_N}(a) = {\Sigma _{i \in N}}{m_i}(a)$
. The participatory motivational game associated with prisoner’s dilemma is depicted in Figure 5.
${v_N}(a) = {\Sigma _{i \in N}}{m_i}(a)$
. The participatory motivational game associated with prisoner’s dilemma is depicted in Figure 5.
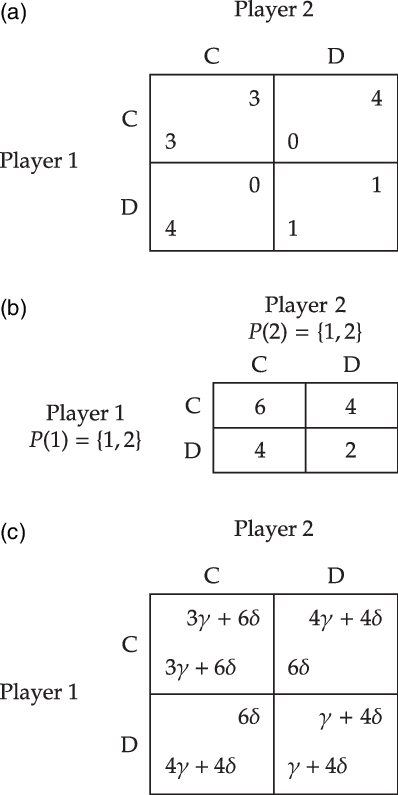
Figure 5. An illustration of the participatory motivational game associated with the prisoner’s dilemma. (a) Material game of the prisoner’s dilemma. (b) The team game associated with the prisoner’s dilemma. (c) The participatory motivational game of the prisoner’s dilemma.
In the participatory motivational game associated with the prisoner’s dilemma, it is easy to see that (C, C) is the only Nash equilibrium if and only if the following inequalities obtain:
Hence, the agent cooperates if and only if
![]() $2\delta \gt \gamma $
. That is, under these idealized assumptions, an agent cooperates if and only if she cares less than twice as much about her material payoff than about the group actions she participates in. The model thus demonstrates that an agent will cooperate depending on the (agent-specific) trade-off between material self-interest and participatory utility, i.e. depending on the exact values of
$2\delta \gt \gamma $
. That is, under these idealized assumptions, an agent cooperates if and only if she cares less than twice as much about her material payoff than about the group actions she participates in. The model thus demonstrates that an agent will cooperate depending on the (agent-specific) trade-off between material self-interest and participatory utility, i.e. depending on the exact values of
![]() ${\gamma _i}$
and
${\gamma _i}$
and
![]() ${\delta _i}$
. It is an advantage that participatory motivations can be used to explain cooperation in the prisoner’s dilemma.
${\delta _i}$
. It is an advantage that participatory motivations can be used to explain cooperation in the prisoner’s dilemma.
Let us generalize the possibility result to team games that include a unique best group action. For this class of team games, team reasoning can be subsumed under participatory motivations. In particular, in these scenarios, we can prove that team reasoning yields the same action recommendations as participatory motivation functions with
![]() $\gamma = 0$
and
$\gamma = 0$
and
![]() $\delta \gt 0$
.
$\delta \gt 0$
.
Theorem 5 (Possibility Result). Let S be a material game. Let
![]() ${S_T}$
be a team game based on S, and let i in N be an agent. Suppose that
${S_T}$
be a team game based on S, and let i in N be an agent. Suppose that
![]() $P(i) = N$
and suppose that
$P(i) = N$
and suppose that
![]() ${v_N}$
yields a unique best group action among those in A. Let
${v_N}$
yields a unique best group action among those in A. Let
![]() ${a^ * } \in A$
be the unique best group action, and let
${a^ * } \in A$
be the unique best group action, and let
![]() ${S_P}$
be any participatory motivational game with
${S_P}$
be any participatory motivational game with
![]() $\gamma = 0$
and
$\gamma = 0$
and
![]() $\delta \gt 0$
. Then,
$\delta \gt 0$
. Then,
![]() ${a^ * }$
is the only Nash equilibrium in
${a^ * }$
is the only Nash equilibrium in
![]() ${S_P}$
.
${S_P}$
.
Proof. Take any action profiles
![]() $a,b \in A$
with
$a,b \in A$
with
![]() ${a_i} = a_i^ * $
and
${a_i} = a_i^ * $
and
![]() ${b_i} \ne a_i^ * $
. Hence
${b_i} \ne a_i^ * $
. Hence
![]() ${a^ * } \in {A^{conf}}({a_i})$
and
${a^ * } \in {A^{conf}}({a_i})$
and
![]() ${a^ * } \notin\ {A^{conf}}({b_i})$
. Since
${a^ * } \notin\ {A^{conf}}({b_i})$
. Since
![]() ${a^ * }$
is the unique best group action, it holds that
${a^ * }$
is the unique best group action, it holds that
![]() $\max V_i^{conf}({a_i}) \gt \max V_i^{conf}({b_i})$
. Since
$\max V_i^{conf}({a_i}) \gt \max V_i^{conf}({b_i})$
. Since
![]() $\gamma = 0$
, we get
$\gamma = 0$
, we get
![]() $u_i^{\max }(a) = \delta \cdot \max V_i^{conf}({a_i}) \gt \delta \cdot \max V_i^{conf}({b_i}) = u_i^{\max }(b)$
. It follows that
$u_i^{\max }(a) = \delta \cdot \max V_i^{conf}({a_i}) \gt \delta \cdot \max V_i^{conf}({b_i}) = u_i^{\max }(b)$
. It follows that
![]() $a_i^ * $
strictly dominates any other available individual action in the participatory motivation game. Therefore,
$a_i^ * $
strictly dominates any other available individual action in the participatory motivation game. Therefore,
![]() ${a^ * }$
is the only Nash equilibrium in
${a^ * }$
is the only Nash equilibrium in
![]() ${S_P}$
.
${S_P}$
. ![]()
In other words, the associated participatory motivational game
![]() ${S_P}$
prescribes each player to perform the individual action that is her component in the best group action that is available to the team she is active in. Or, equivalently, the participatory motivations rule out any individual action that is not her component in the best group action.
${S_P}$
prescribes each player to perform the individual action that is her component in the best group action that is available to the team she is active in. Or, equivalently, the participatory motivations rule out any individual action that is not her component in the best group action.
It immediately follows that the action recommendations yielded by team reasoning in
![]() ${S_T}$
are the same as those yielded by standard rational choice theory in
${S_T}$
are the same as those yielded by standard rational choice theory in
![]() ${S_P}$
. Hence, the action recommendations of team reasoning can be equally well explained by a payoff transformation. Or, equivalently, it shows that an important part of team reasoning can be reduced to traditional individualistic reasoning with a particular motivation. So, the effects of the agency transformation in team reasoning can be simulated by a payoff transformation.
${S_P}$
. Hence, the action recommendations of team reasoning can be equally well explained by a payoff transformation. Or, equivalently, it shows that an important part of team reasoning can be reduced to traditional individualistic reasoning with a particular motivation. So, the effects of the agency transformation in team reasoning can be simulated by a payoff transformation.
To clarify, it is an open question whether the general possibility result (Theorem 5) demonstrates that participatory motivations entirely exclude any form of collective reasoning. After all, the payoff transformations rely on the team game and, in particular, on the team utilities. If these team utilities can only be obtained via team reasoning, then the corresponding participatory motivations would require team reasoning. Given the lack of consensus on what team utilities are, it is plausible that whether these participatory motivations exclude team reasoning depends on the details of the particular account of team utilities.
One of the main justifications for team reasoning is that it advances cooperative behaviour in Hi-Lo games. Whether the cooperative incentives in the material Hi-Lo game actually lead to team reasoning is not at issue. Team reasoning sets out to address what makes high the only rational option. As such, the theory of participatory motivations is on an equal footing. After all, the action recommendations resulting from team reasoning coincide with those resulting from participatory motivations in the Hi-Lo game. This justification for the team-reasoning account of cooperation therefore transfers to the theory of participatory motivations.
The previous theorem can be viewed as generalizing this justification for the theory of participatory motivations beyond the Hi-Lo game. The result establishes that whenever there is a unique best group action, then players with certain participatory motivations successfully pick out this best group action. Hence, the team-reasoning account of cooperation is on a par with the theory of participatory motivations with regard to guaranteeing successful cooperation in these scenarios.
The main possibility result entails that there is a payoff transformation theory that yields the same action recommendations as team reasoning. Therefore, if we compare theories on the basis of the action recommendations that they produce, then payoff transformations are at least as powerful as team reasoning. In other words, the action recommendations yielded by team reasoning can be derived from payoff transformation models. After all, participatory motivations can fully account for the behaviour predicted by team reasoning. It thus seems impossible for team reasoning theorists to uphold the incompatibility claim. We discuss some options to rectify the compatibility claim in the final section.
6. Discussion
The results of team reasoning cannot be explained by the particular payoff transformations of Fehr and Schmidt (Reference Fehr and Schmidt1999), nor by those involving social value orientations, nor by those of Rabin (Reference Rabin1993). More generally, I have shown that team reasoning cannot be explained by a wide class of payoff transformation theories (Theorems 1, 2 and 3). In contrast to this negative result, I have shown that there is a payoff transformation theory, which relies on participatory motivations, that does yield the same action recommendations as team reasoning (Theorems 4 and 5). This provides evidence against the incompatibility claim, which states that team reasoning cannot be derived from payoff transformation theories – at least, not in a credible way.
Before stepping back and drawing more general conclusions, let me briefly mention several properties of these participatory motivations. First, participatory motivations are process-oriented rather than outcome-based. That is, they incorporate the idea that people care not only about features of the outcome but also about how that outcome came about. In other words, it is conceivable that someone’s utility differs between two identical outcomes if they were produced in a different manner. Second, participatory motivations may evaluate a given player’s actions differently depending on the concurrent actions of the others rather than depending on the past actions of others or on the beliefs regarding the actions of others. In other words, it involves instantaneous reciprocity rather than sequential reciprocity or belief-based reciprocity.Footnote 42 Lastly, participatory motivations provide a simple model that allows for trade-offs between self-interest and team reasoning concerns (the latter is represented by the participatory utility).
With regard to the incompatibility claim, my results show that to validate this claim, team reasoning theorists need to go beyond the behavioural realm and, for example, include mental constructs in their theoretical and empirical explanandum. After all, the theory of participatory motivations is able to explain the behavioural predictions of team reasoning. It may be helpful to point out that the realm of mental constructs could include beliefs, expectations, preferences, motivations, sentiments, and perhaps even personal identity. To theoretically validate the incompatibility claim, one could try to argue that payoff transformation theories are unable to explain both what makes (high, high) rational and explain certain sets of beliefs and sentiments.
Let me supplement this observation with an example. In his recent book, Sugden (Reference Sugden2018: Ch. 9) discusses the ‘paradox of trust’ (also see Isoni and Sugden (Reference Isoni and Sugden2019)). To illustrate this paradox, consider the normal-form representation of a trust game in Figure 6.Footnote 43 The investor’s option of sending can be interpreted as investing one unit of material payoff in a way that will generate five units. The trustee then decides on how to distribute the costs and benefits of this investment. It is therefore natural to interpret the action profile (send, return) as a practice of trust. The paradox is that “in a theory in which individuals are motivated by reciprocity, two individuals cannot have common knowledge that they will both participate in a practice of trust” (Sugden Reference Sugden2018: 222). More precisely, such common knowledge would undermine the idea that the investor’s choice of send is kind. Setting aside the question of how this paradox affects existing payoff transformation theories, it is important to note that the paradox involves a behavioural and a mental component: the paradox indicates the impossibility of a practice of trust when agents are motivated by reciprocity and commonly know that each participates. Phrased differently, these beliefs and motivations are jointly incompatible with the practice of trust.
Figure 6. Trust game.
Alternatively, team reasoning theorists might claim that its mode of reasoning cannot be reduced to that of individualistic reasoning.Footnote 44 Although I cannot say anything conclusive on this suggestion, a few remarks are in order. First, in the absence of an elaborate theory of reduction, it is hard to ascertain whether the claim is interesting nor whether it is true. Second, to empirically verify the claim, it seems like we would need methods to reliably determine the mode of reasoning that people employ. Lastly, in any case, the fact that the theory of participatory motivations yields the same action recommendations as team reasoning should be taken very seriously. After all, the most compelling argument for the team-reasoning account of cooperation concerns its action recommendations: it predicts high in the Hi-Lo game and it explains cooperation in the prisoner’s dilemma.
Another theoretical move could be to argue that the notion of participatory motivations does not cohere with other mental constructs in an agent’s psychological economy. For example, the participatory motivation suggests that an individual agent’s evaluation of an outcome that was brought about by the best group action is distinct from her evaluation of that outcome if it were brought about in a different manner. This property is not standardly included in the outcomes of a game. For instance, in his seminal contribution to decision theory, Savage (Reference Savage1954) models actions as functions from states to outcomes. So standard preferences on outcomes cannot encompass these participatory motivations. However, as we alluded to in
![]() ${\rm{\S}}$
3, within the literature on other-regarding preferences there is a wide class of payoff transformations that are process-oriented. We therefore need not revise the rationality principles of traditional rational choice theory; rather, we need to revise the assumption that motivations are outcome-based.
${\rm{\S}}$
3, within the literature on other-regarding preferences there is a wide class of payoff transformations that are process-oriented. We therefore need not revise the rationality principles of traditional rational choice theory; rather, we need to revise the assumption that motivations are outcome-based.
Lastly, I would like to emphasize that I am sympathetic to the idea of team reasoning and to the ideas of fairness and reciprocity. It may turn out that a fusion between payoff transformation theories and team reasoning is needed to find the key to cooperation. My aim should thus not be understood as an attempt to reduce one to the other. Rather, by relying on this theoretical unification, we can understand the differences more rigorously and make systematic progress towards modelling human decision-making and cooperation.
Acknowledgements
The author would like to thank the audience at the University of Tampere and would especially like to thank Jan Broersen, Nathalie Gold, Raul Hakli, Jurgis Karpus, Werner Raub, Robert Sugden and Allard Tamminga for helpful comments and stimulating discussions on this paper and related topics. The author gratefully acknowledges funding from the European Research Council (the ERC-2013-CoG project REINS, no. 616512, and the ERC-2017-CoG project SEA, no. 771074).
Hein Duijf is a postdoctoral researcher at the VU Amsterdam. His current research takes inspiration from behavioural sciences (including social psychology, economics and social sciences) and agent-based modelling to study the epistemic risks and potential benefits of group deliberation. He has a PhD in Philosophy and Artificial Intelligence from Utrecht University. This second line of scholarship embraces moral responsibility, collective agency, machine ethics and deontic reasoning.










