Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-26T08:45:58.021Z Has data issue: false hasContentIssue false
  • English
  • Français

Testing for Second-Order Stochastic Dominance of Two Distributions

Published online by Cambridge University Press:  11 February 2009

Amarjot Kaur ,
B.L.S. Prakasa Rao  and
Harshinder Singh
Amarjot Kaur
Affiliation:
Panjab University
B.L.S. Prakasa Rao
Affiliation:
Indian Statistical Institute
Harshinder Singh
Affiliation:
Panjab University
Get access Rights & Permissions [Opens in a new window]

Abstract

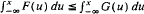A distribution function F is said to stochastically dominate another distribution function G in the second-order sense if , for all x. Second-order stochastic dominance plays an important role in economics, finance, and accounting. Here a statistical test has been constructed to test 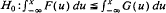, for some x ∈ [a, b], against the hypothesis 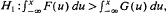, for all x ∈ [a, b], where a and b are any two real numbers. The test has been shown to be consistent and has an upper bound α on the asymptotic size. The test is expected to have usefulness for comparison of random prospects for risk averters.

Type
Articles
Information
Econometric Theory , Volume 10 , Issue 5 , December 1994 , pp. 849 - 866
Copyright
Copyright © Cambridge University Press 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bawa, V.S.Optimal rules for ordering uncertain prospects. Journal of Financial Economics 2 (1975): 95–121.CrossRefGoogle Scholar
2Bawa, V.S., Lindberg, E.B. & Rafsky, L.C.. An efficient algorithm to determine stochastic dominance admissible sets. Management Science 25 (1979): 609–622.CrossRefGoogle Scholar
3Berger, R.L., Boos, D.D. & Guess, F.M.. Tests and confidence sets for comparing two mean residual life functions. Biometrics 44 (1988): 103–115.Google Scholar
4Berger, R.L. & Sinclair, D.F.. Testing hypotheses concerning union of linear subspaces. Journal of the American Statistical Association 79 (1984): 158–163.Google Scholar
5Billingsley, P.Convergence of Probability Measures. New York: John Wiley, 1968.Google Scholar
6Chung, K.L.A Course in Probability Theory. New York: Harcourt Brace and World, 1968.Google Scholar
7Csorgo, M. & Revesz, P.. Strong Approximations in Probability and Statistics. Budapest: Academia Kiado, 1981.Google Scholar
8Deshpande, J.V. & Singh, S.P.. Ordering probability distributions in the context of economics. Proceedings of the Third Annual Conference of the Indian Society of Probability Theory and Its ApplicationsDelhi, 1981.Google Scholar
9Deshpande, J.V. & Singh, H.. Testing for second order stochastic dominance. Communications in Statistics-Theory and Methods 14 (1985): 887–893.CrossRefGoogle Scholar
10Gleser, L.J.On a theory of intersection-union tests. Institute of Mathematical Statistics, Bulletin 2 (1973): 233 (abstract).Google Scholar
11Hadar, J. & Russell, W.R.. Rules for ordering uncertain prospects. American Economic Review 59 (1969): 25–34.Google Scholar
12Hadar, J. & Russell, W.R.. Stochastic dominance and diversification. Journal of Economic Theory 3 (1971): 288–305.Google Scholar
13Hanoch, G. & Levy, H.. The efficiency analysis of choices involving risk. Review of Economic Studies 36 (1969): 335–346.CrossRefGoogle Scholar
14McFadden, D. Testing for stochastic dominance. In Fombay, T. & Seo, T.K. (eds.), Studies in Economics of Uncertainty. New York: Springer, 1989.Google Scholar
15McFadden, D., Klecan, L. & McFadden, R.. A robust test for stochastic dominance. Preprint, 1990.CrossRefGoogle Scholar
16Porter, R.B., Wart, J.R. & Ferguson, D.L.. Efficient algorithm for conducting stochastic dominance tests on large number of portfolios. Journal of Financial Quantitative Analysis 8 (1973): 71–81.Google Scholar
17Roy, S.N.Some Aspects of Multivariate Analysis. New York: Wiley, 1957.Google Scholar
18Tesfatsion, L.Stochastic dominance and maximization of expected utility. Review of Economic Studies 43 (1976): 301–315.CrossRefGoogle Scholar
19Whitmore, G.A. & Findlay, M.C.Stochastic Dominance, an Approach to Decision Making Under Risk. Health, Lexington: Mars, 1978.Google Scholar