Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hallam, Arne
1992.
A Brief Overview of Nonparametric Methods in Economics.
Northeastern Journal of Agricultural and Resource Economics,
Vol. 21,
Issue. 2,
p.
98.
Lee, Lung-Fei
1994.
Semiparametric instrumental variable estimation of simultaneous equation sample selection models.
Journal of Econometrics,
Vol. 63,
Issue. 2,
p.
341.
Lee, Lung-fei
1994.
Semiparametric two-stage estimation of sample selection models subject to Tobit-type selection rules.
Journal of Econometrics,
Vol. 61,
Issue. 2,
p.
305.
Powell, James L.
1994.
Vol. 4,
Issue. ,
p.
2443.
Lee, Lung-fei
1995.
Semiparametric maximum likelihood estimation of polychotomous and sequential choice models.
Journal of Econometrics,
Vol. 65,
Issue. 2,
p.
381.
Sepanski, Jungsywan H.
and
Lee, Lung-Fei
1995.
Semiparametric estimation of nonlinear errors-in-variables models with validation study.
Journal of Nonparametric Statistics,
Vol. 4,
Issue. 4,
p.
365.
Honoré, Bo E.
Kyriazidou, Ekaterini
and
Udry, Christopher
1997.
Estimation of Type 3 Tobit models using symmetric trimming and pairwise comparisons.
Journal of Econometrics,
Vol. 76,
Issue. 1-2,
p.
107.
Chen, Songnian
1997.
Semiparametric estimation of the Type-3 Tobit model.
Journal of Econometrics,
Vol. 80,
Issue. 1,
p.
1.
Chen, Songnian
and
Zhou, Xianbo
2011.
Semiparametric estimation of a bivariate Tobit model.
Journal of Econometrics,
Vol. 165,
Issue. 2,
p.
266.
Chen, Songnian
and
Zhou, Xianbo
2012.
Semiparametric estimation of a truncated regression model.
Journal of Econometrics,
Vol. 167,
Issue. 2,
p.
297.
Quaglione, Davide
Muscio, Alessandro
and
Vallanti, Giovanna
2015.
The two sides of academic research: do basic and applied activities complement each other?.
Economics of Innovation and New Technology,
Vol. 24,
Issue. 7,
p.
660.
Paraíba, Carolina Costa Mota
Diniz, Carlos Alberto Ribeiro
Maia, Aline de Holanda Nunes
and
Rodrigues, Lineu Neiva
2017.
Truncated location-scale non linear regression models.
Communications in Statistics - Theory and Methods,
Vol. 46,
Issue. 15,
p.
7355.
Chen, Songnian
Lu, Xun
Zhou, Xianbo
and
Zhou, Yahong
2018.
NONPARAMETRIC IDENTIFICATION AND ESTIMATION OF TRUNCATED REGRESSION MODELS WITH HETEROSKEDASTICITY.
Econometric Theory,
Vol. 34,
Issue. 3,
p.
543.
Ito, Takahiro
2021.
Binary and Ordered Response Models in Randomized Experiments.
SSRN Electronic Journal ,
Pan, Zhewen
Zhou, Xianbo
and
Zhou, Yahong
2022.
Semiparametric Estimation of a Censored Regression Model Subject to Nonparametric Sample Selection.
Journal of Business & Economic Statistics,
Vol. 40,
Issue. 1,
p.
141.
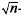 -consistent and asymptotically normal. A consistent estimate of the asymptotic covariance matrix of the estimator is provided. Monte Carlo experiments are performed to investigate some finite sample properties of the estimator.
-consistent and asymptotically normal. A consistent estimate of the asymptotic covariance matrix of the estimator is provided. Monte Carlo experiments are performed to investigate some finite sample properties of the estimator.

