Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-22T22:10:27.790Z Has data issue: false hasContentIssue false
  • English
  • Français

REGRESSION DISCONTINUITY DESIGN WITH POTENTIALLY MANY COVARIATES

Published online by Cambridge University Press:  14 February 2025

Yoichi Arai ,
Taisuke Otsu  and
Myung Hwan Seo
Yoichi Arai
Affiliation:
Waseda University
Taisuke Otsu*
Affiliation:
London School of Economics
Myung Hwan Seo
Affiliation:
Seoul National University
*
Address correspondence to Taisuke Otsu, Department of Economics, London School of Economics, London, UK; e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

This article examines high-dimensional covariates in regression discontinuity design (RDD) analysis. We introduce estimation and inference methods for the RDD models that incorporate covariate selection while maintaining stability across various numbers of covariates. The proposed methods combine a localization approach using kernel weights with 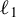$\ell _{1}$-penalization to handle high-dimensional covariates. We provide both theoretical and numerical evidence demonstrating the efficacy of our methods. Theoretically, we present risk and coverage properties for our point estimation and inference methods. Conditions are given under which the proposed estimator becomes more efficient than the conventional covariate adjusted estimator at the cost of an additional sparsity condition. Numerically, our simulation experiments and empirical examples show the robust behaviors of the proposed methods to the number of covariates in terms of bias and variance for point estimation and coverage probability and interval length for inference.

Type
ARTICLES
Information
Econometric Theory , First View , pp. 1 - 36
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This article is a developed version of a previous manuscript (https://sticerd.lse.ac.uk/dps/em/em601.pdf) inspired by a discussion with Matias Cattaneo. We are grateful to Matias Cattaneo and Sebastian Calonico for helpful comments and discussions. This research was supported by Grants-in-Aid for Scientific Research 20K01598 from the Japan Society for the Promotion of Science (Y.A.) and the ERC Consolidator Grant (SNP 615882) (T.O.). Financial support from the Center for National Competitiveness in the Institute of Economic Research of Seoul National University and the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF-2018S1A5A2A01033487) is gratefully acknowledged (M.H.S.).

References

REFERENCES

Abadie, A., & Imbens, G. W. (2006). Large sample properties of matching estimators for average treatment effects. Econometrica , 74, 253–267.CrossRefGoogle Scholar
Angrist, J. D., Imbens, G. W., & Rubin, D. B. (1996). Identification of causal effects using instrumental variables. Journal of the American Statistical Association , 91, 444–455.CrossRefGoogle Scholar
Arai, Y., Otsu, T. and Seo, M. (2021). Regression discontinuity design with potentially many covariates. Preprint, arXiv:2109.08351.Google Scholar
Armstrong, T. B., & Kolesár, M. (2018). Optimal inference in a class of regression models. Econometrica , 86, 655–683.CrossRefGoogle Scholar
Belloni, A., Chernozhukov, V., Chetverikov, D., Hansen, C., & Kato, K. (2018). High-dimensional econometrics and regularized GMM. Massachusetts Institute of Technology, Cambridge MA, Working Paper.Google Scholar
Belloni, A., Chernozhukov, V., & Hansen, C. (2014). Inference on treatment effects after selection amongst high-dimensional controls. Review of Economic Studies , 81, 608–650.CrossRefGoogle Scholar
Bickel, P. J., Ritov, Y. A., & Tsybakov, A. B. (2009). Simultaneous analysis of Lasso and Dantzig selector. Annals of Statistics , 37, 1705–1732.CrossRefGoogle Scholar
Bühlmann, P., & van de Geer, S. (2011). Statistics for high-dimensional data . Springer.CrossRefGoogle Scholar
Calonico, S., Cattaneo, M. D., & Farrell, M. H. (2018). On the effect of bias estimation on coverage accuracy in nonparametric inference. Journal of the American Statistical Association , 113, 767–779.CrossRefGoogle Scholar
Calonico, S., Cattaneo, M. D., & Farrell, M. H. (2020). Coverage error optimal confidence intervals for local polynomial regression. Preprint, arXiv:1808.01398.Google Scholar
Calonico, S., Cattaneo, M. D., Farrell, M. H., & Titiunik, R. (2017). Rdrobust: Software for regression discontinuity designs. Stata Journal , 17, 372–404.CrossRefGoogle Scholar
Calonico, S., Cattaneo, M. D., Farrell, M. H., & Titiunik, R. (2019). Regression discontinuity designs using covariates. Review of Economics and Statistics , 101, 442–451.CrossRefGoogle Scholar
Calonico, S., Cattaneo, M. D., & Titiunik, R. (2014). Robust nonparametric confidence intervals for regression-discontinuity designs. Econometrica , 82, 2295–2326.CrossRefGoogle Scholar
Calonico, S., Cattaneo, M. D., & Titiunik, R. (2015b). Rdrobust: An R package for robust inference in regression discontinuity design. R Journal , 7, 38–51.Google Scholar
Card, D., Lee, D. S., Pei, Z., & Weber, A. (2015). Inference on causal effects in a generalized regression kink design. Econometrica , 83, 2453–2483.CrossRefGoogle Scholar
Cattaneo, M. D., & Escanciano, J. C. (2017). Regression discontinuity designs: Theory and applications , in Advances in Econometrics, vol. 38, Emerald Group Publishing.CrossRefGoogle Scholar
Cattaneo, M. D., & Titiunik, R. (2022). Regression discontinuity designs. Annual Review of Economics , 14, 821–851.CrossRefGoogle Scholar
Cattaneo, M. D., Titiunik, R., & Vazquez-Bare, G. (2020). The regression discontinuity design. In Curini, L. & Franzese, R. J. (Eds.), Handbook of research methods in political science and international relations (Ch. 44, pp. 835–857). Sage Publications.Google Scholar
Fan, J., & Gijbels, I. (1992). Variable bandwidth and local linear regression smoothers. Annals of Statistics , 20, 2008–2036.CrossRefGoogle Scholar
Friedman, J. H., Hastie, T., & Tibshirani, R. (2010). Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software , 33, 1–22.CrossRefGoogle ScholarPubMed
Frölich, M., & Huber, M. (2019). Including covariates in the regression discontinuity design. Journal of Business & Economic Statistics , 37, 736–748.CrossRefGoogle Scholar
Hahn, J., Todd, P., & van der Klaauw, W. (2001). Identification and estimation of treatment effects with a regression-discontinuity design. Econometrica , 69, 201–209.CrossRefGoogle Scholar
Imbens, G. W., & Lemieux, T. (2008). Regression discontinuity designs: A guide to practice. Journal of Econometrics , 142, 615–635.CrossRefGoogle Scholar
Kreiß, A., & Rothe, C. (2023). Inference in regression discontinuity designs with high-dimensional covariates. Econometrics Journal , 26, 105–123.CrossRefGoogle Scholar
Lei, L., & Ding, P. (2021). Regression adjustment in completely randomized experiments with a diverging number of covariates. Biometrika , 108, 815–828.CrossRefGoogle Scholar
Lin, W. (2013). Agnostic notes on regression adjustments to experimental data: Reexamining Freedman’s critique. Annals of Applied Statistics , 7, 295–318.CrossRefGoogle Scholar
Ludwig, J., & Miller, D. L. (2007). Does head start improve children’s life chances? Evidence from a regression discontinuity design. Quarterly Journal of Economics , 122, 159–208.CrossRefGoogle Scholar
Ruppert, D., & Wand, M. P. (1994). Multivariate locally weighted least squares regression. Annals of Statistics , 22, 1346–1370.CrossRefGoogle Scholar
van de Geer, S., Bühlmann, P., Ritov, Y., & Dezeure, R. (2014). On asymptotically optimal confidence regions and tests for high-dimensional models. Annals of Statistics , 42, 1166–1202.CrossRefGoogle Scholar
van der Vaart, A. W., & Wellner, J. A. (1996). Weak convergence and empirical processes . Springer.CrossRefGoogle Scholar
Zhang, C.-H., & Zhang, S. S. (2014). Confidence intervals for low dimensional parameters in high dimensional linear models. Journal of the Royal Statistical Society, B , 76, 217–242.CrossRefGoogle Scholar