Article contents
ON THE CONVERGENCE RATE OF POTENTIALS OF BRENIER MAPS
Published online by Cambridge University Press: 15 February 2021
Abstract
The theory of optimal transportation has experienced a sharp increase in interest in many areas of economic research such as optimal matching theory and econometric identification. A particularly valuable tool, due to its convenient representation as the gradient of a convex function, has been the Brenier map: the matching obtained as the optimizer of the Monge–Kantorovich optimal transportation problem with the euclidean distance as the cost function. Despite its popularity, the statistical properties of the Brenier map have yet to be fully established, which impedes its practical use for estimation and inference. This article takes a first step in this direction by deriving a convergence rate for the simple plug-in estimator of the potential of the Brenier map via the semi-dual Monge–Kantorovich problem. Relying on classical results for the convergence of smoothed empirical processes, it is shown that this plug-in estimator converges in standard deviation to its population counterpart under the minimax rate of convergence of kernel density estimators if one of the probability measures satisfies the Poincaré inequality. Under a normalization of the potential, the result extends to convergence in the 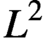 $L^2$ norm, while the Poincaré inequality is automatically satisfied. The main mathematical contribution of this article is an analysis of the second variation of the semi-dual Monge–Kantorovich problem, which is of independent interest.
$L^2$ norm, while the Poincaré inequality is automatically satisfied. The main mathematical contribution of this article is an analysis of the second variation of the semi-dual Monge–Kantorovich problem, which is of independent interest.
- Type
- MISCELLANEA
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
I would like to thank the Editor Peter Phillips, the Co-Editor Ivan Fernandez-Val, and especially two referees for their effort and important comments which helped me improve the paper substantially. I would also like to thank Susanne Schennach for helpful feedback. I wrote the initial version of this paper while a graduate student in the Economics Department at Brown University. All errors are mine.
References
REFERENCES
- 3
- Cited by


