Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T21:04:11.549Z Has data issue: false hasContentIssue false
  • English
  • Français

ON PLUG-IN ESTIMATION OF LONG MEMORY MODELS

Published online by Cambridge University Press:  31 March 2005

Offer Lieberman
Offer Lieberman
Affiliation:
Technion—Israel Institute of Technology
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the Gaussian ARFIMA(j,d,l) model, with spectral density 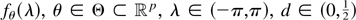and an unknown mean 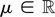. For this class of models, the n−1-normalized information matrix of the full parameter vector, (μ,θ), is asymptotically degenerate. To estimate θ, Dahlhaus (1989, Annals of Statistics 17, 1749–1766) suggested using the maximizer of the plug-in log-likelihood, 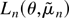, where 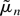is any n(1−2d)/2-consistent estimator of μ. The resulting estimator is a plug-in maximum likelihood estimator (PMLE). This estimator is asymptotically normal, efficient, and consistent, but in finite samples it has some serious drawbacks. Primarily, none of the Bartlett identities associated with 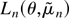are satisfied for fixed n. Cheung and Diebold (1994, Journal of Econometrics 62, 301–316) conducted a Monte Carlo simulation study and reported that the bias of the PMLE is about 3–4 times the bias of the regular maximum likelihood estimator (MLE). In this paper, we derive asymptotic expansions for the PMLE and show that its second-order bias is contaminated by an additional term, which does not exist in regular cases. This term arises because of the failure of the first Bartlett identity to hold and seems to explain Cheung and Diebold's simulated results. We derive similar expansions for the Whittle MLE, which is another estimator tacitly using the plug-in principle. An application to the ARFIMA(0,d,0) shows that the additional bias terms are considerable.Research on this topic commenced during 2000–2002, while the author was visiting the Cowles Foundation for Research in Economics at Yale University. The author is most grateful to the Cowles Foundation for their generous hospitality and to Donald Andrews and Peter Phillips for numerous helpful comments.

Type
Research Article
Information
Econometric Theory , Volume 21 , Issue 2 , April 2005 , pp. 431 - 454
Copyright
© 2005 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adenstedt, R.K. (1974) On large-sample estimation for the mean of a stationary random sequence. Annals of Statistics 2, 1095–1107.Google Scholar
Andrews, D.W.K. & O. Lieberman (2005) Valid Edgeworth expansions for the Whittle maximum likelihood estimator for stationary long-memory Gaussian time series. Econometric Theory (forthcoming).Google Scholar
Andrews, D.W.K., O. Lieberman, & V. Marmer (2005) Higher-order improvement of the parametric bootstrap for long-memory Gaussian processes. Journal of Econometrics (forthcoming).Google Scholar
Cheung, Y.W. & F.X. Diebold (1994) On maximum likelihood estimation of the differencing parameter of fractionally integrated noise with unknown mean. Journal of Econometrics 62, 301–316.Google Scholar
Cox, D.R. & E.J. Snell (1968) A general definition of residuals (with discussion). Journal of the Royal Statistical Society, Series B 30, 248–275.Google Scholar
Dahlhaus, R. (1989) Efficient parameter estimation for self-similar processes. Annals of Statistics 17, 1749–1766.Google Scholar
Fox, R. & M.S. Taqqu (1986) Large sample properties of parameter estimates for strongly dependent stationary Gaussian time series. Annals of Statistics 14, 517–532.Google Scholar
Hurst, H.E. (1951) Long-term storage capacity of reservoirs. Transactions of the American Society of Civil Engineers 116, 770–808.Google Scholar
Lawley, D.N. (1956) A general method for approximating to the distribution of likelihood ratio criteria. Biometrika 43, 295–303.Google Scholar
Lieberman, O. (2001) Penalised maximum likelihood estimation for fractional Gaussian processes. Biometrika 88, 888–894.Google Scholar
Lieberman, O. & P.C.B. Phillips (2004a) Expansions for the distribution of the maximum likelihood estimator of the fractional difference parameter. Econometric Theory 20, 464–484.Google Scholar
Lieberman, O. & P.C.B. Phillips (2004b) Error bounds and asymptotic expansions for Toeplitz product functionals of unbounded spectra. Journal of Time Series Analysis 25, 733–753.Google Scholar
Lieberman, O., J. Rousseau, & D.M. Zucker (2000) Small-sample likelihood-based inference in the ARFIMA model. Econometric Theory 16, 231–248.Google Scholar
Lieberman, O., J. Rousseau, & D.M. Zucker (2001) Valid Edgeworth expansions for the sample autocorrelation function under long range dependence. Econometric Theory 17, 257–275.Google Scholar
Lieberman, O., J. Rousseau, & D.M. Zucker (2003) Valid Edgeworth expansions for the maximum likelihood estimator of the parameter of a stationary, Gaussian, strongly dependent process. Annals of Statistics 31, 586–612.Google Scholar
McCullagh, P. (1987) Tensor Methods in Statistics. Chapman and Hall.
Taniguchi, M. (1991) Higher Order Asymptotic Theory for Time Series Analysis. Springer-Verlag.