Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-12T11:05:16.201Z Has data issue: false hasContentIssue false
  • English
  • Français

On Asymptotics of the Sample Distribution for a Class of Linear Process Models in Economics

Published online by Cambridge University Press:  18 October 2010

C. H. Hesse
C. H. Hesse
Affiliation:
University of California at Berkeley
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 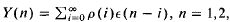… be a moving average process of infinite order where the innovations ε(k) are in the domain of attraction of a stable law with index α ε (0, 2) and the parameter sequence decreases at a polynomial or exponential rate. These and similar processes have recently received increased attention both in the econometrics and statistics/probability literature. The present paper studies almost sure uniform rates of convergence of the empirical distribution function. Applications of these infinite variance processesin econometrics are mentioned.

Type
Articles
Information
Econometric Theory , Volume 8 , Issue 3 , September 1992 , pp. 330 - 342
Copyright
Copyright © Cambridge University Press 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Akgiray, V. & Booth, G.G.. The stable-law model of stock returns. Journal of Business and Economic Statistics 6 (1988): 51–57.Google Scholar
2. Avram, F. & Taqqu, M.S.. Weak convergence of moving averages with infinite variance. In Eberlein, E. and Taqqu, M.S. (eds.), Dependence in Probability and Statistics: A Survey of Recent Results. Boston: Birkhäuser, 1986.Google Scholar
3.Avram, F. & Taqqu, M.S.. Weak convergence of sums of moving averages in the ce-stable domain of attraction, mimeo, Boston University, 1989.Google Scholar
4. Bingham, N.H, Goldie, CM. & Teugels, J.L.. Regular Variation. Encyclopedia of Mathematics and its Applications, Cambridge University Press, 1987.Google Scholar
5.Blattberg, R.C. & Gonedes, N.J.. A comparison of the stable and Student distributions as statistical models for stock prices. Journal of Business 47 (1974): 244–280.CrossRefGoogle Scholar
6.Brockwell, P.J. & Davis, R.A.. Time Series: Theory and Methods. New York: Springer Verlag, 1987.CrossRefGoogle Scholar
7.Chan, N.H. & Tran, L.T.. On the first order autoregressive process with infinite variance. Econometric Theory 5 (1989): 354–362.CrossRefGoogle Scholar
8.Davis, R.A. & Resnick, S.I.. Limit theory for moving averages of random variables with regularly varying tail probabilities. Annals of Probability 13 (1985): 179–195.CrossRefGoogle Scholar
9.Davis, R.A. & Resnick, S.I.. Limit theory for the sample covariance and correlation functions of moving averages. Annals of Statistics 14 (1986): 533–558.Google Scholar
10.Davis, R.A. & Resnick, S.I.. More limit theory for sample correlation functions of moving averages. Stochastic Processes and their Applications 20 (1985): 257–279.CrossRefGoogle Scholar
11.Durbin, J. Distribution Theory for Tests Based on the Sample Distribution Function. Regional Conference Series in Applied Mathematics, Vol. 9 SIAM, Philadelphia, 1973.CrossRefGoogle Scholar
12.Fielitz, B.D. & Rozelle, J.P.. Stable distributions and mixtures of distributions hypotheses for common stock returns. Journal of the American Statistical Association 78 (1982): 28–36.Google Scholar
13.Granger, C.W.J. & Orr, D.. Infinite variance and research strategy in time series analysis. Journal of the American Statistical Association 67 (1972): 275–285.Google Scholar
14. Györfi, L., Hardle, W., Sarda, P., & Vieu, P.. Nonparametric Curve Estimation from Time Series. Lecture Notes in Statistics, Springer Verlag, 1989.Google Scholar
15.Hall, J.A, Brorsen, B.W. & Irwin, S.H.. The distribution of futures prices: A test of the stable-Paretian and mixtures of normal hypothesis. Journal of Financial and Quantitative Analysis 24(1989): 105–116.Google Scholar
16.Hannan, E.J. & Hesse, C.H.. Rates of convergence for the quantile function of a linear process. Australian Journal of Statistics 304 (1987): 283–295.Google Scholar
17.Hesse, C.H. Rates of convergence for the empirical distribution function and the empirical characteristic function of a broad class of linear processes. Journal of Multivariate Analysis 35 (1990): 186–202.CrossRefGoogle Scholar
18.Ibragimov, LA. Some limit theorems for stationary processes. Theory of Probability and its Applications 1 (1962): 349–382.Google Scholar
19.Kolmogorov, A.N. & Rozanov, Y.A.. On strong mixing conditions for stationary Gaussian processes. Theory of Probability and its Applications 5 (1960): 204–207.CrossRefGoogle Scholar
20.Mandelbrot, B. The variation of certain speculative prices. Journal of Business 36 (1963): 394–419.CrossRefGoogle Scholar
21.Pham, T.D. & Tran, L.T.. Some mixing properties of time series models. Stochastic Processes and Their Applications 19 (1986): 297–303.CrossRefGoogle Scholar
22.Phillips, P.C.B. Time series regression with a unit root and infinite-variance errors. Econometric Theory 6 (1990): 44–62.CrossRefGoogle Scholar
23.Phillips, P.C.B. & Loretan, M.. Testing covariance stationarity under moment condition failure with application to common stock returns. Cowles Foundation Discussion paper No. 947, Yale University, 1990.Google Scholar
24.Phillips, P.C.B. & Solo, V.. Asymptotics for linear processes. Cowles Foundation Discussion Paper No. 932, Yale University, 1989.Google Scholar
25.Rosenblatt, M. Acentral limit theorem and strong mixing condition. Proceedings of the National Academy of Sciences 42 (1956): 43–47.Google Scholar
26.Samuelson, P.A. Limited liability, shortselling, bounded utility, and infinite-variance stable distributions. Journal of Financial and Quantitative Analysis 11 (1975): 485–503.CrossRefGoogle Scholar
27.Sarda, P. & Vieu, P.. Empirical distribution function for mixing random variables: Application in nonparametric hazard estimation. Statistics 20 (1989): 559–571.CrossRefGoogle Scholar
28.Shorack, G.R. & Wellner, J.A.. Empirical Processes with Applications to Statistics. New York: Wiley, 1986.Google Scholar
29.Smirnov, N. V. Approximate laws of distribution of random variables from empirical data. UspehkiMat. Nauk. 10(1944): 179–206.Google Scholar
30.So, J. The sub-Gaussian distribution of currency futures: stable Paretian or nonstationary? Review of Economics and Statistics 69 (1987): 100–107.Google Scholar
31.Withers, C.S. Conditions for linear processes to be strong mixing. Theory of Probability and Related Fields 57 (1981): 481–494.Google Scholar