Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T07:29:54.407Z Has data issue: false hasContentIssue false
  • English
  • Français

NONPARAMETRIC SIGNIFICANCE TESTING IN MEASUREMENT ERROR MODELS

Published online by Cambridge University Press:  04 June 2021

Hao Dong  and
Luke Taylor
Hao Dong
Affiliation:
Southern Methodist University
Luke Taylor*
Affiliation:
Aarhus University
*
Address correspondence to Luke Taylor, Department of Economics and Business Economics, Aarhus University, Fuglesangs Allé 4, 8210Aarhus, Denmark; e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop the first nonparametric significance test for regression models with classical measurement error in the regressors. In particular, a Cramér-von Mises test and a Kolmogorov–Smirnov test for the null hypothesis 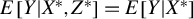$E\left [Y|X^{*},Z^{*}\right ]=E\left [Y|X^{*}\right ]$ are proposed when only noisy measurements of 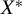$X^{*}$ and $Z^{*}$ are available. The asymptotic null distributions of the test statistics are derived, and a bootstrap method is implemented to obtain the critical values. Despite the test statistics being constructed using deconvolution estimators, we show that the test can detect a sequence of local alternatives converging to the null at the 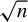$\sqrt {n}$ -rate. We also highlight the finite sample performance of the test through a Monte Carlo study.

Type
ARTICLES
Information
Econometric Theory , Volume 38 , Issue 3 , June 2022 , pp. 454 - 496
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors would like to thank the Editor, Associate Editor, three anonymous referees, Karun Adusumilli, Taisuke Otsu, Ricardo Reis, and Peter Robinson for helpful comments. Financial support from the SMU Dedman College Research Fund (12-412268; Dong), and the Aarhus University Research Fund (AUFF-26852; Taylor) is gratefully acknowledged.

References

REFERENCES

Adusumilli, K., Kurisu, D., Otsu, T. & Whang, Y. J. (2020) Inference on distribution functions under measurement error. Journal of Econometrics 215(1), 131–164.CrossRefGoogle Scholar
Ahn, H. & Powell, J. L. (1993) Semiparametric estimation of censored selection models with a nonparametric selection mechanism. Journal of Econometrics 58(1–2), 3–29.CrossRefGoogle Scholar
Bierens, H. J. (1982) Consistent model specification tests. Journal of Econometrics 20(1), 105–134.CrossRefGoogle Scholar
Bierens, H. J. (1990) A consistent conditional moment test of functional form. Econometrica 58(6), 1443–1458.CrossRefGoogle Scholar
Bierens, H. J. & Ploberger, W. (1997) Asymptotic theory of integrated conditional moment tests. Econometrica 65(5), 1129–1151.CrossRefGoogle Scholar
Bissantz, N., Dümbgen, L., Holzmann, H. & Munk, A. (2007) Non-parametric confidence bands in deconvolution density estimation. Journal of the Royal Statistical Society: Series B 69(3), 483–506.CrossRefGoogle Scholar
Butucea, C. & Taupin, M. L. (2008) New M-estimators in semi-parametric regression with errors in variables. Annales de l’IHP Probabilités et Statistiques 44(3), 393–421.Google Scholar
Carroll, R. J. & Hall, P. (1988) Optimal rates of convergence for deconvolving a density. Journal of the American Statistical Association 83(404), 1184–1186.CrossRefGoogle Scholar
Chen, X. & Fan, Y. (1999) Consistent hypothesis testing in semiparametric and nonparametric models for econometric time series. Journal of Econometrics 91(2), 373–401.CrossRefGoogle Scholar
Chen, X. & White, H. (1998) Central limit and functional central limit theorems for Hilbert-valued dependent heterogeneous arrays with applications. Econometric Theory 14(2), 260–284.CrossRefGoogle Scholar
Chernozhukov, V., Chetverikov, D. & Kato, K. (2014) Gaussian approximation of suprema of empirical processes. Annals of Statistics 42(4), 1564–1597.CrossRefGoogle Scholar
Chernozhukov, V., Chetverikov, D. & Kato, K. (2015) Comparison and anti-concentration bounds for maxima of Gaussian random vectors. Probability Theory and Related Fields 162(1–2), 47–70.CrossRefGoogle Scholar
Chernozhukov, V., Chetverikov, D. & Kato, K. (2016) Empirical and multiplier bootstraps for suprema of empirical processes of increasing complexity, and related Gaussian couplings. Stochastic Processes and Their Applications 126(12), 3632–3651.CrossRefGoogle Scholar
Delaigle, A. & Hall, P. (2016) Methodology for non-parametric deconvolution when the error distribution is unknown. Journal of the Royal Statistical Society: Series B 78(1), 231–252.CrossRefGoogle Scholar
Delaigle, A., Hall, P. & Jamshidi, F. (2015) Confidence bands in non-parametric errors-in-variables regression. Journal of the Royal Statistical Society: Series B 77(1), 149–169.CrossRefGoogle Scholar
Delaigle, A., Hall, P. & Meister, A. (2008) On deconvolution with repeated measurements. Annals of Statistics 36(2), 665–685.CrossRefGoogle Scholar
Delaigle, A., & Gijbels, I. (2004) Bootstrap bandwidth selection in kernel density estimation from a contaminated sample. Annals of the Institute of Statistical Mathematics, 56(1), 19–47.CrossRefGoogle Scholar
Delaigle, A., & Meister, A. (2007) Nonparametric regression estimation in the heteroscedastic errors-in-variables problem. Journal of the American Statistical Association, 102(480), 1416–1426.CrossRefGoogle Scholar
Delgado, M. A. & González-Manteiga, W. (2001) Significance testing in nonparametric regression based on the bootstrap. Annals of Statistics 29, 1469–1507.CrossRefGoogle Scholar
Dong, H., Otsu, T., & Taylor, L. (2020) Average derivative estimation under measurement error. Econometric Theory, first published online 13 November 2020. https://doi.org/10.1017/S0266466620000432. Google Scholar
Dudley, R. M. (2002) Real Analysis and Probability. Cambridge University Press.CrossRefGoogle Scholar
Fan, J. & Truong, Y. K. (1993) Nonparametric regression with errors in variables. Annals of Statistics 21(4), 1900–1925.CrossRefGoogle Scholar
Fan, Y. (1995) Average derivative estimation with errors-in-variables. Journal of Nonparametric Statistics 4(4), 395–407.CrossRefGoogle Scholar
Fan, Y., & Li, Q. (2000) Consistent model specification tests: Kernel-based tests versus Bierens’ ICM tests. Econometric Theory, 1016–1041.CrossRefGoogle Scholar
Fisher, R. A. (1929) The statistical method in psychical research. Proceedings of the Society for Psychical Research 39, 189–192.Google Scholar
Giné, E. & Nickl, R. (2016) Mathematical Foundations of Infinite-Dimensional Statistical Models. Cambridge University Press.CrossRefGoogle Scholar
González-Manteiga, W. & Crujeiras, R. M. (2013) An updated review of goodness-of-fit tests for regression models. Test 22(3), 361–411.CrossRefGoogle Scholar
Hall, P. & Ma, Y. (2007a) Semiparametric estimators of functional measurement error models with unknown error. Journal of the Royal Statistical Society: Series B 69(3), 429–446.CrossRefGoogle Scholar
Hall, P. & Ma, Y. (2007b) Testing the suitability of polynomial models in errors-in-variables problems. Annals of Statistics 35(6), 2620–2638.CrossRefGoogle Scholar
Hall, P. & Meister, A. (2007) A ridge-parameter approach to deconvolution. Annals of Statistics 35(4), 1535–1558.CrossRefGoogle Scholar
Härdle, W. & Mammen, E. (1993) Comparing nonparametric versus parametric regression fits. Annals of Statistics 21(4), 1926–1947.CrossRefGoogle Scholar
Hu, Y. & Ridder, G. (2012) Estimation of nonlinear models with mismeasured regressors using marginal information. Journal of Applied Econometrics 27(3), 347–385.CrossRefGoogle Scholar
Kato, K. & Sasaki, Y. (2018) Uniform confidence bands in deconvolution with unknown error distribution. Journal of Econometrics 207(1), 129–161.CrossRefGoogle Scholar
Kato, K. & Sasaki, Y. (2019) Uniform confidence bands for nonparametric errors-in-variables regression. Journal of Econometrics 213(2), 516–555.CrossRefGoogle Scholar
Kotlarski, I. (1967) On characterizing the gamma and the normal distribution. Pacific Journal of Mathematics 20(1), 69–76.CrossRefGoogle Scholar
Kurisu, D. & Otsu, T. (2021) On uniform convergence of deconvolution estimator from repeated measurements. Econometric Theory, first published online 25 January 2021. https://doi.org/10.1017/S0266466620000572.Google Scholar
Lavergne, P. & Vuong, Q. H. (2000) Nonparametric significance testing. Econometric Theory 16(4), 576–601.CrossRefGoogle Scholar
Li, T. & Vuong, Q. H. (1998) Nonparametric estimation of the measurement error model using multiple indicators. Journal of Multivariate Analysis 65(2), 139–165.CrossRefGoogle Scholar
Ma, Y. & Li, R. (2010) Variable selection in measurement error models. Bernoulli 16(1), 274–300.CrossRefGoogle ScholarPubMed
McMurry, T. L. & Politis, D. N. (2004) Nonparametric regression with infinite order flat-top kernels. Journal of Nonparametric Statistics 16, 549–562.CrossRefGoogle Scholar
Meister, A. (2009) Deconvolution Problems in Nonparametric Statistics. Springer.CrossRefGoogle Scholar
Otsu, T. & Taylor, L. (2020) Specification testing for errors-in-variables models. Econometric Theory, first published online 19 June 2020. https://doi.org/10.1017/S0266466620000262.Google Scholar
Powell, J. L., Stock, J. H. & Stoker, T. M. (1989) Semiparametric estimation of index coefficients. Econometrica 57(6), 1403–1430.CrossRefGoogle Scholar
Robinson, P. M. (1989) Hypothesis testing in semiparametric and nonparametric models for econometric time series. The Review of Economic Studies 56(4), 511–534.CrossRefGoogle Scholar
Schennach, S. M. (2004) Estimation of nonlinear models with measurement error. Econometrica 72(1), 33–75.CrossRefGoogle Scholar
Schennach, S. M. (2016) Recent advances in the measurement error literature. Annual Review of Economics 8, 341–377.CrossRefGoogle Scholar
Stefanski, L. A. & Carroll, R. J. (1990) Deconvolving kernel density estimators. Statistics 21(2), 169–184.CrossRefGoogle Scholar
Stinchcombe, M. B. & White, H. (1998) Consistent specification testing with nuisance parameters present only under the alternative. Econometric Theory 14(3), 295–325.CrossRefGoogle Scholar
Stute, W. (1997) Nonparametric model checks for regression. Annals of Statistics 25(2), 613–641.CrossRefGoogle Scholar
Su, L. & White, H. (2008) A nonparametric Hellinger metric test for conditional independence. Econometric Theory 24(4), 829–864.CrossRefGoogle Scholar
Van Der Vaart, A. W. & Wellner, J. A. (1996) Weak Convergence and Empirical Processes. Springer.CrossRefGoogle Scholar
Van Es, A. J. & Uh, H. W. (2005) Asymptotic normality for kernel type deconvolution estimators. Scandinavian Journal of Statistics 32, 467–483.Google Scholar
Zhang, X., Wang, H., Ma, Y. & Carroll, R. J. (2017) Linear model selection when covariates contain errors. Journal of the American Statistical Association 112(520), 1553–1561.CrossRefGoogle ScholarPubMed
Zhu, L. & Cui, H. (2003) A semi-parametric regression model with errors in variables. Scandinavian Journal of Statistics 30(2), 429–442.CrossRefGoogle Scholar