Hostname: page-component-6bf8c574d5-h6jzd Total loading time: 0.001 Render date: 2025-02-22T22:17:43.588Z Has data issue: false hasContentIssue false
  • English
  • Français

LEAST TRIMMED SQUARES: NUISANCE PARAMETER FREE ASYMPTOTICS

Published online by Cambridge University Press:  17 February 2025

Vanessa Berenguer-Rico Open the ORCID record for Vanessa Berenguer-Rico [Opens in a new window]  and
Bent Nielsen Open the ORCID record for Bent Nielsen [Opens in a new window]
Vanessa Berenguer-Rico*
Affiliation:
University of Oxford
Bent Nielsen
Affiliation:
University of Oxford
*
Address correspondence to Vanessa Berenguer-Rico, Mansfield College & Department of Economics, University of Oxford, Oxford, UK, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Least Trimmed Squares (LTS) regression estimator is known to be very robust to the presence of “outliers”. It is based on a clear and intuitive idea: in a sample of size n, it searches for the h-subsample of observations with the smallest sum of squared residuals. The remaining 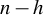$n-h$ observations are declared “outliers”. Fast algorithms for its computation exist. Nevertheless, the existing asymptotic theory for LTS, based on the traditional 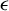$\epsilon $-contamination model, shows that the asymptotic behavior of both regression and scale estimators depend on nuisance parameters. Using a recently proposed new model, in which the LTS estimator is maximum likelihood, we show that the asymptotic behavior of both the LTS regression and scale estimators are free of nuisance parameters. Thus, with the new model as a benchmark, standard inference procedures apply while allowing a broad range of contamination.

Type
ARTICLES
Information
Econometric Theory , First View , pp. 1 - 39
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Footnotes

Comments from P. Guggenberger and the referees are gratefully acknowledged.

References

REFERENCES

Agullo, J., Croux, C., & Van Aelst, S. (2008). The multivariate least-trimmed squares estimator. Journal of Multivariate Analysis , 99, 311–338.CrossRefGoogle Scholar
Alfons, A., Croux, C., & Gelper, S. (2013). Sparse least trimmed squares regression for analyzing high-dimensional large data sets. Annals of Applied Statistics , 7, 226–248.CrossRefGoogle Scholar
Atkinson, A. C., Riani, M., & Cerioli, A. (2010). The forward search: Theory and data analysis (with discussion). Journal of the Korean Statistical Society , 39, 117–163.CrossRefGoogle Scholar
Bednarski, T., & Clarke, B. R. (1993). Trimmed likelihood estimation of location and scale of the normal distribution. Australian Journal of Statistics , 35, 141–153.CrossRefGoogle Scholar
Berenguer-Rico, V., Johansen, S., & Nielsen, B. (2023). A model where the least trimmed squares estimator is maximum likelihood. Journal of the Royal Statistical Society. Series B , 85, 886–912.CrossRefGoogle Scholar
Berenguer-Rico, V. & Nielsen, B. (2023). Normality testing after outlier removal. Econometrics and Statistics .CrossRefGoogle Scholar
Butler, R. (1982). Nonparametric interval and point prediction using data trimmed by a Grubbs-type outlier rule. Annals of Statistics , 10, 197–204.CrossRefGoogle Scholar
Chen, X. R., & Wu, Y. H. (1988). Strong consistency of M-estimators in linear models. Journal of Multivariate Analysis , 27, 116–130.CrossRefGoogle Scholar
Chibisov, D. M. (1964). On limit distributions for order statistics. Theory of Probability and Its Applications , 9, 142–147.CrossRefGoogle Scholar
Čížek, P. (2005). Least trimmed squares in nonlinear regression under dependence. Journal of Statistical Planning and Inference , 136, 3967–3988.CrossRefGoogle Scholar
Clarke, B. R. (2018). Robustness theory and application . John Wiley & Sons.CrossRefGoogle Scholar
Croux, C. & Rousseeuw, P. J. (1992). A class of high-breakdown scale estimators based on subranges. Communications in Statistics. Theory and Methods , 21, 1935–1951.CrossRefGoogle Scholar
DasGupta, A. (2008). Asymptotic theory of statistics and probability . Springer.Google Scholar
Davies, L. (1990). The asymptotics of S-estimators in the linear regression model. Annals of Statistics , 18, 1651–1675.CrossRefGoogle Scholar
Galambos, J. (1978). The asymptotic theory of extreme order statistics . John Wiley & Sons.Google Scholar
Gallegos, M. T. & Ritter, G. (2009). Trimmed ML estimation of contaminated mixtures. Sankhya A , 71, 164–220.Google Scholar
Gradshteyn, I. S., & Ryzhik, I. M. (1965). Table of integrals, series and products (4th ed.). Academic Press.Google Scholar
Gumbel, E. J., & Keeney, R. D. (1950). The extremal quotient. Annals of Mathematical Statistics , 21, 523–538.CrossRefGoogle Scholar
He, X., Jurečková, J., Koenker, R., & Portnoy, S. (1990). Tail behavior of regression estimators and their breakdown points. Econometrica , 58, 1195–1214.CrossRefGoogle Scholar
Hössjer, O. (1994). Rank-based estimates in the linear model with high breakdown point. Journal of the American Statistical Association , 89, 149–158.Google Scholar
Huber, P. J. (1964). Robust estimation of a location parameter. Annals of Mathematical Statistics , 35, 73–101.CrossRefGoogle Scholar
Johansen, S. (1995). Likelihood based inference on cointegration in the vector autoregressive model . Oxford University Press.CrossRefGoogle Scholar
Johansen, S., & Nielsen, B. (2009). Saturation by indicators in regression models. In Castle, J. L. & Shephard, N. (Eds.), The methodology and practice of econometrics: Festschrift in honour of David F (pp. 1–36). Oxford University Press.Google Scholar
Johansen, S., & Nielsen, B. (2016). Asymptotic theory of outlier detection algorithms for linear time series regression models (with discussion). Scandinavian Journal of Statistics , 43, 321–381.CrossRefGoogle Scholar
Johansen, S. & Nielsen, B. (2019). Boundedness of M-estimators for multiple linear regression in time series. Econometric Theory , 35, 653–683.CrossRefGoogle Scholar
Karamata, J. (1930). Sur une mode de croissance régulière des fonctions. Mathematica (Cluj) , 4, 38–53.Google Scholar
Leadbetter, M. R., Lindgren, G., & Rootzén, H. (1982). Extremes and related properties of random sequences and processes . Springer.Google Scholar
Raymaekers, J. & Rousseeuw, P. J. (2024). The cellwise minimum covariance determinant estimator. Journal of the American Statistical Association , 119, 2610–2621.CrossRefGoogle Scholar
Rousseeuw, P. J. (1984). Least median of squares regressions. Journal of the American Statistical Association , 79, 871–880.CrossRefGoogle Scholar
Rousseeuw, P. (1985). Multivariate estimation with high breakdown point. In Grossmann, W., Pflug, G., Vincze, I., & Wertz, W. (Eds.), Mathematical statistics and applications (pp. 283–297). Reidel.CrossRefGoogle Scholar
Rousseeuw, P. J. (1994). Unconventional features of positive-breakdown estimators. Statistics & Probability Letters , 19, 417–431.CrossRefGoogle Scholar
Rousseeuw, P. J. & Hubert, M. (1997). Recent developments in PROGRESS. In Dodge, Y. (Ed.), L 1-statistical procedures and related topics, vol 31 of Lecture Notes–Monograph Series (pp. 201–214). Institute of Mathematical Statistics.CrossRefGoogle Scholar
Rousseeuw, P. J. & Leroy, A. M. (1987). Robust regression and outlier detection . John Wiley & Sons.CrossRefGoogle Scholar
Rousseeuw, P. J., Perrotta, D., Riani, M., & Hubert, M. (2019). Robust monitoring of time series with application to fraud detection. Econometrics and Statistics , 9, 108–121.CrossRefGoogle Scholar
Rousseeuw, P. J., & van Driessen, K. (2000). An algorithm for positive-breakdown regression based on concentration steps In Gaul, W., Opitz, O., & Schader, M. (Eds.), Data analysis: Scientific modeling and practical application (pp. 335–346). Springer Verlag.CrossRefGoogle Scholar
Scholz, F. W. (1980). Towards a unified definition of maximum likelihood. Canadian Journal of Statistics , 8, 193–203.CrossRefGoogle Scholar
Soms, A. P. (1976). An asymptotic expansion for the tail area of the t-distribution. Journal of the American Statistical Association , 71, 728–730.Google Scholar
Vandev, D. L., & Neykov, N. M. (1993). Robust maximum likelihood in the Gaussian case. In Morgenthaler, S., Ronchetti, E., & Stahel, W. A. (Eds.), New directions in data analysis and robustness (pp. 259–264). Birkhäuser.Google Scholar
Víšek, J. Á. (2006). The least trimmed squares; part III: Asymptotic normality. Kybernetika , 42, 203–224.Google Scholar
Watts, V., Rootzén, H., & Leadbetter, M. R. (1982). On limiting distributions of intermediate order statistics from stationary sequences. Annals of Probability , 10, 653–662.CrossRefGoogle Scholar
Wilms, I., & Croux, C. (2016). Robust sparse canonical correlation analysis. BMC Systems Biology , 10, Article 72, 13 pp.CrossRefGoogle ScholarPubMed