Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T07:31:06.347Z Has data issue: false hasContentIssue false
  • English
  • Français

LEAST SQUARES AND IVX LIMIT THEORY IN SYSTEMS OF PREDICTIVE REGRESSIONS WITH GARCH INNOVATIONS

Published online by Cambridge University Press:  23 March 2021

Tassos Magdalinos
Tassos Magdalinos*
Affiliation:
University of Southampton
*
Address correspondence to Tassos Magdalinos, University of Southampton, Southampton, UK; e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper examines the effect of conditional heteroskedasticity on least squares inference in stochastic regression models of unknown integration order and proposes an inference procedure that is robust to models within the (near) I(0)–(near) I(1) range with GARCH innovations. We show that a regressor signal of exact order 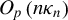$O_{p}\left ( n\kappa _{n}\right ) $ for arbitrary $\,\kappa _{n}\rightarrow \infty $ is sufficient to eliminate stationary GARCH effects from the limit distributions of least squares based estimators and self-normalized test statistics. 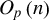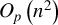The above order dominates the $O_{p}\left ( n\right ) $ signal of stationary regressors but may be dominated by the $O_{p}\left ( n^{2}\right ) $ signal of I(1) regressors, thereby showing that least squares invariance to GARCH effects is not an exclusively I(1) phenomenon but extends to processes with persistence degree arbitrarily close to stationarity. The theory validates standard inference for self normalized test statistics based on the ordinary least squares estimator when $\kappa _{n}\rightarrow \infty $ and 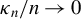$\kappa _{n}/n\rightarrow 0$ and the IVX estimator (Phillips and Magdalinos (2009a), Econometric Inference in the Vicinity of Unity. Working paper, Singapore Management University; Kostakis, Magdalinos, and Stamatogiannis, 2015a, Review of Financial Studies 28(5), 1506–1553.) when $\kappa _{n}\rightarrow \infty $ and the innovation sequence of the system is a covariance stationary vec-GARCH process. An adjusted version of the IVX–Wald test is shown to also accommodate GARCH effects in purely stationary regressors, thereby extending the procedure’s validity over the entire (near) I(0)–(near) I(1) range of regressors under conditional heteroskedasticity in the innovations. It is hoped that the wide range of applicability of this adjusted IVX–Wald test, established in Theorem 4.4, presents an advantage for the procedure’s suitability as a tool for applied research.

Type
ARTICLES
Information
Econometric Theory , Volume 38 , Issue 5: YALE 2018 CONFERENCE IN HONOR OF PETER C. B. PHILLIPS: PART I , October 2022 , pp. 875 - 912
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This paper is dedicated to Peter Phillips with gratitude for his mentorship, friendship and generosity over the years.

I would like to thank Don Andrews, Stelios Arvanitis, Ioannis Kasparis, Katerina Petrova, and two anonymous referees for valuable suggestions and comments. Financial support by the British Academy is gratefully acknowledged.

References

REFERENCES

Abadir, K.M. & Magnus, J.R. (2005) Matrix Algebra. Econometric Exercises, vol.1. Cambridge University Press.CrossRefGoogle Scholar
Andrews, D.W.K. & Guggenberger, P. (2008) Asymptotics for stationary very nearly unit root processes. Journal of Time Series Analysis 29(1), 203–212.Google Scholar
Andrews, D.W.K. & Guggenberger, P. (2012) Asymptotics for LS, GLS, and feasible GLS statistics in an AR(1) model with conditional heteroskedasticity. Journal of Econometrics 169(2), 196–210.CrossRefGoogle Scholar
Andrews, D.W.K. & Guggenberger, P. (2014) A conditional-heteroskedasticity-robust confidence interval for the autoregressive parameter. Review of Economics and Statistics 96(2), 376–381.CrossRefGoogle Scholar
Bollersev, T. (1986) Generalized autoregressive conditional heteroscedasticity. Journal of Econometrics 31, 307–327.CrossRefGoogle Scholar
Boussama, F. (2006) Ergodicité des chaînes de Markov à valeurs dans une variété algébrique: application aux modèles GARCH multivariés. Comptes Rendus de l’ Academie des Sciences Paris 343, 275–278.Google Scholar
Boussama, F., Fuchs, F., & Stelzer, R. (2011) Stationarity and geometric ergodicity of BEKK multivariate GARCH models. Stochastic Processes and Applications 121, 2331–2360.CrossRefGoogle Scholar
Chan, N.H. & Wei, C.Z. (1987) Asymptotic inference for nearly nonstationary AR(1) processes. Annals of Statistics 15, 1050–1063.CrossRefGoogle Scholar
Engle, R.F. (1982) Autoregressive conditional heteroscedasticity with estimates of the variance of the United Kingdom inflation. Econometrica 50, 987–1008.CrossRefGoogle Scholar
Francq, C. & Zakoian, J.-M. (2010) GARCH Models: Structure, Statistical Inference and Financial Applications. Wiley.CrossRefGoogle Scholar
Giraitis, L., Koul, H.L. & Surgailis, D. (2012) Large Sample Theory for Long Memory Processes. Imperial College Press.CrossRefGoogle Scholar
Hall, P. & Heyde, C.C. (1980) Martingale Limit Theory and its Application. Academic Press.Google Scholar
Horn, R.A. & Johnson, C.R. (2013) Matrix Analysis. Cambridge University Press.Google Scholar
Kostakis, A., Magdalinos, T., & Stamatogiannis, M.P. (2015a) Robust econometric inference for stock return predictability. Review of Financial Studies 28 (5), 1506–1553.CrossRefGoogle Scholar
Kostakis, A., Magdalinos, T., & Stamatogiannis, M.P. (2015b). Online Appendix to: Robust Econometric Inference for Stock Return Predictability.CrossRefGoogle Scholar
Ling, S. & Li, W.K. (1997a) Estimating and testing for unit root processes with GARCH(1,1) errors. Technical report, Department of Statistics, University of Hong Kong.Google Scholar
Ling, S. & Li, W.K. (1997b) On fractionally integrated autoregressive moving average time series models with conditional heteroskedasticity. Journal of the American Statistical Association 92, 1184–1194.CrossRefGoogle Scholar
Ling, S. & McAleer, M. (2003) Asymptotic theory for a vector ARMA-GARCH model. Econometric Theory 19, 280–310.CrossRefGoogle Scholar
Magdalinos, T. & Phillips, P.C.B. (2009) Limit theory for cointegrated systems with moderately integrated and moderately explosive regressors. Econometric Theory 25, 482–526.CrossRefGoogle Scholar
Magdalinos, T. & Phillips, P.C.B. (2020) Econometric Inference in Matrix Vicinities of Unity and Stationarity. Working paper.Google Scholar
Pantula, S.G. (1989) Estimation of autoregressive models with ARCH errors. Sankhya B 50, 119–138.Google Scholar
Phillips, P.C.B. (1987a) Towards a unified asymptotic theory for autoregression. Biometrika 74, 535–547.CrossRefGoogle Scholar
Phillips, P.C.B. (1987b) Time series regression with a unit root. Econometrica 55, 277–302.CrossRefGoogle Scholar
Phillips, P.C.B. (1988) Regression theory for near-integrated time series. Econometrica 56, 1021–1044.CrossRefGoogle Scholar
Phillips, P.C.B. & Magdalinos, T. (2007a) Limit theory for moderate deviations from a unit root. Journal of Econometrics 136, 115–130.CrossRefGoogle Scholar
Phillips, P.C.B. & Magdalinos, T. (2007b) Limit theory for moderate deviations from a unit root under weak dependence. In Phillips, G.D.A. and Tzavalis, E. (Eds.), The Refinement of Econometric Estimation and Test Procedures: Finite Sample and Asymptotic Analysis. Cambridge University Press, 123–162.CrossRefGoogle Scholar
Phillips, P.C.B. & Magdalinos, T. (2009a) Econometric Inference in the Vicinity of Unity. Working paper, Singapore Management University.Google Scholar
Phillips, P.C.B. & Magdalinos, T. (2009b) Unit root and cointegrating limit theory when the initialization is in the infinite past. Econometric Theory 25, 1682–1715.CrossRefGoogle Scholar
Phillips, P.C.B. & Solo, V. (1992) Asymptotics for linear processes. Annals of Statistics 20, 971–1001.CrossRefGoogle Scholar
Weiss, A.A. (1986) Asymptotic theory for ARCH models: estimation and testing. Econometric Theory 2, 107–131.CrossRefGoogle Scholar
White, H. (1980) A Heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica 48, 817–838.CrossRefGoogle Scholar