Published online by Cambridge University Press: 22 September 2015
Limit theory is developed for the dynamic panel IV estimator in the presence of an autoregressive root near unity. In the unit root case, Anderson–Hsiao lagged variable instruments satisfy orthogonality conditions but are well known to be irrelevant. For a fixed time series sample size (T) IV is inconsistent and approaches a shifted Cauchy-distributed random variate as the cross-section sample size n → ∞. But when T → ∞, either for fixed n or as n → ∞, IV is 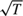 $\sqrt T$ consistent and its limit distribution is a ratio of random variables that converges to twice a standard Cauchy as n → ∞. In this case, the usual instruments are uncorrelated with the regressor but irrelevance does not prevent consistent estimation. The same Cauchy limit theory holds sequentially and jointly as (n, T) → ∞ with no restriction on the divergence rates of n and T. When the common autoregressive root
$\sqrt T$ consistent and its limit distribution is a ratio of random variables that converges to twice a standard Cauchy as n → ∞. In this case, the usual instruments are uncorrelated with the regressor but irrelevance does not prevent consistent estimation. The same Cauchy limit theory holds sequentially and jointly as (n, T) → ∞ with no restriction on the divergence rates of n and T. When the common autoregressive root 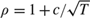 $\rho = 1 + c/\sqrt T$ the panel comprises a collection of mildly integrated time series. In this case, the IV estimator is
$\rho = 1 + c/\sqrt T$ the panel comprises a collection of mildly integrated time series. In this case, the IV estimator is 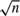 $\sqrt n$ consistent for fixed T and
$\sqrt n$ consistent for fixed T and 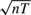 $\sqrt {nT}$ consistent with limit distribution N (0, 4) when (n, T) → ∞ sequentially or jointly. These results are robust for common roots of the form ρ = 1+c/Tγ for all γ ∈ (0, 1) and joint convergence holds. Limit normality holds but the variance changes when γ = 1. When γ > 1 joint convergence fails and sequential limits differ with different rates of convergence. These findings reveal the fragility of conventional Gaussian IV asymptotics to persistence in dynamic panel regressions.
$\sqrt {nT}$ consistent with limit distribution N (0, 4) when (n, T) → ∞ sequentially or jointly. These results are robust for common roots of the form ρ = 1+c/Tγ for all γ ∈ (0, 1) and joint convergence holds. Limit normality holds but the variance changes when γ = 1. When γ > 1 joint convergence fails and sequential limits differ with different rates of convergence. These findings reveal the fragility of conventional Gaussian IV asymptotics to persistence in dynamic panel regressions.
This paper originated in a Yale take home examination (Phillips, 2013). Some of the results were presented at a Conference in honor of Richard J. Smith’s 65th birthday at Cambridge University in May, 2014. The author acknowledges helpful comments from the referees and support from the NSF under Grant No. SES 12-58258.