Article contents
THE DICKEY–FULLER TEST FOR EXPONENTIAL RANDOM WALKS
Published online by Cambridge University Press: 04 August 2003
Abstract
A common test in econometrics is the Dickey–Fuller test, which
is based on the test statistic
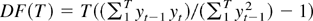 .
We investigate the behavior of the test statistic if the data
yt are given by an exponential random walk
exp(Zt) where
Zt =
Zt−1 +
σεt and the εt are
independent and identically distributed random variables. The test
statistic DF(T) is a nonlinear transformation of the
partial sums of εt process. Under certain
moment conditions on the εt we show that
.
We investigate the behavior of the test statistic if the data
yt are given by an exponential random walk
exp(Zt) where
Zt =
Zt−1 +
σεt and the εt are
independent and identically distributed random variables. The test
statistic DF(T) is a nonlinear transformation of the
partial sums of εt process. Under certain
moment conditions on the εt we show that
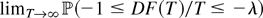 tends to one as λ → 0. For the particular case that the
εt define a simple random walk it is shown that
plimT→∞DF(T)/T exists and the limit is
evaluated. The theoretical results are illustrated by some simulation
experiments.We gratefully acknowledge the
help of an anonymous referee whose comments on the first two versions of
this paper enabled us to reduce the number of mistakes and to increase the
clarity of presentation. The authors' research was supported in part
by Sonderforschungsbereich 475, University of Dortmund.
tends to one as λ → 0. For the particular case that the
εt define a simple random walk it is shown that
plimT→∞DF(T)/T exists and the limit is
evaluated. The theoretical results are illustrated by some simulation
experiments.We gratefully acknowledge the
help of an anonymous referee whose comments on the first two versions of
this paper enabled us to reduce the number of mistakes and to increase the
clarity of presentation. The authors' research was supported in part
by Sonderforschungsbereich 475, University of Dortmund.
- Type
- Research Article
- Information
- Copyright
- © 2003 Cambridge University Press
References
REFERENCES
- 3
- Cited by


