Article contents
A Bootstrap Test for Positive Definiteness of Income Effect Matrices
Published online by Cambridge University Press: 18 October 2010
Abstract
Positive definiteness of income effect matrices provides a sufficient condition for the law of demand to hold. Given cross section household expenditure data, empirical evidence for the law of demand can be obtained by estimating such matrices. Härdle, Hildenbrand, and Jerison used the bootstrap method to simulate the distribution of the smallest eigenvalue of random matrices and to test their positive definiteness. Here, theoretical aspects of this bootstrap test of positive definiteness are considered. The asymptotic distribution of the smallest eigenvalue 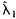 , of the matrix estimate is obtained. This theory applies generally to symmetric, asymptotically normal random matrices. A bootstrap approximation to the distribution of
, of the matrix estimate is obtained. This theory applies generally to symmetric, asymptotically normal random matrices. A bootstrap approximation to the distribution of 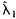 is shown to converge in probability to the asymptotic distribution of
is shown to converge in probability to the asymptotic distribution of 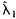 . The bootstrap test is illustrated using British family expenditure survey data.
. The bootstrap test is illustrated using British family expenditure survey data.
- Type
- Articles
- Information
- Copyright
- Copyright © Cambridge University Press 1992
References
REFERENCES
- 9
- Cited by


