Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-05T05:46:26.147Z Has data issue: false hasContentIssue false
  • English
  • Français

The Bahadur-Kiefer Representation of Lp Regression Estimators

Published online by Cambridge University Press:  11 February 2009

Miguel A. Arcones
Miguel A. Arcones
Affiliation:
University of Texas, Austin
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the following linear regression model:

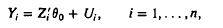
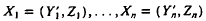where are independent and identically distributed random variables, Yi, is real, Zi has values in Rm, Ui, is independent of Zi, and θ0 is an m-dimensional parameter to be estimated. The Lp estimator of θ0 is the value 6n such that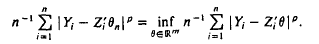

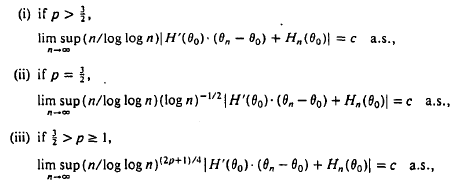
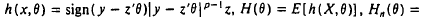
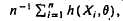Here, we will give the exact Bahadur-Kiefer representation of θn, for each p ≥ 1. Explicitly, we will see that, under regularity conditions,

where and c is a positive constant, which depends on p and on the random variable X.

Type
Research Article
Information
Econometric Theory , Volume 12 , Issue 2 , June 1996 , pp. 257 - 283
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arcones, M.A. (1994a) Necessary and Sufficient Conditions for the Law of the Iterated Logarithm of Triangular Arrays of Empirical Processes. Preprint.Google Scholar
Arcones, M.A. (1994b) On the weak Bahadur-Kiefer representation for M-estimators. In Hoffmann-Jørgensen, J., Kuelbs, J., & Marcus, M.B. (eds.), Probability in Banach Spaces, 9, pp. 357–372. Boston: Birkhäuser.CrossRefGoogle Scholar
Arcones, M.A. (1994c) Second Order Representations of the Least Absolute Deviation Regression Estimator. Preprint.Google Scholar
Arcones, M.A. (1994d) Some strong limit theorems for M-estimators. Stochastic Processes and Their Applications 53, 241–268.CrossRefGoogle Scholar
Aronszajn, N. (1950) Theory of reproducing kernels. Transactions of the American Mathematical Society 68, 337–404.CrossRefGoogle Scholar
Babu, G.J. (1989) Some strong representations for LAD estimators in linear models. Probability Theory and Related Fields 83, 547–558.CrossRefGoogle Scholar
Bai, Z.D., Radhakrishna Rao, C. & Wu, Y. (1992) M-estimation of multivariate linear regression parameters under a convex discrepancy function. Statistica Sinica 2, 237–254.Google Scholar
Bassett, G. & Koenker, R. (1978) Asymptotic theory of least absolute error regression. Journal of the American Statistical Association 73, 618–622.CrossRefGoogle Scholar
Chaudhuri, H. (1984) Nonparametric estimates of regression quantiles and their local Bahadur representation. Annals of Statistics 19, 760–777.Google Scholar
Dudley, R.M. (1984). A course on empirical processes. Lecture Notes in Mathematics 1097, 1–142. New York: Springer-Verlag.Google Scholar
Haberman, S.J. (1989). Concavity and estimation. Annals of Statistics 17, 1631–1661.CrossRefGoogle Scholar
He, X. & Shao, Q.M. (1993) A Strong Bahadur-Kiefer Representation of Lp Regression Estimators. Preprint.Google Scholar
He, X. & Shao, Q.M. (1995) An Improved Bahadur Representation of M-estimators and Its Application to Linear Regression with Nonstochastic Designs. Preprint.CrossRefGoogle Scholar
Huber, P.J. (1967) The behaviour of maximum likelihood estimates under non-standard condition. In Neyman, J. (ed.), Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, vol. 1, pp. 221–233. Berkeley: University of California Press.Google Scholar
Jurečková, J. (1977) Asymptotic relations of M-estimates and R-estimates in linear regression model. Annals of Statistics 5, 464–472.CrossRefGoogle Scholar
Jurečková, J. & Sen, P.K. (1989) Uniform second order asymptotic linearity of M-statistics in linear models. Statistics & Decisions 7, 263–276.Google Scholar
Koenker, R. & Portnoy, S. (1987) L-estimation for linear models. Journal of the American Statistical Association 82, 851–857.Google Scholar
Ledoux, M. & Talagrand, M. (1988) Characterization of the law of the iterated logarithm in Banach spaces. Annals of Probability 16, 1242–1264.CrossRefGoogle Scholar
Pollard, D. (1984) Convergence of Stochastic Processes. New York: Springer-Verlag.CrossRefGoogle Scholar
Pollard, D. (1991) Asymptotics for least absolute deviation regression estimators. Econometric Theory 7, 186–199.CrossRefGoogle Scholar
Rousseeuw, P.J. & Leroy, A.M. (1987) Robust Regression and Outlier Detection, New York: John Wiley & Sons.CrossRefGoogle Scholar
Ruppert, D. & Carroll, RJ. (1980) Trimmed least squares estimation in the linear model. Journal of the American Statistical Association 75, 828–838.CrossRefGoogle Scholar
Sposito, V.A. (1990) Some properties of i.p-estimates. In Lawrence, K.D. & Arthur, J.L. (eds.), Robust Regression, Analysis and Applications, pp. 23–58. New York: Marcel Dekker.Google Scholar
Stone, C.J. (1982) Optimal global rates of convergence for nonparametric regression. Annals of Statistics 10, 1040–1063.CrossRefGoogle Scholar