Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gilboa, Itzhak
Lieberman, Offer
and
Schmeidler, David
2011.
A similarity-based approach to prediction.
Journal of Econometrics,
Vol. 162,
Issue. 1,
p.
124.
Teitelbaum, Joshua C.
2012.
Analogical Legal Reasoning: Theory and Evidence.
SSRN Electronic Journal,
Lieberman, Offer
2012.
A similarity‐based approach to time‐varying coefficient non‐stationary autoregression.
Journal of Time Series Analysis,
Vol. 33,
Issue. 3,
p.
484.
Lieberman, Offer
and
Phillips, Peter C. B.
2013.
Norming Rates and Limit Theory for Some Time-Varying Coefficient Autoregressions.
SSRN Electronic Journal,
Teitelbaum, Joshua C.
2013.
Asymmetric Empirical Similarity.
SSRN Electronic Journal,
Teitelbaum, Joshua C.
2013.
Asymmetric empirical similarity.
Mathematical Social Sciences,
Vol. 66,
Issue. 3,
p.
346.
Bordley, Robert F.
2014.
Reference Class Forecasting: Resolving Its Challenge to Statistical Modeling.
The American Statistician,
Vol. 68,
Issue. 4,
p.
221.
Lieberman, Offer
and
Phillips, Peter C. B.
2014.
NORMING RATES AND LIMIT THEORY FOR SOME TIME‐VARYING COEFFICIENT AUTOREGRESSIONS.
Journal of Time Series Analysis,
Vol. 35,
Issue. 6,
p.
592.
Kapetanios, George
Mitchell, James
and
Shin, Yongcheol
2014.
A nonlinear panel data model of cross-sectional dependence.
Journal of Econometrics,
Vol. 179,
Issue. 2,
p.
134.
Lieberman, Offer
and
Phillips, Peter C. B.
2014.
A Multivariate Stochastic Unit Root Model with an Application to Derivative Pricing.
SSRN Electronic Journal,
Golosnoy, Vasyl
Hamid, Alain
and
Okhrin, Yarema
2014.
The empirical similarity approach for volatility prediction.
Journal of Banking & Finance,
Vol. 40,
Issue. ,
p.
321.
Kinjo, Keita
and
Sugawara, Shinya
2015.
Predicting Empirical Patterns in Viewing Japanese TV Dramas Using Case-Based Decision Theory.
SSRN Electronic Journal,
Melo, Oscar O.
Melo, Carlos E.
and
Mateu, Jorge
2015.
Distance-based beta regression for prediction of mutual funds.
AStA Advances in Statistical Analysis,
Vol. 99,
Issue. 1,
p.
83.
Hamid, Alain
2015.
Prediction power of high-frequency based volatility measures: a model based approach.
Review of Managerial Science,
Vol. 9,
Issue. 3,
p.
549.
Hamid, Alain
and
Heiden, Moritz
2015.
Forecasting volatility with empirical similarity and Google Trends.
Journal of Economic Behavior & Organization,
Vol. 117,
Issue. ,
p.
62.
Teitelbaum, J. C.
2015.
Analogical Legal Reasoning: Theory and Evidence.
American Law and Economics Review,
Vol. 17,
Issue. 1,
p.
160.
Kinjo, Keita
and
Sugawara, Shinya
2016.
Predicting Empirical Patterns in Viewing Japanese TV Dramas Using Case-Based Decision Theory.
The B.E. Journal of Theoretical Economics,
Vol. 16,
Issue. 2,
Golosnoy, Vasyl
and
Pape, Markus
2016.
How Much Would Banks Pay?.
SSRN Electronic Journal ,
Lieberman, Offer
and
Phillips, Peter C.B.
2017.
A multivariate stochastic unit root model with an application to derivative pricing.
Journal of Econometrics,
Vol. 196,
Issue. 1,
p.
99.
Durán Bustamante, Mario
Hernandez del Valle, Adrian
and
Ortiz Ramírez, Ambrosio
2018.
The Google trends effect on the behavior of the exchange rate Mexican peso - US dollar.
Contaduría y Administración,
Vol. 64,
Issue. 2,
p.
103.
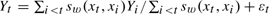 , t = 2, …, n, where sw(xt, xi) is a similarity function between the tth and the ith observations and {εt} is a random disturbance term. This process was originally axiomatized by Gilboa, Lieberman, and Schmeidler (2006, Review of Economics and Statistics 88, 433–444) as a way by which agents, or even nature, reason. In the present paper, consistency and the asymptotic distribution of the quasi-maximum likelihood estimator of the parameters of the model are established. Connections to other models and techniques are drawn. In its general form, the model does not fall within any class of nonstationary econometric models for which asymptotic theory is available. For this reason, the developments in this paper are new and nonstandard.
, t = 2, …, n, where sw(xt, xi) is a similarity function between the tth and the ith observations and {εt} is a random disturbance term. This process was originally axiomatized by Gilboa, Lieberman, and Schmeidler (2006, Review of Economics and Statistics 88, 433–444) as a way by which agents, or even nature, reason. In the present paper, consistency and the asymptotic distribution of the quasi-maximum likelihood estimator of the parameters of the model are established. Connections to other models and techniques are drawn. In its general form, the model does not fall within any class of nonstationary econometric models for which asymptotic theory is available. For this reason, the developments in this paper are new and nonstandard.

