Article contents
Asymptotic Expansions of the Distributions of Statistics Related to the Spectral Density Matrix in Multivariate Time Series and Their Applications
Published online by Cambridge University Press: 11 February 2009
Abstract
Let {X(t)} be a multivariate Gaussian stationary process with the spectral density matrix f0(ω), where θ is an unknown parameter vector. Using a quasi-maximum likelihood estimator 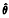 of θ, we estimate the spectral density matrix f0(ω) by f
of θ, we estimate the spectral density matrix f0(ω) by f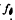 (ω). Then we derive asymptotic expansions of the distributions of functions of f
(ω). Then we derive asymptotic expansions of the distributions of functions of f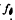 (ω). Also asymptotic expansions for the distributions of functions of the eigenvalues of f
(ω). Also asymptotic expansions for the distributions of functions of the eigenvalues of f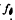 (ω) are given. These results can be applied to many fundamental statistics in multivariate time series analysis. As an example, we take the reduced form of the cobweb model which is expressed as a two-dimensional vector autoregressive process of order 1 (AR(1) process) and show the asymptotic distribution of
(ω) are given. These results can be applied to many fundamental statistics in multivariate time series analysis. As an example, we take the reduced form of the cobweb model which is expressed as a two-dimensional vector autoregressive process of order 1 (AR(1) process) and show the asymptotic distribution of 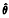 , the estimated coherency, and contribution ratio in the principal component analysis based on
, the estimated coherency, and contribution ratio in the principal component analysis based on 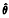 in the model, up to the second-order terms. Although our general formulas seem very involved, we can show that they are tractable by using REDUCE 3.
in the model, up to the second-order terms. Although our general formulas seem very involved, we can show that they are tractable by using REDUCE 3.
- Type
- Articles
- Information
- Copyright
- Copyright © Cambridge University Press 1990
References
- 2
- Cited by


