Published online by Cambridge University Press: 09 April 2017
We extend the 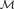 ${\cal M}$ class of unit root tests introduced by Stock (1999, Cointegration, Causality and Forecasting. A Festschrift in Honour of Clive W.J. Granger. Oxford University Press), Perron and Ng (1996, Review of Economic Studies 63, 435–463) and Ng and Perron (2001, Econometrica 69, 1519–1554) to the seasonal case, thereby developing semi-parametric alternatives to the regression-based augmented seasonal unit root tests of Hylleberg, Engle, Granger, and Yoo (1990, Journal of Econometrics 44, 215–238). The success of this class of unit root tests to deliver good finite sample size control even in the most problematic (near-cancellation) case where the shocks contain a strong negative moving average component is shown to carry over to the seasonal case as is the superior size/power trade-off offered by these tests relative to other available tests.
${\cal M}$ class of unit root tests introduced by Stock (1999, Cointegration, Causality and Forecasting. A Festschrift in Honour of Clive W.J. Granger. Oxford University Press), Perron and Ng (1996, Review of Economic Studies 63, 435–463) and Ng and Perron (2001, Econometrica 69, 1519–1554) to the seasonal case, thereby developing semi-parametric alternatives to the regression-based augmented seasonal unit root tests of Hylleberg, Engle, Granger, and Yoo (1990, Journal of Econometrics 44, 215–238). The success of this class of unit root tests to deliver good finite sample size control even in the most problematic (near-cancellation) case where the shocks contain a strong negative moving average component is shown to carry over to the seasonal case as is the superior size/power trade-off offered by these tests relative to other available tests.
We are grateful to the Editor, Peter Phillips, the Co-Editor, Michael Jansson and two anonymous referees for their helpful and constructive comments. Tomás del Barrio Castro acknowledges financial support from projects ECO2011-23934 and ECO2014-58991-C3-3-R.