Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-12T11:02:10.277Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ROLE OF INITIAL VALUES IN CONDITIONAL SUM-OF-SQUARES ESTIMATION OF NONSTATIONARY FRACTIONAL TIME SERIES MODELS

Published online by Cambridge University Press:  11 May 2015

Søren Johansen  and
Morten Ørregaard Nielsen
Søren Johansen
Affiliation:
University of Copenhagen and CREATES
Morten Ørregaard Nielsen*
Affiliation:
Queen’s University and CREATES
*
*Address correspondence to Morten Ørregaard Nielsen, Department of Economics, Dunning Hall, Queen’s University, Kingston, Ontario K7L 3N6, Canada; email: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we analyze the influence of observed and unobserved initial values on the bias of the conditional maximum likelihood or conditional sum-of-squares (CSS, or least squares) estimator of the fractional parameter, d, in a nonstationary fractional time series model. The CSS estimator is popular in empirical work due, at least in part, to its simplicity and its feasibility, even in very complicated nonstationary models.

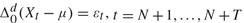We consider a process, Xt, for which data exist from some point in time, which we call –N0 + 1, but we only start observing it at a later time, t = 1. The parameter (d, μ, σ2) is estimated by CSS based on the model ${\rm{\Delta }}_0^d \left( {X_t - \mu } \right) = \varepsilon _t ,t = N + 1, \ldots ,N + T$, conditional on X1,..., XN. We derive an expression for the second-order bias of 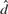$\hat d$ as a function of the initial values, Xt, t = – N0 + 1,..., N, and we investigate the effect on the bias of setting aside the first N observations as initial values. We compare 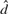$\hat d$ with an estimator, 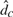$\hat d_c $, derived similarly but by choosing μ = C. We find, both theoretically and using a data set on voting behavior, that in many cases, the estimation of the parameter μ picks up the effect of the initial values even for the choice N = 0.

If N0 = 0, we show that the second-order bias can be completely eliminated by a simple bias correction. If, on the other hand, N0 > 0, it can only be partly eliminated because the second-order bias term due to the initial values can only be diminished by increasing N.

Type
ARTICLES
Information
Econometric Theory , Volume 32 , Issue 5 , October 2016 , pp. 1095 - 1139
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abramowitz, M. & Stegun, I.A. (1964) Handbook of Mathematical Functions. National Bureau of Standards.Google Scholar
Andersen, T.G., Bollerslev, T., Diebold, F.X., & Ebens, H. (2001) The distribution of daily realized stock return volatility. Journal of Financial Economics 61, 43–76.CrossRefGoogle Scholar
Askey, R. (1975) Orthogonal Polynomials and Special Functions. SIAM.CrossRefGoogle Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley.Google Scholar
Bingham, N.H., Goldie, C.M., & Teugels, J.L. (1987) Regular Variation. Cambridge University Press.CrossRefGoogle Scholar
Bollerslev, T., Osterrieder, D., Sizova, N., & Tauchen, G. (2013) Risk and return: Long-run relationships, fractional cointegration, and return predictability. Journal of Financial Economics 108, 409–424.CrossRefGoogle Scholar
Box, G.E.P. & Jenkins, G.M. (1970) Time Series Analysis, Forecasting, and Control. Holden-Day.Google Scholar
Byers, J.D., Davidson, J., & Peel, D. (1997) Modelling political popularity: An analysis of long-range dependence in opinion poll series. Journal of the Royal Statistical Society, Series A 160, 471–490.CrossRefGoogle Scholar
Carlini, F., Manzoni, M., & Mosconi, R. (2010) The Impact of Supply and Demand Imbalance on Stock Prices: An Analysis Based on Fractional Cointegration using Borsa Italiana Ultra High Frequency Data. Working paper, Politecnico di Milano.Google Scholar
Davidson, J. & Hashimzade, N. (2009) Type I and type II fractional Brownian motions: A reconsideration. Computational Statistics & Data Analysis 53, 2089–2106.CrossRefGoogle Scholar
Dolado, J.J., Gonzalo, J., & Mayoral, L. (2002) A fractional Dickey-Fuller test for unit roots. Econometrica 70, 1963–2006.CrossRefGoogle Scholar
Doornik, J.A. & Ooms, M. (2003) Computational aspects of maximum likelihood estimation of autoregressive fractionally integrated moving average models. Computational Statistics & Data Analysis 42, 333–348.CrossRefGoogle Scholar
Giraitis, L. & Taqqu, M. (1998) Central limit theorems for quadratic forms with time domain conditions. Annals of Probability 26, 377–398.CrossRefGoogle Scholar
Hualde, J. & Robinson, P.M. (2011) Gaussian pseudo-maximum likelihood estimation of fractional time series models. Annals of Statistics 39, 3152–3181.CrossRefGoogle Scholar
Jensen, A.N. & Nielsen, M.Ø. (2014) A fast fractional difference algorithm. Journal of Time Series Analysis 35, 428–436.CrossRefGoogle Scholar
Johansen, S. & Nielsen, M.Ø. (2010) Likelihood inference for a nonstationary fractional autoregressive model. Journal of Econometrics 158, 51–66.CrossRefGoogle Scholar
Johansen, S. & Nielsen, M.Ø. (2012a) Likelihood inference for a fractionally cointegrated vector autoregressive model. Econometrica 80, 2667–2732.Google Scholar
Johansen, S. & Nielsen, M.Ø. (2012b) A necessary moment condition for the fractional functional central limit theorem. Econometric Theory 28, 671–679.CrossRefGoogle Scholar
Lawley, D.N. (1956) A general method for approximating to the distribution of likelihood ratio criteria. Biometrika 43, 295–303.CrossRefGoogle Scholar
Li, W.K. & McLeod, A.I. (1986) Fractional time series modelling. Biometrika 73, 217–221.CrossRefGoogle Scholar
Lieberman, O. & Phillips, P.C.B. (2004) Expansions for the distribution of the maximum likelihood estimator of the fractional difference parameter. Econometric Theory 20, 464–484.CrossRefGoogle Scholar
Marinucci, D. & Robinson, P.M. (2000) Weak convergence of multivariate fractional processes. Stochastic Processes and their Applications 86, 103–120.CrossRefGoogle Scholar
Nielsen, M.Ø. (2015) Asymptotics for the conditional-sum-of-squares estimator in multivariate fractional time series models. Journal of Time Series Analysis 36, 154–188.CrossRefGoogle Scholar
Osterrieder, D. & Schotman, P.C. (2011) Predicting Returns with a Co-fractional VAR Model. CREATES research paper, Aarhus University.CrossRefGoogle Scholar
Robinson, P.M. (1994) Efficient tests of nonstationary hypotheses. Journal of the American Statistical Association 89, 1420–1437.CrossRefGoogle Scholar
Rossi, E. & Santucci de Magistris, P. (2013) A no-arbitrage fractional cointegration model for futures and spot daily ranges. Journal of Futures Markets 33, 77–102.CrossRefGoogle Scholar
Sowell, F. (1992) Maximum likelihood estimation of stationary univariate fractionally integrated time series models. Journal of Econometrics 53, 165–188.CrossRefGoogle Scholar
Tschernig, R., Weber, E., & Weigand, R. (2013) Long-run identification in a fractionally integrated system. Journal of Business and Economic Statistics 31, 438–450.CrossRefGoogle Scholar