Article contents
A PERMUTATION-BASED ESTIMATOR FOR MONOTONE INDEX MODELS
Published online by Cambridge University Press: 03 April 2008
Abstract
This paper shows that the finite-dimensional parameters of a monotone-index model can be estimated by minimizing an objective function based on sorting the data. The key observation guiding this procedure is that the sum of distances between pairs of adjacent observations is minimized (over all possible permutations) when the observations are sorted by their values. The resulting estimator is a generalization of Cavanagh and Sherman's monotone rank estimator (MRE) (Cavanagh and Sherman, 1998, Journal of Econometrics 84, 351–381) and does not require a bandwidth choice. The estimator is 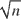 -consistent and asymptotically normal with a consistently estimable covariance matrix. This least-squares estimator can also be used to estimate monotone-index panel data models. A Monte Carlo study is presented where the proposed estimator is seen to dominate the MRE in terms of mean-squared error and mean absolute deviation.
-consistent and asymptotically normal with a consistently estimable covariance matrix. This least-squares estimator can also be used to estimate monotone-index panel data models. A Monte Carlo study is presented where the proposed estimator is seen to dominate the MRE in terms of mean-squared error and mean absolute deviation.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 2008
References
REFERENCES
- 6
- Cited by


