Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pesaran, M. Hashem
and
Tosetti, Elisa
2011.
Large panels with common factors and spatial correlation.
Journal of Econometrics,
Vol. 161,
Issue. 2,
p.
182.
Arbia, Giuseppe
2011.
A Lustrum of SEA: Recent Research Trends Following the Creation of the Spatial Econometrics Association (2007–2011).
Spatial Economic Analysis,
Vol. 6,
Issue. 4,
p.
377.
Baylis, Kathy
Paulson, Nicholas D.
and
Piras, Gianfranco
2011.
Spatial Approaches to Panel Data in Agricultural Economics: A Climate Change Application.
Journal of Agricultural and Applied Economics,
Vol. 43,
Issue. 3,
p.
325.
Cizek, Pavel
Jacobs, Jan P. A. M.
Ligthart, Jenny E.
and
Vrijburg, Hendrik
2011.
GMM Estimation of Fixed Effects Dynamic Panel Data Models with Spatial Lag and Spatial Errors.
SSRN Electronic Journal,
Yu, Jihai
de Jong, Robert
and
Lee, Lung-fei
2012.
Estimation for spatial dynamic panel data with fixed effects: The case of spatial cointegration.
Journal of Econometrics,
Vol. 167,
Issue. 1,
p.
16.
Lee, Lung‐fei
and
Yu, Jihai
2012.
SPATIAL PANELS: RANDOM COMPONENTS VERSUS FIXED EFFECTS*.
International Economic Review,
Vol. 53,
Issue. 4,
p.
1369.
Piras, Gianfranco
2013.
Efficient GMM Estimation of a Cliff and Ord Panel Data Model with Random Effects.
Spatial Economic Analysis,
Vol. 8,
Issue. 3,
p.
370.
Dubé, Jean
and
Legros, Diègo
2013.
Dealing with spatial data pooled over time in statistical models.
Letters in Spatial and Resource Sciences,
Vol. 6,
Issue. 1,
p.
1.
Ko, Kwan Wai
and
Mok, Kin Wai Patrick
2014.
Clustering of cultural industries in Chinese cities.
Economics of Transition,
Vol. 22,
Issue. 2,
p.
365.
Lee, Lung-fei
and
Yu, Jihai
2014.
Efficient GMM estimation of spatial dynamic panel data models with fixed effects.
Journal of Econometrics,
Vol. 180,
Issue. 2,
p.
174.
Xie, Wei
2015.
Spatial Panel VAR and Application to Forecast Influenza Incidence Rates of US States.
SSRN Electronic Journal ,
Su, Liangjun
and
Yang, Zhenlin
2015.
QML estimation of dynamic panel data models with spatial errors.
Journal of Econometrics,
Vol. 185,
Issue. 1,
p.
230.
Yang, Zhenlin
Yu, Jihai
and
Liu, Shew Fan
2016.
Bias correction and refined inferences for fixed effects spatial panel data models.
Regional Science and Urban Economics,
Vol. 61,
Issue. ,
p.
52.
Arbués, Ignacio
Ledo, Ramiro
and
Matilla-García, Mariano
2016.
Automatic Identification of General Vector Error Correction Models.
Economics,
Vol. 10,
Issue. 1,
Kelejian, Harry H.
and
Piras, Gianfranco
2016.
An Extension of the J‐Test to a Spatial Panel Data Framework.
Journal of Applied Econometrics,
Vol. 31,
Issue. 2,
p.
387.
Kelejian, Harry H.
and
Piras, Gianfranco
2016.
A J test for dynamic panel model with fixed effects, and nonparametric spatial and time dependence.
Empirical Economics,
Vol. 51,
Issue. 4,
p.
1581.
Taşpınar, Süleyman
Doğan, Osman
and
Bera, Anil K.
2017.
GMM gradient tests for spatial dynamic panel data models.
Regional Science and Urban Economics,
Vol. 65,
Issue. ,
p.
65.
Qu, Xi
Lee, Lung-fei
and
Yu, Jihai
2017.
QML estimation of spatial dynamic panel data models with endogenous time varying spatial weights matrices.
Journal of Econometrics,
Vol. 197,
Issue. 2,
p.
173.
Hory, Marie-Pierre
2018.
Delayed mimicking: the timing of fiscal interactions in Europe.
European Journal of Political Economy,
Vol. 55,
Issue. ,
p.
97.
Yang, Zhenlin
2018.
Unified M-estimation of fixed-effects spatial dynamic models with short panels.
Journal of Econometrics,
Vol. 205,
Issue. 2,
p.
423.
 consistent and the estimates of other parameters are
consistent and the estimates of other parameters are 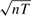 consistent, and all of them are asymptotically normal. For the latter model the sum of the contemporaneous spatial effect and dynamic spatial effect converges at
consistent, and all of them are asymptotically normal. For the latter model the sum of the contemporaneous spatial effect and dynamic spatial effect converges at  rate. We also propose a bias-correction procedure so that the asymptotic biases of those estimates are eliminated as long as n/T3 → 0.
rate. We also propose a bias-correction procedure so that the asymptotic biases of those estimates are eliminated as long as n/T3 → 0.

