Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-27T19:23:11.336Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Expansions of the Distributions of Statistics Related to the Spectral Density Matrix in Multivariate Time Series and Their Applications

Published online by Cambridge University Press:  11 February 2009

Masanobu Taniguchi  and
Koichi Maekawa
Masanobu Taniguchi
Affiliation:
Hiroshima University
Koichi Maekawa
Affiliation:
Hiroshima University
Get access Rights & Permissions [Opens in a new window]

Abstract

Let {X(t)} be a multivariate Gaussian stationary process with the spectral density matrix f0(ω), where θ is an unknown parameter vector. Using a quasi-maximum likelihood estimator 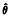of θ, we estimate the spectral density matrix f0(ω) by f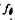(ω). Then we derive asymptotic expansions of the distributions of functions of f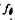(ω). Also asymptotic expansions for the distributions of functions of the eigenvalues of f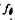(ω) are given. These results can be applied to many fundamental statistics in multivariate time series analysis. As an example, we take the reduced form of the cobweb model which is expressed as a two-dimensional vector autoregressive process of order 1 (AR(1) process) and show the asymptotic distribution of 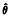, the estimated coherency, and contribution ratio in the principal component analysis based on 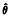in the model, up to the second-order terms. Although our general formulas seem very involved, we can show that they are tractable by using REDUCE 3.

Type
Articles
Information
Econometric Theory , Volume 6 , Issue 1 , March 1990 , pp. 75 - 96
Copyright
Copyright © Cambridge University Press 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Amos, D.E. & Koopmans, L.H.. Tables of the distribution of the coefficient of coherence of stationary bivariate Gaussian process. Sandia Corp. Monograph SCR-483. Sandia Corp. (The table is reprinted in Koopmans [12].)Google Scholar
2.Brillinger, D.R.Asymptotic properties of spectral estimates of second order. Biometrika 56 (1969): 375–390.CrossRefGoogle Scholar
3.Brillinger, D.R.Time series: data analysis and theory. New York: Holden-Day. 1975.Google Scholar
4.Fang, C. & Krishnaiah, P.R.. Asymptotic distributions of functions of the eigenvalues of some random matrices for nonnormal populations. Journal of Multivariate Analysis (12 (1982): 39–63.CrossRefGoogle Scholar
5.Fishman, G.S.Spectral methods in econometrics. Cambridge: Harvard University Press, 1969.CrossRefGoogle Scholar
6.Fujikoshi, Y. Asymptotic expansions for the distributions for some multivariate tests. In Krishnaiah, P.R. (ed.), Multivariate Analysis IV. Amsterdam-North-Holland, 1977.Google Scholar
7.Fujikoshi, Y.Asymptotic expansions for the distributions for some functions of the latent roots of matrices in three situations. Journal of Multivariate Analysis 8 (1978): 63–72. Erratum 10 (1980): 14.Google Scholar
8.Fuller, W.A.Introduction to statistical time series. New York: Wiley, 1976.Google Scholar
9.Granger, C.W.J. & Hatanaka, M.. Spectral analysis of time series. Princeton: Princeton University Press, 1964.Google Scholar
10.Hannan, E.J.Multiple time series. New York: Wiley, 1970.Google Scholar
11.Harvey, A.C.The economic analysis of time series. Oxford: Philip Allan Publishers Limited, 1981.Google Scholar
12.Hosoya, Y. & Taniguchi, M.. A central limit theorem for stationary processes and the parameter estimations of linear processes. Annals of Statistics 10 (1982): 132–153.Google Scholar
13.Koopmans, L.H.The spectral analysis of time series. New York: Academic Press, 1974.Google Scholar
14.Krishnaiah, P.R. & Lee, J.C.. On the asymptotic joint distributions of certain functions of the eigenvalues of four random matrices. Journal of Multivariate Analysis 9 (1979): 248–258.CrossRefGoogle Scholar
15.Phillips, P.C.B. & Ouliaris, S.. Testing for cointegration using principal components methods. Journal of Economic Dynamics and Control 12 (1988): 205–230.Google Scholar
16.Priestley, M.B., Rao, T., & Tong, H.. Identification of the structure of multivariate stochastic systems. In Krishnaiah, P.R. (ed.), Multivariate Analysis-Ill. New York: Academic, 1973.Google Scholar
17.Taniguchi, M.On the second order asymptotic efficiency of estimators of Gaussian ARMA processes. Annals of Statistics 11 (1983): 157–169.Google Scholar
18.Taniguchi, M.An asymptotic expansion for the distribution of the likelihood ratio criterion for a Gaussian autoregressive moving average process under a local alternative. Econometric Theory 1 (1985): 73–84.Google Scholar
19.Taniguchi, M.Third order asymptotic properties of maximum likelihood estimators for Gaussian ARMA process. Journal of Multivariate Analysis 18 (1986): 1–31.Google Scholar
20.Taniguchi, M. & Krishnaiah, P.R.. Asymptotic distributions of functions of the eigenvalues of sample covariance matrix and canonical correlation matrix in multivariate time series. Journal of Multivariate Analysis 22 (1987): 156–176.CrossRefGoogle Scholar