Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T20:20:32.441Z Has data issue: false hasContentIssue false
  • English
  • Français

JASMIN-based Two-dimensional Adaptive Combined Preconditioner for Radiation Diffusion Equations in Inertial Fusion Research

Part of: Partial differential equations, boundary value problems Computer aspects of numerical algorithms Numerical linear algebra

Published online by Cambridge University Press:  07 September 2017

Xiaoqiang Yue ,
Xiaowen Xu  and
Shi Shu
Xiaoqiang Yue
Affiliation:
School of Mathematics and Computational Science, Xiangtan University, Hunan 411105, China
Xiaowen Xu
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing 100088, China
Shi Shu*
Affiliation:
School of Mathematics and Computational Science, Xiangtan University, Hunan 411105, China
*
*Corresponding author. Email address:[email protected] (S. Shu)
Get access

Abstract

We present a JASMIN-based two-dimensional parallel implementation of an adaptive combined preconditioner 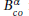for the solution of linear problems arising in the finite volume discretisation of one-group and multi-group radiation diffusion equations. We first propose the attribute of patch-correlation for cells of a two-dimensional monolayer piecewise rectangular structured grid without any suspensions based on the patch hierarchy of JASMIN, classify and reorder these cells via their attributes, and derive the conversion of cell-permutations. Using two cell-permutations, we then construct some parallel incomplete LU factorisation and substitution algorithms, to provide our parallel 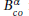-GMRES solver with the help of the default BoomerAMG in the HYPRE library. Numerical results demonstrate that our proposed parallel incomplete LU preconditioner (ILU) is of higher efficiency than the counterpart in the Euclid library, and that the proposed parallel 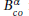-GMRES solver is more robust and more efficient than the default BoomerAMG-GMRES solver.

Keywords

Radiation diffusion equationscombined preconditioneradaptive technologyparallel computingJASMIN

MSC classification

Secondary: 65F10: Iterative methods for linear systems 65N55: Multigrid methods; domain decomposition 65Y05: Parallel computation 65Z05: Applications to physics
Type
Research Article
Information
East Asian Journal on Applied Mathematics , Volume 7 , Issue 3 , August 2017 , pp. 495 - 507
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Pei, W.B., The construction of simulation algorithms for laser fusion, Commun. Comput. Phys. 2, 255–270 (2007).Google Scholar
[2] Yue, X.Q., Shu, S., Xu, X.W. and Zhou, Z.Y., An adaptive combined preconditioner with applications in radiation diffusion equations, Commun. Comput. Phys. 18, 1313–1335 (2015).Google Scholar
[3] Pomraning, G.C., The Equations of Radiation Hydrodynamics, Pergamon (1973).Google Scholar
[4] Haines, B.M., Grinstein, F.F. and Fincke, J.R., Three-dimensional simulation strategy to determine the effects of turbulent mixing on inertial-confinement-fusion capsule performance, Phys. Rev. Lett. 89, 053302 (2014).Google Scholar
[5] Baldwin, C., Brown, P.N., Falgout, R., Graziani, F. and Jones, J., Iterative linear solvers in 2D radiation-hydrodynamics code: Methods and performance, J. Comput. Phys. 154, 1–40 (1999).CrossRefGoogle Scholar
[6] Xiao, Y.X., Shu, S., Zhang, P.W., Mo, Z.Y. and Xu, J., A kind of semi-coarsing AMG method for two dimensional energy equations with three temperatures, J. Numer. Meth. Comput. Appl. 24, 293–303 (2003).Google Scholar
[7] Mo, Z.Y., Parallel adaptive solution for two dimensional 3-T energy equation on UG, Comput. Visual Sci. 9, 165–174 (2006).Google Scholar
[8] Jiang, J., Huang, Y., Shu, S. and Zeng, S., Some new discretiztion and adaptation and multigrid methods for 2-D 3-T diffusion equations, J. Comput. Phys. 224, 168–181 (2007).Google Scholar
[9] Zhou, Z.Y., Xu, X.W., Shu, S., Feng, C.S. and Mo, Z.Y., An adaptive two-level preconditioner for 2-D 3-T radiation diffusion equations, Chin. J. Comput. Phys. 29, 475–483 (2012).Google Scholar
[10] Saad, Y., Iterative Methods for Sparse Linear Systems, SIAM (2003).Google Scholar
[11] Hysom, D. and Pothen, A., A scalable parallel algorithm for incomplete factor preconditioning, SIAM J. Sci. Comput. 22, 2194–2215 (2001).CrossRefGoogle Scholar
[12] Brandt, A., Multi-level adaptive solutions to boundary value problems, Math. Comput. 31, 333–390 (1977).CrossRefGoogle Scholar
[13] Ruge, J.W. and K. Stüben, Algebraic multigrid, in multigrid methods, Front. Appl. Math. 3, 73–130 (1987).Google Scholar
[14] Zhou, J., Hu, X. Z., Zhong, L.Q., Shu, S. and Chen, L., Two-grid methods for Maxwell eigenvalue problems, SIAM J. Numer. Anal. 52, 2027–2047 (2014).Google Scholar
[15] Xiao, Y., Zhou, Z. and Shu, S., An efficient algebraic multigrid method for quadratic discretizations of linear elasticity problems on some typical anisotropic meshes in three dimensions, Numer. Linear Algebra Appl. 22, 465–482 (2015).Google Scholar
[16] Hu, Q.Y., Shu, S. and Wang, J.X., Nonoverlapping domain decomposition methods with a simple coarse space for elliptic problems, Math. Comput. 79 (272), 2059–2078 (2010).Google Scholar
[17] Li, Y.H., Shu, S., Xu, Y.S., and Zou, Q.S., Multilevel preconditioning for the finite volume method, Math. Comput. 81 (279), 1399–1428 (2012).Google Scholar
[18] Hu, X.Z., Wu, S.H., Wu, X.H., Xu, J., Zhang, C.S., Zhang, S.Q. and Zikatanov, L., Combined pre-conditioning with applications in reservoir simulation, Multiscale Model. Simul. 11, 507–521 (2013).Google Scholar
[19] Mo, Z.Y., Zhang, A.Q., Cao, X.L., Liu, Q.K., Xu, X.W., An, H.B., Pei, W.B. and Zhu, S.P., JASMIN: A parallel software infrastructure for scientific computing, Front. Comput. Sci. 4, 480–488 (2010).CrossRefGoogle Scholar
[20] Cao, X.L., Mo, Z.Y., Liu, X., Xu, X.W., and Zhang, A.Q., Parallel implementation of fast multipole method based on JASMIN, Sci. China. Inf. Sci. 54, 757–766 (2011).CrossRefGoogle Scholar
[21] Cheng, T.P., Mo, Z.Y. and Shao, J.L., Accelerating groundwater flow simulation in MODFLOW using JASMIN-based parallel computing, Groundwater 52, 194–205 (2014).Google Scholar
[22] Zhang, A.Q., Mo, Z.Y. and Yang, Z., Three-level hierarchical software architecture for data-driven parallel computing with applications, J. Comput. Res. Dev. 51, 2538–2546 (2014).Google Scholar
[23] Xu, X.W., Mo, Z.Y., Liu, Q.K. and An, H.B., An implicit time-integration algorithm for diffusion equations with structured AMR and applications, Chin. J. Comput. Phys. 29, 684–692 (2012).Google Scholar
[24] Shu, S., Yue, X.Q., Zhou, Z.Y. and Xu, X.W., Approximation and two-level algorithm of finite volume schemes for diffusion equations with structured AMR, Chin. J. Comput. Phys. 31, 390–402 (2014).Google Scholar
[25] Henson, V.E. and Yang, U.M., BoomerAMG: A parallel algebraic multigrid solver and preconditioner, Appl. Numer. Math. 41, 155–177 (2002).Google Scholar
[26] Berger, M.J. and Oliger, J., Adaptive mesh refinement for hyperbolic partial differential equations, J. Comput. Phys. 53, 484–512 (1984).Google Scholar
[27] Berger, M.J. and Colella, P., Local adaptive mesh refinement for shock hydrodynamics, J. Comput. Phys. 82, 64–84 (1989).CrossRefGoogle Scholar
[28] Gibbs, N.E., Poole, W.G. and Stockmeyer, P. K., An algorithm for reducing the bandwidth and profile of a sparse matrix, SIAM J. Numer. Anal. 13, 236–250 (1976).Google Scholar
[29] George, A. and Liu, J.W.H., The evolution of the minimum degree ordering algorithm, SIAM Rev. 31, 1–19 (1989).Google Scholar
[30] George, A., Nested dissection of a regular finite element mesh, SIAM J. Numer. Anal. 10, 345–363 (1973).CrossRefGoogle Scholar
[31] Saad, Y. and Suchomel, B., ARMS: An algebraic recursive multilevel solver for general sparse linear systems, Numer. Linear Algebra Appl. 9, 359–378 (2002).Google Scholar
[32] Osei-Kuffuor, D., Li, R.P. and Saad, Y., Matrix reordering using multilevel graph coarsening for ILU preconditioning, SIAM J. Sci. Comput. 37, A391–A419 (2015).Google Scholar
[33] Saad, Y., ILUT: A dual threshold incomplete ILU factorization, Numer. Linear Algebra Appl. 1, 387–402 (1994).Google Scholar