No CrossRef data available.
Article contents
XXV.—On Bipartite Functions
Published online by Cambridge University Press: 06 July 2012
Extract
If a row of n elements be taken, and closely following this array, but separated by a bar from it, we write n rows of n elements each; and closely following either outside column of this square array, but separated by a bar from it, we write n columns of n elements each; and closely following an outside row of this second square array, but separated by a bar from it, we write n rows of n elements each; and so on, passing from the rows or columns of one array to the columns or rows of the next, and ending not with a square array, but, as we began, with a single line of elements, we have the matrix representation of a bipartite function.
- Type
- Research Article
- Information
- Earth and Environmental Science Transactions of The Royal Society of Edinburgh , Volume 32 , Issue 3 , February 1886 , pp. 461 - 482
- Copyright
- Copyright © Royal Society of Edinburgh 1886
References
page 481 note * After the theory of this new class of functions had heen worked out under a temporary designation of my own, I got the Philosophical Transactions for 1858, in consequence of a communication on another matter from Professor Tait, in order to read Professor Cayley's Memoir on Matrices; and there found, immediately following the said memoir, another, “On the Automorphic Linear Transformation of a Bipartite Quadric Function.” This quadric function I saw at the first glance was a member of the class I had been dealing with—viz., that of the third degree. This led me to discard the name I had been employing, and to adopt bipartite instead. Professor Cayley gives the above extension of the theorem regarding the invariance of the discriminant of a quadric, but without proof, and not as if looking at it from that point of view. I think, however, I am correct in saying that this is the only point in which my paper has heen anticipated. Professor Cayley's notation for the bipartite we have used above is
which does not, I think, bear on the face of it the exact nature of the two-sidedness of a bipartite of the third degree; that is to say, it does not imply, as

does, that the function is equal to
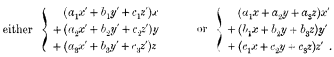
It may be of interest, as another evidence of the usefulness of bipartites, to remark here that the “Memoir on Matrices” came opportunely for another reason. The new instrument I had got hold of seemed as if specially devised for dealing with matrices, and I immediately succeeded in proving Cayley's great theorem that, if M be a matrix, the equation—
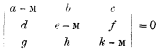
is satisfied by
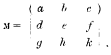
This proof, with its accessories, has been communicated to the Mathematical Society of London.


