No CrossRef data available.
Article contents
XIII.—The General Form of the Involutive 1-1 Quadric Transformation in a Plane
Published online by Cambridge University Press: 06 July 2012
Extract
§ 1. In a communication read before the Society, 3rd December 1900, Dr Muir discusses the generalisation, for more than two pairs of variables, of the proposition that: If
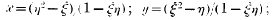
then
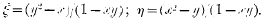
If we interpret (x, y) and (ξ, η) iis points in a plane, it is manifest that the transformation thereby obtained is a Cremona transformation. It has the special property of being reciprocal or involutive in character; i.e., if the point P is transformed into Q, then the repetition of the same transformation on Q transforms Q into P. Symbolically, if the transformation is denoted by T. T(P) = Q, and T(Q) = T2(P) = P; so that T2 = 1, and T = T−1. Moreover, if the locus of P (x, y) is a straight line, the locus of Q (ξ, η) is in general a conic.
- Type
- Research Article
- Information
- Earth and Environmental Science Transactions of The Royal Society of Edinburgh , Volume 40 , Issue 2 , 1905 , pp. 253 - 262
- Copyright
- Copyright © Royal Society of Edinburgh 1905


