Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T00:18:02.813Z Has data issue: false hasContentIssue false
  • English
  • Français

XXII.—An Attempt to Elucidate and Apply the Principles of Goniometry, as published by Mr Warren in his Treatise on the Square Roots of Negative Quantities

Published online by Cambridge University Press:  17 January 2013

Terrot
Get access Rights & Permissions [Opens in a new window]

Abstract

1. The symbol 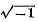is called an impossible or imaginary quantity, because, in analogy with the received laws of algebraic symbolism, it must mean such a quantity as, being multiplied into itself, gives for a product –1. Assuming, then, that every quantity must be either plus or minus, it follows that the square of every real quantity must be plus; and hence 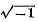, which gives its square minus, is called an imaginary or impossible quantity.

Type
Research Article
Information
Earth and Environmental Science Transactions of The Royal Society of Edinburgh , Volume 16 , Issue 3 , 1847 , pp. 345 - 355
Copyright
Copyright © Royal Society of Edinburgh 1847

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 348 note * This appears to be the view taken by Sir W. Hamilton, in the first of his series of papers on Symbolical Geometry, printed in the Cambridge and Dublin Mathematical Journal. He there says, “This symbolic sum of lines represents the total (or final) effect of all those successive rectilineal motions, or translations in space, which are represented by the several summands.”