1 Introduction
Current design research frequently draws conclusions based on small-scale behavioral experiments. Though valuable, these studies are severely limited in scope, and the results are difficult to generalize. The future of design cognition analysis will increasingly need to leverage computational methods for modeling and analyzing both individual and team behavior to enable larger scale studies. In addition, design cognition research must continue its trend toward more rigorous modeling of individual cognitive differences among designers to support more accurate simulations; cognitive style, or one’s preference for managing structure in solving problems, is one key example. In general, cognitive style describes patterns in problem-solving behavior and social interactions that result from an individual’s unique cognitive processes. For example, one measure of cognitive style differentiates verbal and visual learners (Riding Reference Riding1997), while another distinguishes more adaptive and more innovative thinkers (Kirton Reference Kirton2003). Cognitive style varies widely across engineers and designers, and differences in cognitive style can have positive or negative effects on the problem-solving performance of an individual or team (Kirton Reference Kirton2003; Jablokow Reference Jablokow2008; Jablokow et al. Reference Jablokow, Teerlink, Yilmaz, Daly and Silk2015b ; Sonalkar et al. Reference Sonalkar, Jablokow, Edelman, Mabogunje and Leifer2017). While researchers are beginning to develop simulation approaches for studying team problem solving, current methods do not yet attempt to model the influence of cognitive style on individual and team activities. To address this gap, we present in this paper an agent-based model for assessing how individuals’ cognitive styles impact an engineering team’s problem-solving performance, thereby linking cognition, behavior, and design activity.
Cognitive style is assessed using psychometric instruments such as the Kirton Adaption–Innovation Inventory (KAI) (Kirton Reference Kirton1976). While there are many ways to measure cognitive differences between people, KAI has been broadly studied and shown to have wide-reaching effects on problem-solving behavior (Kirton Reference Kirton1976, Reference Kirton2003; Jablokow & Booth Reference Jablokow and Booth2006; Jablokow et al. Reference Jablokow, Teerlink, Yilmaz, Daly and Silk2015b ,Reference Jablokow, Defranco, Richmond, Piovoso and Bilén a ; Sonalkar et al. Reference Sonalkar, Jablokow, Edelman, Mabogunje and Leifer2017). Therefore, although it is only one construct for explaining cognitive differences, KAI offers great potential for this vein of research. The KAI inventory measures an individual’s relative preference for structure along a bipolar continuum between two equally valued extremes (highly adaptive and highly innovative, respectively). More adaptive individuals prefer more structure in their problem solving (with more of it consensually agreed) and therefore tend to make incremental improvements within the current system to improve and enhance it. In contrast, more innovative individuals prefer less structure, with less concern about consensus, and tend to make radical changes that may ignore rules in an attempt to make the current system work “differently”; their efforts may or may not lead to improvements in that system. The Kirton A-I cognitive style influences both individual problem-solving characteristics and team interactions, and its effects have been studied in observations of engineering teams (Jablokow & Booth Reference Jablokow and Booth2006; Jablokow et al. Reference Jablokow, Teerlink, Yilmaz, Daly and Silk2015b ,Reference Jablokow, Defranco, Richmond, Piovoso and Bilén a ; Sonalkar et al. Reference Sonalkar, Jablokow, Edelman, Mabogunje and Leifer2017). However, it is unclear how cognitive style as measured by KAI could be used to inform the formation of engineering teams.
In fast moving projects, team formation is a critical task that managers must perform using their best guesses about optimal team composition and structure (Levitt Reference Levitt2012). As engineering teams become more interdisciplinary and develop increasingly complex structures, selecting the right members for a team is becoming more difficult as well (Crowder et al. Reference Crowder, Robinson, Hughes and Sim2012). However, research on optimal team formation strategies is limited. Research on collaboration in team performance is often based on qualitative descriptions and small studies (Bergner et al. Reference Bergner, Andrews, Zhu and Gonzales2016). In vivo studies of design teams over long periods of time are expensive, and the results are often applicable only in a specific context (Perisic et al. Reference Perisic, Martinec, Storga, Kanduc, Perišić, Martinec, Štorga and Kanduč2016).
In light of these issues, agent-based models of team problem solving can serve as a powerful tool for design cognition analysis, because they can quickly compare many different team compositions, structures, and processes (Crowder et al. Reference Crowder, Robinson, Hughes and Sim2012). Also, simulation can be useful for isolating independent variables in studies of cognition or social interaction (Singh, Dong & Gero Reference Singh, Dong and Gero2013), which is difficult in a human-subjects study. Current methods in design cognition analysis can simulate team problem solving involving agent communication (Fan & Yen Reference Fan and Yen2004; Perisic et al. Reference Perisic, Martinec, Storga, Kanduc, Perišić, Martinec, Štorga and Kanduč2016), sometimes with learning mechanisms (McComb, Cagan & Kotovsky Reference McComb, Cagan and Kotovsky2015; Hulse et al. Reference Hulse, Gigous, Tumer, Hoyle and Tumer2017) and social interaction (Tsvetovat & Carley Reference Tsvetovat and Carley2004; Singh et al. Reference Singh, Dong and Gero2013), and for some real-world design problems (Levitt Reference Levitt2012; Zurita et al. Reference Zurita, Colby, Tumer, Hoyle and Tumer2017). However, none of these methods address the role of cognitive style in problem solving and team performance explicitly.
This paper presents the KAI agent-based organizational optimization model (KABOOM), the first agent-based modeling framework for studying the problem-solving performance of teams of individuals with diverse cognitive styles. In KABOOM, individual agents exploring a solution space in order to maximize an objective are used to model human problem solving. Each agent has a unique cognitive style to reflect the range of styles measured by the KAI. An agent’s cognitive style influences its exploration and evaluation of the solution space. The interaction and collaboration between agents also depends on the agents’ respective cognitive styles. The goals of this research are: (1) to construct an agent-based model with agents that reflect the diverse cognitive styles of humans across the adaption–innovation spectrum; (2) using the model, analyze the performance of individual agents and teams solving a design problem; and (3) investigate how cognitive style impacts the effects of team specialization and communication on performance. As with any model, the assumptions made here limit the extent to which the model reflects real-world scenarios. Rather than predicting a specific team’s performance on a real-world problem, the end goal of this model is to investigate and understand the relationships between cognitive style and various aspects of team process (such as communication) and structure (such as specialization). Two outcomes of this research are: (1) hypotheses about cognitive style that can be investigated in human-subjects studies; and (2) heuristics related to cognitive style and team work that can support effective team management. After reviewing related work in adaption–innovation theory and agent-based modeling, this paper describes the development of KABOOM and discusses the results of several computational experiments on team specialization, communication, and cognitive style composition.
2 Background
2.1 The Kirton adaption-innovation inventory
The KAI is a psychometric instrument designed to measure a person’s cognitive style on a continuous spectrum that ranges from “highly adaptive” to “highly innovative” (Kirton Reference Kirton2003). In general terms, more adaptive problem solvers aim to do things better by using incremental changes to continuously improve a system or solution. In contrast, more innovative problem solvers prefer to do things differently, pursuing radically different solutions with more regard for originality than quality. Innovators tend to challenge the existing structures and constraints of a problem, while adaptors tend to support and stay within preexisting structures and bounds.
No cognitive style is universally better than another. However, one cognitive style is sometimes advantageous over others for a specific design problem. For example, problems that require adherence to a given structure, meticulous attention to detail, and conformance to specific rules or standards (e.g., repairing an antique grandfather clock, tuning a nuclear reactor) will tend to favor a more adaptive approach, although more innovative methods will still yield some kind of solution. In contrast, problems that require spanning multiple disciplines, taking a systems view, and challenging current practice (e.g., creating a disruptive product, “breaking” a patent) will tend to favor a more innovative approach, although more adaptive methods will still lead to some kind of progress.
The KAI has 32 items, each answered on a 5-point scale (Kirton Reference Kirton1976). In addition to an overall KAI score, the instrument provides three sub-scores: sufficiency of originality (SO), efficiency (E), and rule/group conformity (RG) (Kirton Reference Kirton1976) that are related to different aspects of cognitive style. The SO sub-score relates to the quantity and paradigm-relatedness of the solutions a person generates. More adaptive individuals tend to generate fewer ideas (based on cognitive preference, not ability); these ideas tend to be paradigm-preserving and are easier to integrate into existing systems. More innovative individuals tend to generate a higher number of solutions (again, based on preference, not capacity); these ideas tend to be more paradigm-breaking and can be difficult or even harmful to integrate into the existing system (Kirton Reference Kirton1976). The efficiency sub-score describes an individual’s attention to detail and methodological approach. More adaptive individuals prefer incremental changes to a solution that are sure to improve quality. In contrast, more innovative individuals may alter a solution in riskier, less well-defined ways, with less regard for the resulting quality (Kirton Reference Kirton1976). The RG sub-score describes an individual’s preference for adhering to constraints and norms, as well as their cohesion with a group (i.e., social structure). More adaptive individuals prefer to leverage the prevailing rules, guidelines, and norms in their problem solving; they also tend to promote group cohesion and continuity. More innovative individuals, however, are more likely to disregard the prevailing rules and norms, and are less concerned about conforming to a group; they may actively move away from group consensus and can cause disruption or discord in a team (Kirton Reference Kirton1976). The methods section describes how each of these sub-factors of KAI inform the development of agents that have their own cognitive styles.
2.2 Cognitive style diversity and design teams
When individuals work together, their diverse cognitive characteristics can influence their collaborations in both positive and negative ways. Kirton uses the term cognitive gap to describe differences in cognitive level (intelligence, experience, knowledge, etc.) and/or cognitive style that can appear between two individuals, an individual and a group, two groups, or between an individual/group and the problem at hand (Kirton Reference Kirton2003; Jablokow & Booth Reference Jablokow and Booth2006). In previous work related to KAI and teams, Kurtzberg (Reference Kurtzberg2005) studied the creative fluency of homogeneous teams and heterogeneous teams (as categorized by KAI cognitive gaps) and found that heterogeneous teams outperformed homogeneous teams in terms of creative output (i.e., number of ideas). Hammerschmidt (Reference Hammerschmidt1996) studied team success and cognitive style diversity using KAI and found that teams had higher levels of success when tasks were coordinated with KAI (e.g., a more adaptive task aligned with a more adaptive sub-team). His work also revealed that when sub-teams had similar KAI scores (i.e., were homogeneous), overall team success increased as a result of enhanced inter-team communication, while diverse (i.e., heterogeneous) teams were more likely to fail as a result of unresolved cognitive gaps. Jablokow et al. (Reference Jablokow, Teerlink, Yilmaz, Daly and Silk2015b ) explored the effects of cognitive gaps on dyad performance and interactions between design team members during concept generation. Their results suggest that as the cognitive gap between team members increases, the more adaptive team member tends to feel that they contributed less to team ideation, while the more innovative team member tends to feel that they contributed more. In other previous work by Jablokow et al. (Reference Jablokow, Teerlink, Yilmaz, Daly and Silk2015b ), the results suggest that the presence of more innovative individuals on a team may be correlated with a greater occurrence of unique ideas in the team, where “unique” was defined as “new to the current team discussion”. They also found that more innovative teams (determined by KAI mean) tended to exhibit team interactions with a higher degree of integration between topics.
2.3 Mechanisms of agent-based modeling for design teams
An agent-based model (sometimes called a multi-agent system) is a software simulation method in which autonomous, heterogeneous agents interact with their environment and other agents (Garcia Reference Garcia2005). Each agent acts with a set of behavioral rules in order to accomplish an objective (Bonabeau Reference Bonabeau2002). Rather than defining the macroscopic behavior of a system, an agent-based model only defines behavioral rules for individual agents and a structure for agent interactions (Jennings Reference Jennings2000; Bonabeau Reference Bonabeau2002). Agents make run-time decisions based on limited knowledge of the environment and limited decision-making capabilities (Jennings Reference Jennings2000; Tsvetovat & Carley Reference Tsvetovat and Carley2004). In addition to these cognitive constraints, agents may be socially constrained with limited ability to connect and share information with other agents (Tsvetovat & Carley Reference Tsvetovat and Carley2004). By simulating agent interactions, an agent-based model can capture emergent phenomena that are more than the sum of the individual agents’ actions (Bonabeau Reference Bonabeau2002).
Some studies investigate the frequency of communication among agents throughout the course of the problem-solving period. In the context of design research, communication refers to the exchange of design solutions (Singh et al. Reference Singh, Dong and Gero2013). A solution is the outcome of a design effort, which, when communicated to a teammate, may prove either beneficial or detrimental in the form of false leads, failures, or flawed concepts. Research on communication in design teams shows that more communication is not necessarily better; there is a trade-off between communication frequency and individual work (Patrashkova-Volzdoska et al. Reference Patrashkova-Volzdoska, McComb, Green and Dale Compton2003; Patrashkova & McComb Reference Patrashkova and McComb2004). Some researchers have shown that intermittent communication can provide the benefits of constant communication, as well as the benefits of individual work (Bernstein, Shore & Lazer Reference Bernstein, Shore and Lazer2018). There are even some cases where no communication is the best team process strategy (McComb, Cagan & Kotovsky Reference McComb, Cagan and Kotovsky2017a ; McComb & Maier Reference McComb and Maier2018).
Engineering teams often divide the design of complex systems into multiple components that are then addressed or solved by specialized team members with corresponding expertise in a specific domain (Hulse et al. Reference Hulse, Gigous, Tumer, Hoyle and Tumer2017, Reference Hulse, Tumer, Hoyle and Tumer2018). This multi-component approach to complex systems design is analogous to coordination between multiple agents in a computational model: decisions are made with respect to separate components and later aggregated to form a global solution (Zurita et al. Reference Zurita, Colby, Tumer, Hoyle and Tumer2017). An agent-based model can reflect the way engineering teams solve complex systems in a distributed manner by assigning agents to specialized sub-teams that each control a subset of all design variables for a global objective function (Hulse et al. Reference Hulse, Tumer, Hoyle and Tumer2018). This approach makes it possible to use an agent-based model to rapidly investigate the effects of team structure on a design team’s performance.
Appropriate team composition is critical for high team performance (Martínez-Miranda & Pavón Reference Martínez-Miranda and Pavón2012) and should consider not only the personal traits of individuals, but also the nature of the problem being addressed by the team (Zhang et al. Reference Zhang, Luo, Yang, Li, Schlick and Grandt2009). Team composition can have a detrimental effect on performance and social interactions if teams are not carefully constructed and managed (Martínez-Miranda & Pavón Reference Martínez-Miranda and Pavón2012). Although this paper examines team composition in terms of the cognitive styles of agents on a team, other factors of team composition exist and have been studied both in human-subjects studies and through computational modeling. According to Singh et al. (Reference Singh, Dong and Gero2013), a team’s composition refers to its size, life-span (one project or several), location (collocated or geographically distributed), structure (flat or hierarchical), and heterogeneity (homogeneous or heterogeneous). Not surprisingly, a team’s composition in terms of domain of expertise also plays a key part in product development success (Brown & Eisenhardt Reference Brown and Eisenhardt1995). However, there is little evidence regarding how other personal cognitive qualities like cognitive style influence a team’s success. Martínez-Miranda & Pavón (Reference Martínez-Miranda and Pavón2012) state that although some human resource departments use tests of personality and cognitive level:
It could be even more useful for project managers to apply the results of cognitive and psychological tests to build virtual teams and simulate their possible behaviors in order to analyze what could happen when people with specific characteristics interact with each other and with their respective tasks over the entire duration of a project. (Martínez-Miranda & Pavón Reference Martínez-Miranda and Pavón2012)
Among the large number of psychological instruments used today, many have limited validation or scientific support. The KAI, however, has been extensively validated and is regularly used for team management (Kirton Reference Kirton2003). This research, therefore, aims to fill a gap at the intersection of cognitive style and agent-based modeling by incorporating the Kirton Adaption-Innovation cognitive style characteristics into an agent-based model of engineering teamwork.
2.4 State of the art
In the 1990s, managers of the semiconductor manufacturer “Micro” were faced with the challenge of developing high-performance teams for complex and concurrent projects on an extremely rapid product life cycle (Levitt Reference Levitt2012). While the performance of their semiconductor chips could be modeled with computer simulations, managers still used guess-and-check methods for the design of their teams – but they began to ask for computational tools that could simulate team performance in the same way that software simulations could predict the performance of an engineering design (Levitt Reference Levitt2012). This led to the virtual design team (VDT) project (Kunz et al. Reference Kunz, Christiansen, Cohen, Jin and Levitt1998; Levitt Reference Levitt2012), an early effort to create simulation tools that helped managers design software teams by simulating the assignment and completion of work items. The VDT simulation divides a problem into tasks and types of work, and then uses stochastic discrete-event simulation to model the time and number of errors incurred in completing each task. VDT models real and complex projects, and includes both errors in task completion and noise in communication (Levitt Reference Levitt2012).
Since then, many researchers have developed models with the aim of reflecting some aspect of human behavior or teamwork (Vermillion & Malak Reference Vermillion and Malak2015; Fernandes et al. Reference Fernandes, Henriques, Silva and Pimentel2017; Vermillion & Malak Reference Vermillion and Malak2018) more accurately. These models vary in their purpose. Some, like VDT, are team management simulation tools that model team performance to avoid the associated costs of long and expensive human-subjects studies (Perisic et al. Reference Perisic, Martinec, Storga, Kanduc, Perišić, Martinec, Štorga and Kanduč2016). Other models focus on studying the social aspects of communication and collaboration (Tsvetovat & Carley Reference Tsvetovat and Carley2004; Singh et al. Reference Singh, Dong and Gero2013). For example, Tsvetovat & Carley (Reference Tsvetovat and Carley2004) develop a detailed model of complex social and technological systems by including learning, social network theory, and social psychology in an agent-based model. Recent research in systems engineering by Vermillion and Malak uses agent-based approaches to investigate the delegation of authority and use of incentives in design teams (Vermillion & Malak Reference Vermillion and Malak2015, Reference Vermillion and Malak2018). Fan & Yen (Reference Fan and Yen2004) present an extensive review of agent-based models addressing communication and collaboration; some of the models reviewed include emotion and sentiment (Fan & Yen Reference Fan and Yen2004). However, the authors are not aware of any models that incorporate individual cognitive style for heterogeneous agents.
Recently, several agent-based models have attempted to focus on the personalities, attitudes, and emotions of problem solvers, as well as their knowledge (Martinez-Miranda et al. Reference Martinez-Miranda, Aldea, Bañares-Alcantara and Alvarado2006; Zhang et al. Reference Zhang, Luo, Yang, Li, Schlick and Grandt2009; Dehkordi, Thompson & Larsson Reference Dehkordi, Thompson and Larsson2012). For example, the TEAKS framework (Martinez-Miranda et al. Reference Martinez-Miranda, Aldea, Bañares-Alcantara and Alvarado2006; Martínez-Miranda & Pavón Reference Martínez-Miranda and Pavón2012) models the social and emotional aspects of team problem solving. Agent interactions are based on the PECS (physics, emotion, cognition, and social status) framework (Urban & Schmidt Reference Urban and Schmidt2001), and personality is described by drive, influence, steadiness, and compliance. Dehkordi et al. (Reference Dehkordi, Thompson and Larsson2012) study work-overload impact by modeling the effects of stress and motivation on team performance, and Zhang et al. (Reference Zhang, Luo, Yang, Li, Schlick and Grandt2009) present a model where human behavior, development process, and organizational structure all influence design outcomes. These models focus on emotions and sentiments to elicit human-like behaviors in computational agents.
Finally, some models implement contextualized, real-world design problems that are solved by teams of agents in an agent-based model (McComb et al. Reference McComb, Cagan and Kotovsky2015; Zurita et al. Reference Zurita, Colby, Tumer, Hoyle and Tumer2017). Work by Zurita et al. (Reference Zurita, Colby, Tumer, Hoyle and Tumer2017) is an example of an agent-based model specifically created for a contextualized problem: designing a formula SAE racing vehicle. Their model demonstrates that by using a cooperative evolutionary algorithm, an agent-based model can design a complex system. Like Hulse et al. (Reference Hulse, Tumer, Hoyle and Tumer2018), members of the design team adopt specializations by breaking the problem into separate functional sub-systems (e.g., engine, suspension, and brakes).
The CISAT framework (McComb et al. Reference McComb, Cagan and Kotovsky2015, Reference McComb, Cagan and Kotovsky2017a ; McComb, Cagan & Kotovsky Reference McComb, Cagan and Kotovsky2017b ) is another agent-based model that uses contextualized problems to study how problem characteristics affect the optimal team process and team characteristics. The CISAT framework reflects eight characteristics of both team activity and individual cognition, namely: organic interaction timing, quality-informed solution sharing, quality bias reduction, self-bias, operational learning, breadth versus depth solution search, and satisficing (McComb et al. Reference McComb, Cagan and Kotovsky2015). In McComb et al. (Reference McComb, Cagan and Kotovsky2017a ), the CISAT model is used to find optimal team characteristics based on properties of the problem being addressed. These two models provide much of the inspiration for KABOOM.
3 Methods
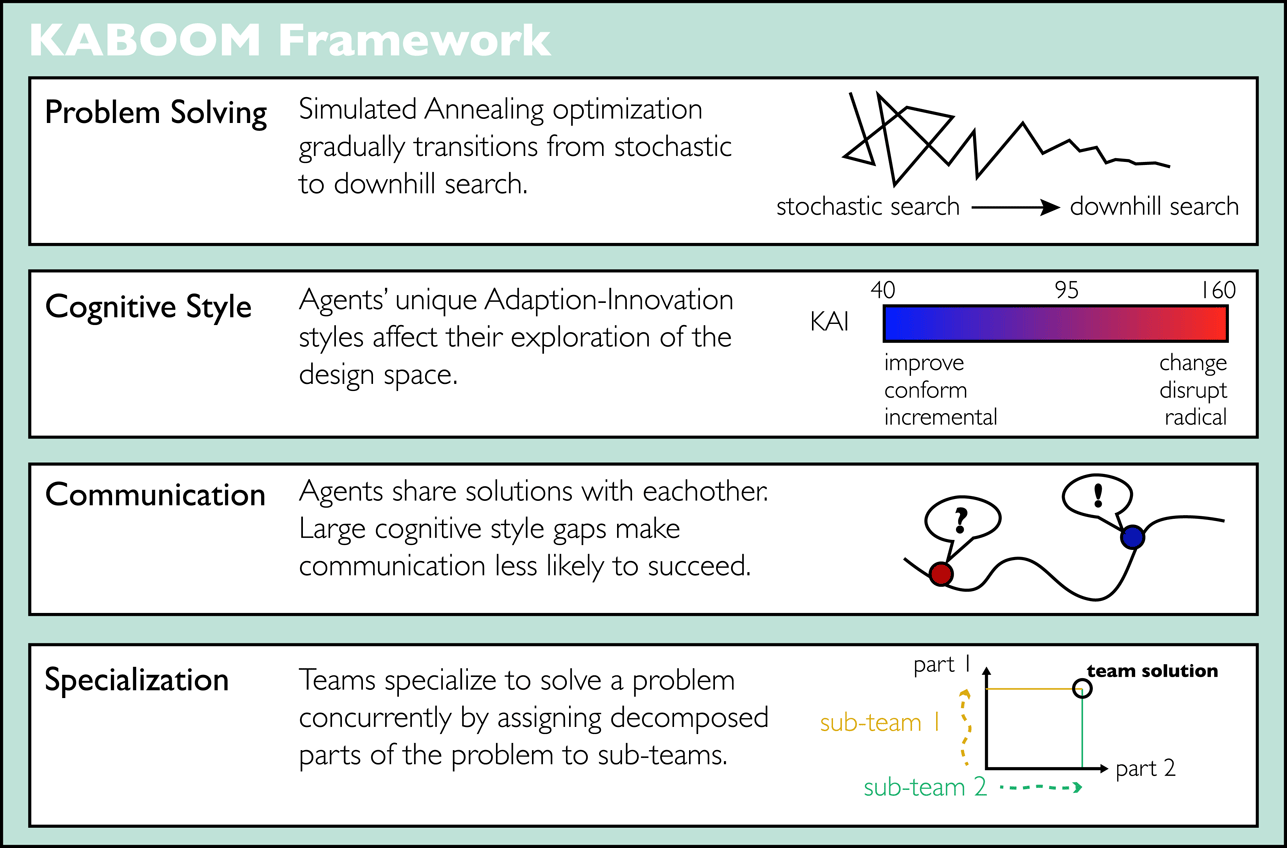
KABOOM is the first agent-based model to incorporate cognitive style of heterogeneous agents as a strategy to simulate the problem-solving behaviors of human teams. This section describes: (1) the agent-based model framework for KABOOM; (2) the implementation of the Kirton Adaption-Innovation cognitive style for agents; (3) communication in the model through pairwise solution sharing and team meetings; and (4) creating a virtual population with KAI cognitive style traits. Figure 1 provides a high-level summary of the key components of the model.
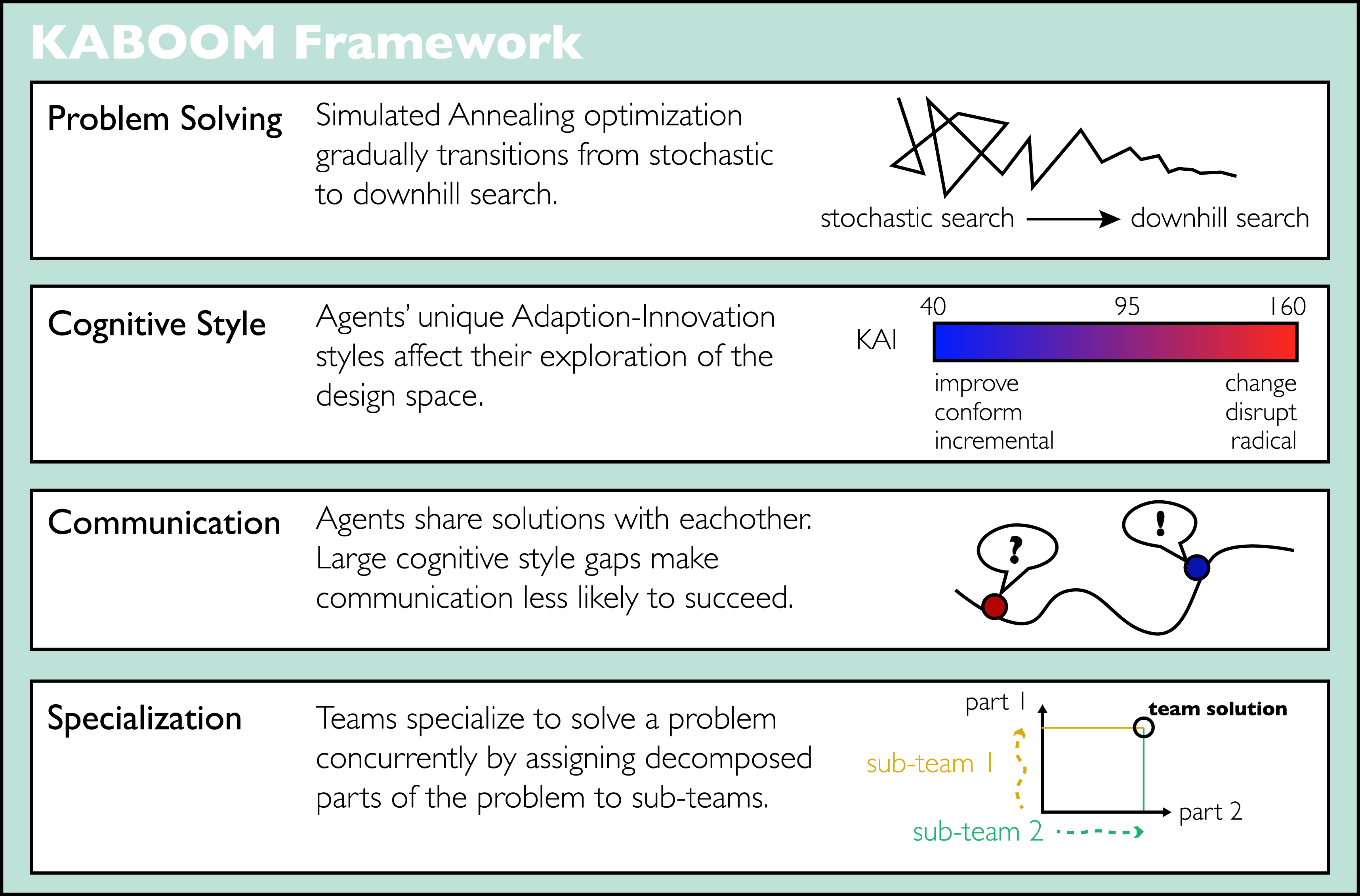
Figure 1. Outline of the KABOOM framework and its key features.
3.1 The KABOOM framework
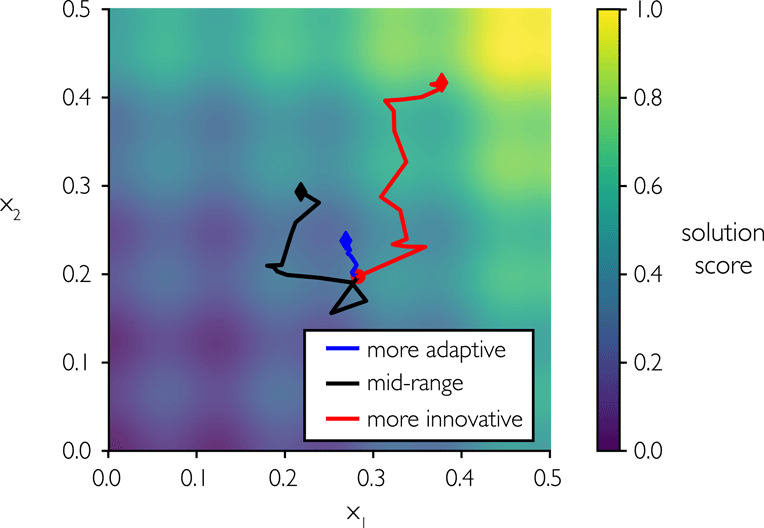
The KABOOM is a multi-agent optimization scheme in which independent software agents explore a solution space by varying parameters and evaluating a cost function. KABOOM is based on a simulated-annealing (Kirkpatrick, Gelatt & Vecchi Reference Kirkpatrick, Gelatt and Vecchi1983) optimization algorithm: the agents start with a high “temperature”, allowing them to explore widespread solutions non-greedily; the temperature gradually cools over the course of the simulation, leading to a local and more greedy search. The gradual transition from stochastic to downhill search in simulating annealing reflects the nature of human problem solving (Cagan & Kotovsky Reference Cagan and Kotovsky1997; Yu et al. Reference Yu, Honda, Sharqawy and Yang2016) and has been used in other human problem-solving simulations (McComb et al. Reference McComb, Cagan and Kotovsky2015). Figure 2 illustrates an agent problem solving in a simulated-annealing framework. The agent explores a 2-dimensional problem space with the goal of maximizing an objective function (left). The black line connects the sequence of solutions explored by the agent over the course of 100 iterations of the simulation, ending at the black diamond. The agent makes large changes to the solution early on, followed by smaller steps toward the end, in accordance with the simulated-annealing scheme.

Figure 2. Simulated annealing involves agents exploring a solution space (right) in order to maximize a defined objective function (left). The path on the right shows a series of solutions starting at the circle and ending at the diamond.
In this paper, a solution is a set of parameters that define a position in the solution space, and the quality of a solution is the value of the objective function for those parameters. Team performance is taken to be the best solution any individual on a team has found. While this approach is the norm in the optimization and modeling literature, future work could consider more subtle measures of performance that include social integrity of the team, self-efficacy, consumption of resources such as money and time, or other measures of performance.
Many computational models of team problem solving assume that agents can perfectly evaluate the objective function for solutions they create. This is due in part to agent-based models being grounded in the optimization literature. In contrast, KABOOM assumes agents can evaluate the quality of their solutions using the objective function, but their perception of solution quality is affected by their respective cognitive styles. Each agent has an assigned cognitive style, which includes the three sub-score dimensions of sufficiency of originality (SO), efficiency (E), and rule/group conformity (RG), in addition to the total score (KAI). These parameters influence how the agent perceives solution quality and how it explores the solution space. The following sections describe how the total KAI score and each sub-score impact agent behavior.
3.1.1 Simulating cognitive style
The agents’ exploration of the solution space depends on their total KAI score, as well as the three sub-factor scores of sufficiency of originality (SO), efficiency (E), and rule/group conformity (RG). People with higher KAI scores tend to make larger changes to a design in search of a different solution, while people with lower KAI scores tend to make smaller changes to refine an existing solution. In the simulation, the distance an agent moves in the solution space on one turn (iteration) is positively correlated with the total KAI score. Figure 3 illustrates the differences in step size for agents of adaptive, mid-range, and innovative styles in a 2-dimensional problem. When searching for new solutions, a more adaptive agent moves in smaller, incremental steps, tweaking the solution with marginal adjustments. In contrast, a more innovative agent moves in larger leaps, often generating ideas that are distant and very distinct from their current solution.

Figure 3. Agents with more adaptive styles (lower KAI scores) move in smaller steps on each iteration, while agents with more innovative styles (higher KAI scores) take larger steps in the solution space.
Each agent has an individual speed parameter with an initial value dependent on their total KAI score. Speed determines how closely or distantly related an agent’s subsequent solutions are. Speed is roughly analogous to novelty of solutions in real-world problems, in that high speed will lead to a series of very distinct solutions, while low speed will lead to a series of very similar solutions. The speed decays geometrically throughout the course of the simulation. The distance,
![]() $D$
, from the current solution to the next solution an agent generates is drawn from a chi (
$D$
, from the current solution to the next solution an agent generates is drawn from a chi (
![]() $\unicode[STIX]{x1D712}$
) distribution and scaled by the agent’s current speed,
$\unicode[STIX]{x1D712}$
) distribution and scaled by the agent’s current speed,
![]() $s$
:
$s$
:
where
![]() $\unicode[STIX]{x1D712}$
is a random variable characterized by the chi probability density function with
$\unicode[STIX]{x1D712}$
is a random variable characterized by the chi probability density function with
![]() $k=1.9$
degrees of freedom. The minimum travel distance in one step is set to one ten-thousandth of the entire space, and there is no upper bound. The agent’s start speed,
$k=1.9$
degrees of freedom. The minimum travel distance in one step is set to one ten-thousandth of the entire space, and there is no upper bound. The agent’s start speed,
![]() $s_{0}$
, is calculated as
$s_{0}$
, is calculated as
where
![]() $KAI^{\ast }$
is the standardized KAI score (re-scaled for a mean of 0 and a standard deviation of 1),
$KAI^{\ast }$
is the standardized KAI score (re-scaled for a mean of 0 and a standard deviation of 1),
![]() $\unicode[STIX]{x1D707}_{s}$
is the average starting speed for all agents, and
$\unicode[STIX]{x1D707}_{s}$
is the average starting speed for all agents, and
![]() $\unicode[STIX]{x1D70E}_{s}$
is the standard deviation of starting speed across all agents.
$\unicode[STIX]{x1D70E}_{s}$
is the standard deviation of starting speed across all agents.
3.1.2 Model parameters
Parameters in the model are generally tuned to reflect observed human behavior. Except where noted, the parameters were held constant at the values listed in Table 1. An appendix contains a table listing all parameter values for each figure in the paper.
Table 1. List of model parameters and their default values

3.1.3 Efficiency
Efficiency describes an individual’s preference for structure in their working methods, which range from applying highly detailed and incremental improvements to a solution (more adaptive) to dramatically or tangentially altering a solution, with less regard for detail and quality (more innovative). The temperature parameter in simulated annealing determines the probability of an agent accepting a candidate solution that does not improve the objective function relative to their own current solution. In a real-world design setting, temperature corresponds to exploration. Early on in the design process, designers explore new solutions with little regard for quality in order to expand the known solution space. As the design process continues, solution quality becomes more important and exploration transitions to exploitation.
In KABOOM, an agent’s starting temperature is correlated with the E sub-score. Temperature always decreases geometrically over the course of the simulation, but both the start temperature
![]() $T_{0}$
and the cooling rate are a function of E. An agent with a higher (more innovative) E sub-score starts with a higher temperature, and thus a higher probability of accepting solutions that do not improve the objective function. This can cause them to leave good solutions behind and miss high-quality nearby solutions, but it can also allow them to escape local minima to find better solutions in a “rough” optimization topology. Agents with higher efficiency scores also cool down slower, meaning they might never reach a very low temperature or refine a single local solution. In contrast, an agent with a lower (more adaptive) E sub-score starts with a lower temperature, and thus a lower probability of accepting solutions that do not improve the objective function. This can cause them to quickly achieve locally optimal results, but it can also lead them to become stuck in local minima. The resulting behavior of the agents overall is that the more adaptive agents choose a solution early on and polish it to perfection, while the more innovative agents spend most of their time exploring very diverse solutions without refining them. The agent’s start temperature
$T_{0}$
and the cooling rate are a function of E. An agent with a higher (more innovative) E sub-score starts with a higher temperature, and thus a higher probability of accepting solutions that do not improve the objective function. This can cause them to leave good solutions behind and miss high-quality nearby solutions, but it can also allow them to escape local minima to find better solutions in a “rough” optimization topology. Agents with higher efficiency scores also cool down slower, meaning they might never reach a very low temperature or refine a single local solution. In contrast, an agent with a lower (more adaptive) E sub-score starts with a lower temperature, and thus a lower probability of accepting solutions that do not improve the objective function. This can cause them to quickly achieve locally optimal results, but it can also lead them to become stuck in local minima. The resulting behavior of the agents overall is that the more adaptive agents choose a solution early on and polish it to perfection, while the more innovative agents spend most of their time exploring very diverse solutions without refining them. The agent’s start temperature
![]() $T_{0}$
is calculated as
$T_{0}$
is calculated as
where
![]() $E^{\ast }$
is the standardized efficiency sub-score (re-scaled for a mean of 0 and a standard deviation of 1),
$E^{\ast }$
is the standardized efficiency sub-score (re-scaled for a mean of 0 and a standard deviation of 1),
![]() $\unicode[STIX]{x1D707}_{T}$
is the average temperature for all agents, and
$\unicode[STIX]{x1D707}_{T}$
is the average temperature for all agents, and
![]() $\unicode[STIX]{x1D70E}_{T}$
is the standard deviation of temperature across all agents.
$\unicode[STIX]{x1D70E}_{T}$
is the standard deviation of temperature across all agents.
The agent’s ratio of start temperature
![]() $r_{0}$
to final temperature
$r_{0}$
to final temperature
![]() $r_{f}$
is
$r_{f}$
is
which is bounded by
![]() $10^{-10}$
and 1. The geometric decay ratio for each time step is calculated based on start temperature, start-to-end ratio, and the number of steps in the simulation. Figure 4(A) shows the temperature over the course of a simulation for agents with more innovative (high E), mid-range (mid-range E), and more adaptive (low E) efficiency sub-scores. The agent’s speed decays with the same ratio as the temperature.
$10^{-10}$
and 1. The geometric decay ratio for each time step is calculated based on start temperature, start-to-end ratio, and the number of steps in the simulation. Figure 4(A) shows the temperature over the course of a simulation for agents with more innovative (high E), mid-range (mid-range E), and more adaptive (low E) efficiency sub-scores. The agent’s speed decays with the same ratio as the temperature.

Figure 4. (A) Cooling schedules for agents with different efficiency sub-scores. (B) In calculating the perceived memory location, an agent’s past memories are weighted based on the serial position effect reflected in this curve: the most recent memories and earliest memories are recalled more easily than intermediate memories.
In simulated annealing, the probability that an agent will accept or reject a solution that is inferior to its current solution depends on its temperature and the difference in solution quality according to Equation (5) (Kirkpatrick et al. Reference Kirkpatrick, Gelatt and Vecchi1983). At high temperatures, an agent will accept solutions regardless of quality, but at low temperatures, agents only accept solutions that improve the objective function, as shown below:
where
![]() $P_{\text{accept}}$
is the probability that an agent with current solution
$P_{\text{accept}}$
is the probability that an agent with current solution
![]() $\vec{x}$
accepts a new solution
$\vec{x}$
accepts a new solution
![]() $\vec{x}_{n}$
that does not improve the objective function
$\vec{x}_{n}$
that does not improve the objective function
![]() $f$
as a function of current temperature
$f$
as a function of current temperature
![]() $T$
and a constant
$T$
and a constant
![]() $k_{B}$
. We can absorb
$k_{B}$
. We can absorb
![]() $k_{B}$
into the calculation of temperature.
$k_{B}$
into the calculation of temperature.
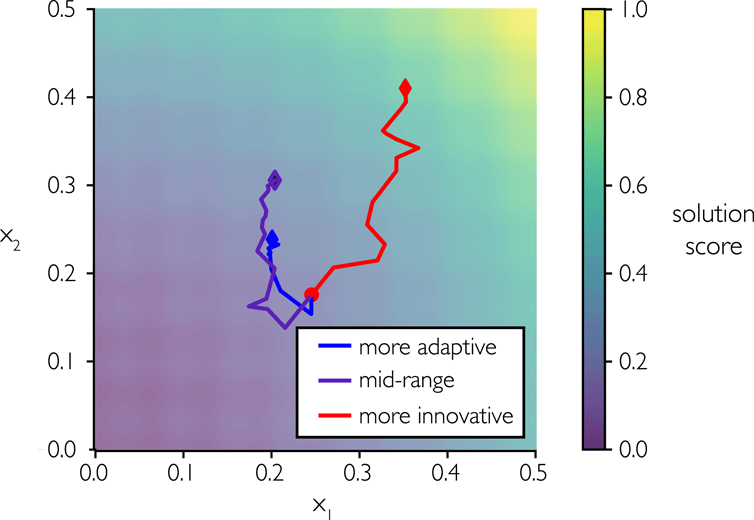
Figure 5 illustrates the effect of the efficiency style sub-factor on three agents’ exploration of the solution space. Compared to the mid-range agent (black), the more adaptive agent (blue) refines an early solution, while the more innovative agent (red) continuously explores without refining a solution.

Figure 5. Effect of E sub-factor on solution space exploration.
3.1.4 Sufficiency of originality
An agent’s desire to retain and modify known solutions or, conversely, to explore more unfamiliar ideas, is related to the SO sub-score of KAI. When agents evaluate a candidate solution in KABOOM, more adaptive agents are more likely to accept a candidate solution that directs them toward their previous solutions and are less likely to accept a solution that leads them away from previous solutions. On the other hand, more innovative agents prefer to choose ideas that move them further from ideas they have explored in the past and to reject ideas that lead them toward their previous solutions. An agent’s perception of its previous solutions is represented by a single point in the solution space, which is a weighted mean (centroid) of all of their previous positions or “memories”. The weights on an agent’s memories are strongest for the most recent memories, weakest for middle memories, and intermediate strength for the earliest memories (Figure 4(B)). This reflects the serial position effect (Colman Reference Colman2015), which describes how people tend to remember early memories (primacy effect) and recent memories (recency effect) more readily than intermediate memories.
The direction of the weighted memory position from the current position is a weighted average of the directions to all previous solutions the agent has visited. We call
![]() $\vec{v}_{\text{mem}}$
the perceived memory direction, where the weights are given by the primacy–recency bias function
$\vec{v}_{\text{mem}}$
the perceived memory direction, where the weights are given by the primacy–recency bias function
![]() $Q$
:
$Q$
:
and where the memory
![]() $\boldsymbol{M}$
is a list of
$\boldsymbol{M}$
is a list of
![]() $N$
previous solutions (each memory being a vector of the same shape as the current solution
$N$
previous solutions (each memory being a vector of the same shape as the current solution
![]() $\vec{x}$
). The primacy–recency bias function for memory
$\vec{x}$
). The primacy–recency bias function for memory
![]() $n$
of
$n$
of
![]() $N$
total memories is:
$N$
total memories is:
which gives a U-shaped curve with stronger biases for the earliest and most recent memories, respectively, than for other memories (Figure 4(B)). The weights are calculated with this equation then normalized so that they sum to 1.
The direction of the candidate solution from the current solution is the vector difference between the candidate solution and the current solution,
![]() $\vec{v}_{n}=\vec{x}_{n}-\vec{x}$
. The dot product of these two directions indicates whether the new solution is in the direction of the perceived memory or away from the perceived memory. We call this dot product the originality
$\vec{v}_{n}=\vec{x}_{n}-\vec{x}$
. The dot product of these two directions indicates whether the new solution is in the direction of the perceived memory or away from the perceived memory. We call this dot product the originality
![]() $\unicode[STIX]{x1D6FA}$
:
$\unicode[STIX]{x1D6FA}$
:
Then, the SO preference
![]() $P_{SO}$
is:
$P_{SO}$
is:
where
![]() $SO^{\ast }$
is the standardized SO score (re-scaled for a mean of 0 and a standard deviation of 1), and
$SO^{\ast }$
is the standardized SO score (re-scaled for a mean of 0 and a standard deviation of 1), and
![]() $W_{SO}$
is a global scaling constant that determines the strength of the SO preference. For this paper, we set
$W_{SO}$
is a global scaling constant that determines the strength of the SO preference. For this paper, we set
![]() $W_{SO}$
to 2, which creates a range of behaviors for agents across the KAI cognitive style spectrum. When an agent evaluates the quality of a candidate solution, the SO preference
$W_{SO}$
to 2, which creates a range of behaviors for agents across the KAI cognitive style spectrum. When an agent evaluates the quality of a candidate solution, the SO preference
![]() $P_{SO}$
and RG preference
$P_{SO}$
and RG preference
![]() $P_{RG}$
(explained below) influence the perceived solution quality: the preferences are added to the true value of the objective function for the candidate solution. In other words, the perceived solution quality
$P_{RG}$
(explained below) influence the perceived solution quality: the preferences are added to the true value of the objective function for the candidate solution. In other words, the perceived solution quality
![]() $f_{P}$
of a candidate solution
$f_{P}$
of a candidate solution
![]() $\vec{x}_{n}$
is related to the true solution quality
$\vec{x}_{n}$
is related to the true solution quality
![]() $f(\vec{x}_{n})$
by
$f(\vec{x}_{n})$
by
Figure 6 illustrates the effect of the SO cognitive style sub-factor on three agents’ exploration in a 2-dimensional solution space. The black line shows the solution path of an agent with a mid-range cognitive style. The red line shows the path of a more innovative agent in the same space, with only the SO preference active (and otherwise identical to the mid-range agent). The innovative SO style gives the agent a preference for solutions that move it away from its previous solutions, leading the agent to explore further into the corner of the solution space. On the other hand, the blue line shows the more adaptive agent’s preference for solutions that are close to its previous solutions, leading to a dense packing of solutions near its original starting point.

Figure 6. Effect of SO sub-factor on solution space exploration.
3.1.5 Rule/group conformity
The third cognitive style sub-score, rule/group conformity (RG), describes an individual’s preference for managing structure in both impersonal and personal contexts. More adaptive individuals prefer to leverage existing impersonal structures, such as rules, guidelines, and precedents, while more innovative individuals are more likely to bend or violate these structures. A similar pattern of behavior emerges for personal structures, such as groups or teams. A person with an adaptive RG style tends to cohere with the group and seek group consensus, while a more innovative person tends to diverge from and may even disrupt the group.
In order to capture one aspect of the RG sub-factor, the present model focuses on conformity to personal structures (i.e. an individual’s desire to converge or diverge from group consensus). Future work could develop other aspects of RG, for instance, by modifying the agents’ adherence to optimization constraints. In KABOOM, the more adaptive agents are more likely to move toward solutions that bring them closer to the team’s average position, thus encouraging group cohesion. More innovative agents, on the other hand, have a preference for solutions that move them away from the mean position of the group.
In KABOOM, this aspect of RG is implemented in a similar way to SO by replacing an agent’s memories with the current solutions. In other words, while SO makes agents favor solutions toward (more adaptive) or away from (more innovative) their own previous solutions, RG gives agents a preference toward (more adaptive) or away from (more innovative) the current solutions of their teammates (Figure 7).
A “team position”
![]() $\vec{x}_{\text{team}}$
is represented by the centroid of the current solution of each member of the team:
$\vec{x}_{\text{team}}$
is represented by the centroid of the current solution of each member of the team:
where
![]() $T$
is the team of
$T$
is the team of
![]() $N$
agents, and
$N$
agents, and
![]() $T_{n}$
selects the current solution of each agent on the team. As before, the direction of the candidate solution from the current solution is the vector difference,
$T_{n}$
selects the current solution of each agent on the team. As before, the direction of the candidate solution from the current solution is the vector difference,
![]() $\vec{v}_{n}=\vec{x}_{n}-\vec{x}$
. Likewise, the direction of the team position from the current position is
$\vec{v}_{n}=\vec{x}_{n}-\vec{x}$
. Likewise, the direction of the team position from the current position is
![]() $\vec{v}_{\text{team}}=\vec{x}_{\text{team}}-\vec{x}$
.
$\vec{v}_{\text{team}}=\vec{x}_{\text{team}}-\vec{x}$
.
The dot product of these two vectors indicates whether the new solution is in the direction of the team (positive dot product) or away from the team (negative dot product). We call this dot product the conformity
![]() $C$
:
$C$
:
Then, the group conformity preference
![]() $P_{RG}$
is:
$P_{RG}$
is:
where
![]() $RG\ast$
is the standardized RG sub-score (re-scaled for a mean of 0 and a standard deviation of 1), and
$RG\ast$
is the standardized RG sub-score (re-scaled for a mean of 0 and a standard deviation of 1), and
![]() $W_{RG}$
is a global constant used to change the strength of the RG preference, which is set to 2 to create a range of behaviors.
$W_{RG}$
is a global constant used to change the strength of the RG preference, which is set to 2 to create a range of behaviors.
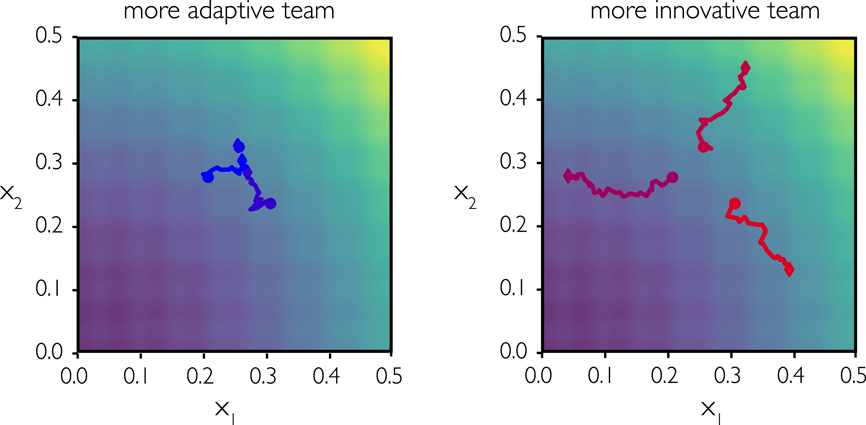
Figure 7 illustrates the effect of the RG cognitive style sub-factor for adaptive and innovative teams, respectively, of three agents each. Agents with a more adaptive RG style prefer solutions that bring them toward their team, resulting in team convergence (left), while more innovative agents seek solutions away from their team, leading to team divergence (right).

Figure 7. Effect of RG sub-factor on homogeneous teams of adaptive style and innovative style, respectively (blue paths show adaptive agents and red paths show innovative agents).
3.1.6 Interactions and communication
In models of team problem solving, communication can be modeled using organically timed pairwise interactions between team members (McComb et al.
Reference McComb, Cagan and Kotovsky2015). In KABOOM, agents collaborate and share solutions by sharing their current positions in the solution space with each other. While communication can be influenced by many social and individual factors (as in Patrashkova-Volzdoska et al.
Reference Patrashkova-Volzdoska, McComb, Green and Dale Compton2003; Singh et al.
Reference Singh, Dong and Gero2013), this work focuses specifically on the influence of cognitive style on communication. On a given turn, an agent can choose to either explore a new solution individually or communicate with another agent to share solutions. The probability of an agent choosing to communicate in a pairwise interaction on a given turn is set by a model parameter
![]() $c$
, which can be constant in time or change over time. On each turn, agents who decide to collaborate are paired randomly, regardless of their sub-team. While future work may give agents preferences for communicating with specific individuals, groups, or networks, the current model chooses the nominal case where any agent interacts with any other without preference. If there is an odd number of agents who wish to collaborate, the unpaired agent explores individually for that turn.
$c$
, which can be constant in time or change over time. On each turn, agents who decide to collaborate are paired randomly, regardless of their sub-team. While future work may give agents preferences for communicating with specific individuals, groups, or networks, the current model chooses the nominal case where any agent interacts with any other without preference. If there is an odd number of agents who wish to collaborate, the unpaired agent explores individually for that turn.
After sharing their current solutions, each agent evaluates the solution shared with them and chooses whether they want to move to that solution. As with evaluating a potential solution in individual exploration, the probability of accepting a solution that does not improve the objective function in favor of the current one is a stochastic function of the agent’s temperature (Equation (5)). When the temperature is zero, there is zero probability of choosing a solution that does not improve the objective function.
Research shows that when the difference in two people’s KAI total scores is greater than 20 points, communicating ideas with each other tends to become increasingly difficult (Kirton Reference Kirton2003). Agent collaboration in KABOOM reflects this increasing difficulty in communication due to the cognitive gap in style. In the model, communication between two agents always has some probability of failing; this likelihood is positively correlated with the difference between the agents’ KAI total scores (i.e., their cognitive style gap). This is implemented by requiring a uniformly distributed random variable to be less than the difference in two agents’ KAI total scores for successful communication. If communication is not successful, no information is shared between the agents, essentially resulting in a wasted iteration.
The probability of successful collaboration is:
 $$\begin{eqnarray}P=\left\{\begin{array}{@{}ll@{}}1,\quad & \text{if }\unicode[STIX]{x1D6E5}KAI\leqslant 10\\ 1-(\unicode[STIX]{x1D6E5}KAI-10)/170,\quad & \text{if }\unicode[STIX]{x1D6E5}KAI>10,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}P=\left\{\begin{array}{@{}ll@{}}1,\quad & \text{if }\unicode[STIX]{x1D6E5}KAI\leqslant 10\\ 1-(\unicode[STIX]{x1D6E5}KAI-10)/170,\quad & \text{if }\unicode[STIX]{x1D6E5}KAI>10,\end{array}\right.\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6E5}KAI$
is the difference between the two agents’ total KAI scores. Agents with KAI total score differences of 10 points or less have a 100% success rate, which drops linearly beyond the 10-point just-noticeable difference (JND) established in prior research (Kirton Reference Kirton2003). Communication across extremely large gaps of 100 points is modeled as only being successful 50% of the time (the observed KAI range is 109 points (Kirton Reference Kirton1976)).
$\unicode[STIX]{x1D6E5}KAI$
is the difference between the two agents’ total KAI scores. Agents with KAI total score differences of 10 points or less have a 100% success rate, which drops linearly beyond the 10-point just-noticeable difference (JND) established in prior research (Kirton Reference Kirton2003). Communication across extremely large gaps of 100 points is modeled as only being successful 50% of the time (the observed KAI range is 109 points (Kirton Reference Kirton1976)).
3.1.7 Team meetings
In addition to pairwise communication, agent teams have regularly scheduled meetings in which all team members converge to a single solution. First, the team creates an aggregate solution from the specialized sub-teams: each sub-team finds the best solution from any of its agents, then contributes only its dimensions to the aggregate team solution. For example, if there is a 2-dimensional solution space where sub-team 1 controls
![]() $x_{1}$
and sub-team 2 controls
$x_{1}$
and sub-team 2 controls
![]() $x_{2}$
, the aggregate solution is
$x_{2}$
, the aggregate solution is
![]() $\langle x_{1}\text{ from sub-team 1},x_{2}\text{ from sub-team 2}\rangle$
. Finally, all agents accept the new aggregate position, regardless of the quality of the new aggregate solution.
$\langle x_{1}\text{ from sub-team 1},x_{2}\text{ from sub-team 2}\rangle$
. Finally, all agents accept the new aggregate position, regardless of the quality of the new aggregate solution.
3.2 Creating a virtual population with KAI
We create a virtual population of individuals such that the distributions and correlations of KAI total scores (KAI total) and sub-scores (SO, E, and RG) reflect those of the general population. A Python script generates KAI scores and sub-scores for 10,000 virtual individuals from a multi-variate normal distribution. The mean, standard deviation, and correlations of KAI total, SO, E, and RG are based on a dataset of 597 individuals’ scores and sub-scores gathered in previous research (Jablokow Reference Jablokow2008). The sub-scores are all imperfectly correlated (
![]() $0.4<R^{2}<0.8$
) with the total KAI score. Because of this, even agents with the same KAI score will have different sub-scores for SO, E, and RG, meaning that any two agents with the same total KAI score are unlikely to be precisely identical in their style (as with humans). KABOOM draws from this virtual population to create agents with associated KAI scores. When the model requests an agent with a specific total KAI score (for instance, 95), it receives a randomly selected member from all individuals in the virtual population having the requested KAI score. Thus, requesting two agents with KAI total scores of 95 will return two different agents, each having total scores of 95 but (likely) having different sub-scores for SO, E, and RG.
$0.4<R^{2}<0.8$
) with the total KAI score. Because of this, even agents with the same KAI score will have different sub-scores for SO, E, and RG, meaning that any two agents with the same total KAI score are unlikely to be precisely identical in their style (as with humans). KABOOM draws from this virtual population to create agents with associated KAI scores. When the model requests an agent with a specific total KAI score (for instance, 95), it receives a randomly selected member from all individuals in the virtual population having the requested KAI score. Thus, requesting two agents with KAI total scores of 95 will return two different agents, each having total scores of 95 but (likely) having different sub-scores for SO, E, and RG.
3.2.1 Selecting agents for a team
When forming a team of agents, KABOOM can select individuals from the virtual population randomly or according to a team composition rule. This paper uses three team composition strategies:
(1) organic composition: team members are drawn randomly from a virtual population that is statistically representative of the true distribution of KAI scores;
(2) homogeneous composition: all team members have the same KAI total score (but likely have different sub-scores);
(3) linearly distributed heterogeneous composition: the team is composed with a given mean and range of KAI total scores. The team will be composed of agents linearly distributed across the range and centered on the mean. For example, a linearly distributed 5-person team with mean KAI of 100 and a range of 40 will be composed of five agents with KAI scores 80, 90, 100, 110, and 120.
When teams are divided into specialized sub-teams, each sub-team (rather than the full team) is selected to have a linearly distributed composition with the given mean and range. For example, given a team of 4 with 2 sub-teams of 2, and requiring a KAI mean of 100 and range of 40, each sub-team will be composed of two agents with KAI scores of 80 and 120.
It is worth noting that, in real management scenarios, managers often must compose new teams from a limited group of current employees. This scenario is explored in other work (Lapp, Jablokow & McComb Reference Lapp, Jablokow and McComb2019). In the current work, all teams are composed by drawing from the virtual population. When plots compare agents or homogeneous teams of three styles, the KAI scores are 55 (adaptive), 95 (mid-range), and 135 (innovative). These represent the 1.5th, 50th, and 98.5th percentiles of the population;
![]() $\text{KAI}=55$
and
$\text{KAI}=55$
and
![]() $\text{KAI}=135$
represent extremes of cognitive style behavior that are unlikely (but not impossible) to be observed in real life. These are intended to demonstrate the range of possible behaviors across the KAI spectrum. Organic composition gives more realistic team compositions.
$\text{KAI}=135$
represent extremes of cognitive style behavior that are unlikely (but not impossible) to be observed in real life. These are intended to demonstrate the range of possible behaviors across the KAI spectrum. Organic composition gives more realistic team compositions.
3.3 Objective functions
The design problem is represented by a scalar objective function
![]() $f(\vec{x})$
of
$f(\vec{x})$
of
![]() $n$
dimensions (variables). A solution defines the values of all variables, meaning a solution is a vector
$n$
dimensions (variables). A solution defines the values of all variables, meaning a solution is a vector
![]() $\vec{x}$
in the n-dimensional space. The quality of the solution is defined as the objective function’s value at that point,
$\vec{x}$
in the n-dimensional space. The quality of the solution is defined as the objective function’s value at that point,
![]() $f(\vec{x})$
. The goal is to maximize solution quality. Real-world problems can sometimes be formulated as analytic objective functions with several variables and constraints, as in Zurita et al. (Reference Zurita, Colby, Tumer, Hoyle and Tumer2017). However, this paper implements a more abstract mathematical objective function, so that it can be tuned and scaled in predictable ways. The objective function used throughout this paper is a summation of a quadratic function and a sinusoidal function in the form:
$f(\vec{x})$
. The goal is to maximize solution quality. Real-world problems can sometimes be formulated as analytic objective functions with several variables and constraints, as in Zurita et al. (Reference Zurita, Colby, Tumer, Hoyle and Tumer2017). However, this paper implements a more abstract mathematical objective function, so that it can be tuned and scaled in predictable ways. The objective function used throughout this paper is a summation of a quadratic function and a sinusoidal function in the form:
Figure 8 shows the objective function in one dimension for two values of
![]() $\unicode[STIX]{x1D6FC}$
. The objective function can be defined in any number of dimensions,
$\unicode[STIX]{x1D6FC}$
. The objective function can be defined in any number of dimensions,
![]() $n$
, and is symmetric in all dimensions. The oscillation frequency,
$n$
, and is symmetric in all dimensions. The oscillation frequency,
![]() $\unicode[STIX]{x1D714}$
, and quadratic coefficient,
$\unicode[STIX]{x1D714}$
, and quadratic coefficient,
![]() $C$
, are held constant. The space is bounded by
$C$
, are held constant. The space is bounded by
![]() $[-1,1]$
in all dimensions: solutions outside of this cube are infeasible. In order to focus on the relative performance of teams for a given problem, all performance axes for figures in this paper are normalized to the range of 0 to 1.
$[-1,1]$
in all dimensions: solutions outside of this cube are infeasible. In order to focus on the relative performance of teams for a given problem, all performance axes for figures in this paper are normalized to the range of 0 to 1.
This function is varied in two ways: (1) by scaling the independent variables in all dimensions using the scaling parameter,
![]() $\unicode[STIX]{x1D6FD}$
, and; (2) by scaling the amplitude of the sinusoid,
$\unicode[STIX]{x1D6FD}$
, and; (2) by scaling the amplitude of the sinusoid,
![]() $\unicode[STIX]{x1D6FC}$
. The first parameter affects the size of the search space, while the second parameter affects the amplitude of the sinusoid. Changing these two characteristic values creates a variety of different problems that may favor different cognitive styles.
$\unicode[STIX]{x1D6FC}$
. The first parameter affects the size of the search space, while the second parameter affects the amplitude of the sinusoid. Changing these two characteristic values creates a variety of different problems that may favor different cognitive styles.

Figure 8. The objective function is a composite of a sinusoid and a parabola. The oscillation amplitude
![]() $\unicode[STIX]{x1D6FC}$
of the objective function is varied from 0.22 to 5. Global exploration of the space is important when
$\unicode[STIX]{x1D6FC}$
of the objective function is varied from 0.22 to 5. Global exploration of the space is important when
![]() $\unicode[STIX]{x1D6FC}$
is small, but local exploitation is sufficient when
$\unicode[STIX]{x1D6FC}$
is small, but local exploitation is sufficient when
![]() $\unicode[STIX]{x1D6FC}$
is large. The vertical axis shows normalized solution quality.
$\unicode[STIX]{x1D6FC}$
is large. The vertical axis shows normalized solution quality.
3.4 Evaluating performance
At the end of the simulation, each team’s performance is the solution quality of the best solution any agent has had at any time during the simulation. Because the KABOOM model is stochastic, it repeats the same experiment 16 times (except where otherwise noted) before changing any parameters. However, due to the team selection methods described above, each repetition of the simulation uses a new team that is not composed of exactly the same agents. This is a standard Monte Carlo simulation approach, in which random instantiations enable the exploration of team performance across a variety of compositions. In this paper, plots of results show the mean and standard deviation of team performance with a dot and vertical error bar (shown in blue unless there are multiple series on one plot). In some plots, separate team scores from each repetition are shown as gray dots. Linear and quadratic best-fit equations are displayed as red curves.
3.5 Computational performance of the model
The Python implementation of KABOOM completes a simulation of 12 agents with 300 iterations and a 12-dimensional objective function in 4.1 s on a laptop with 16 gigabytes of RAM and a 2.5 GHz Intel Core i7 Processor. The Python implementation of KABOOM is available on GitHub.Footnote 1
4 Results
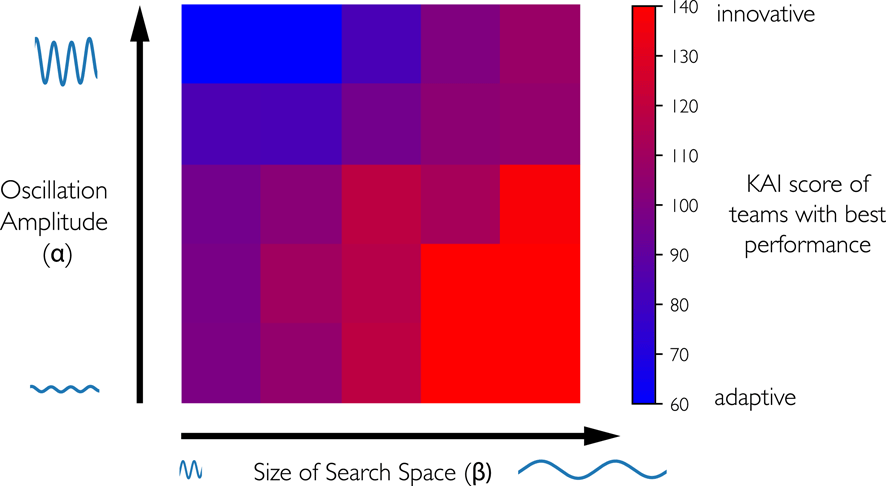
In this section, three studies examine how communication, specialization, and composition independently influence team performance for various cognitive style compositions. Communication refers to the frequency of pairwise solution sharing and the frequency of team meetings. The first study shows that while pairwise communication can often help performance, the optimal communication rate depends strongly on the cognitive style of the team. Specialization refers to the division of the team into sub-teams which tackle pieces of the problem independently. Results from the specialization study suggest that the optimal amount of team specialization depends strongly on the cognitive styles of its members. Finally, twenty-five variations of the problem are created to test how differences in the problem affect the performance of agents with different cognitive styles. The performance of a team is measured by the objective function’s value for the best solution any agent on the team has found through the course of the simulation.
4.1 Communication: pairwise communication frequency
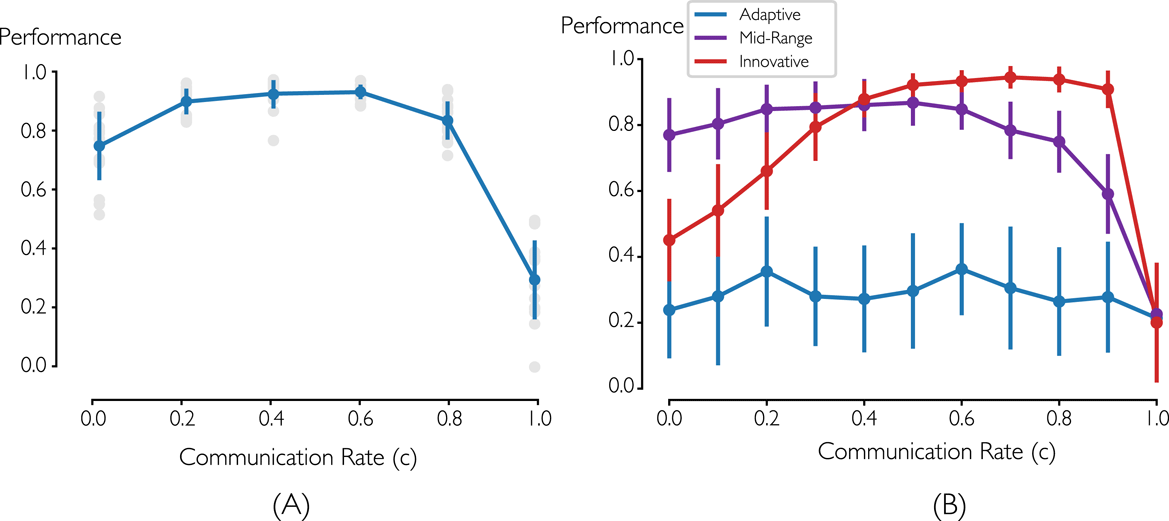
Pairwise communication is driven by agents’ desired communication frequency and has organic timing. Our first study examined how the frequency of pairwise communication affects performance. Results of previous work suggest that there is a curvilinear (rather than linear) relationship between communication and performance, meaning that the best performance will occur at some intermediate communication rate, above which performance will decrease (Patrashkova-Volzdoska et al. Reference Patrashkova-Volzdoska, McComb, Green and Dale Compton2003; Patrashkova & McComb Reference Patrashkova and McComb2004; McComb et al. Reference McComb, Cagan and Kotovsky2017a ).
We call the agents’ rate of pairwise communication the “communication policy”
![]() $c$
. At each iteration, every agent in the simulation chooses to collaborate with another agent with probability according to the communication policy
$c$
. At each iteration, every agent in the simulation chooses to collaborate with another agent with probability according to the communication policy
![]() $c$
, or to explore individually with probability
$c$
, or to explore individually with probability
![]() $1-c$
. Varying
$1-c$
. Varying
![]() $c$
from zero to one represents the spectrum of strategies from individual exploration with no pairwise communication (
$c$
from zero to one represents the spectrum of strategies from individual exploration with no pairwise communication (
![]() $c=0$
) to constant communication with no exploration (
$c=0$
) to constant communication with no exploration (
![]() $c=1$
).
$c=1$
).
Figure 9(A) shows the performance of teams with organic composition (12 agents per team, 4 sub-teams of 3) for a range of communication policies. Each gray dot represents one team’s final solution quality. The blue points and lines indicate the mean and one standard deviation for the eight teams’ respective performance with a given communication policy. It is clear that there is a curvilinear relationship involved, where communication improves performance up to a point and then diminishes performance. (Performance drops significantly for
![]() $c=1$
, because agents never explore the solution space.) The optimal policy for this problem and team is to have a 40% to 60% chance of trying to collaborate on each turn. This result is consistent when testing with different team sizes and specializations.
$c=1$
, because agents never explore the solution space.) The optimal policy for this problem and team is to have a 40% to 60% chance of trying to collaborate on each turn. This result is consistent when testing with different team sizes and specializations.
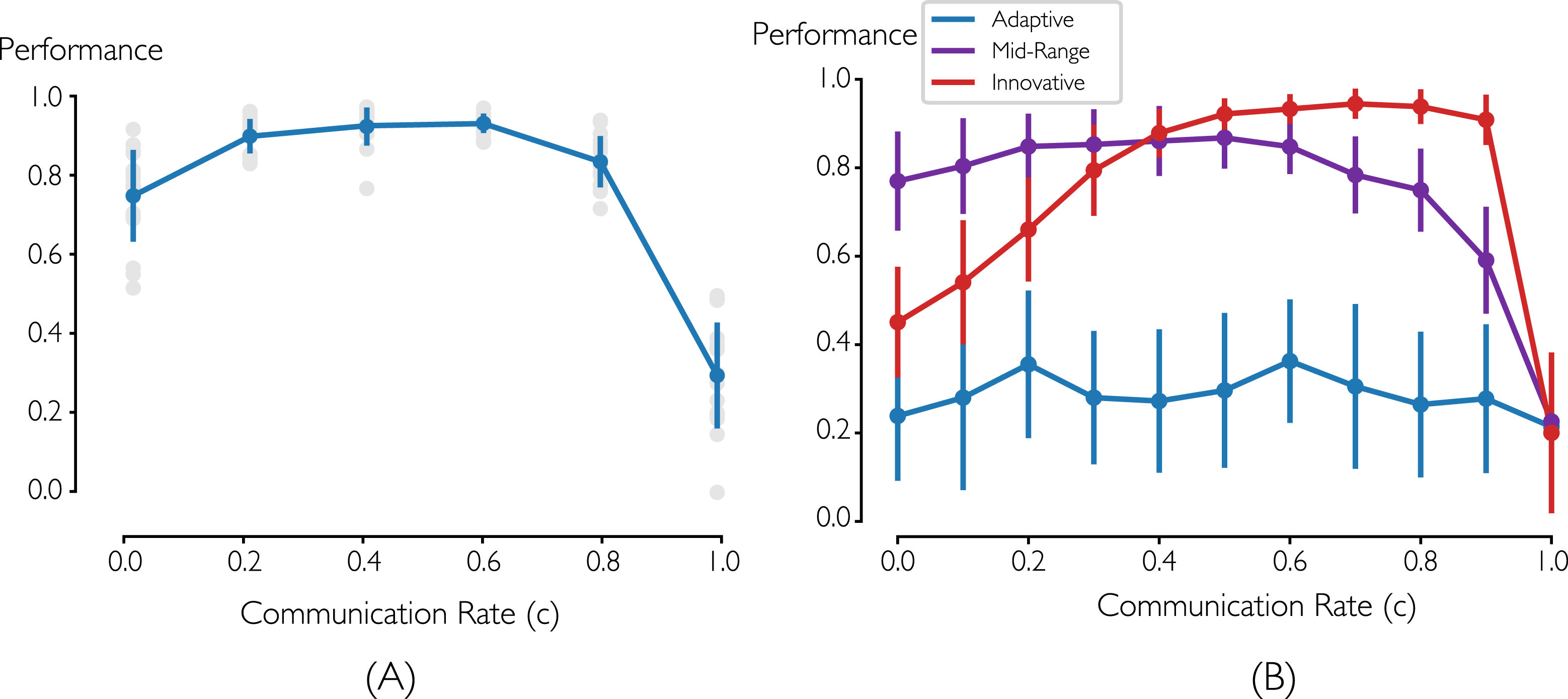
Figure 9. (A) Trade-off of pairwise communication frequency with team performance of 12-agent team with 4 sub-teams. (B) Effect of communication frequency on team performance for homogeneous teams of adaptive, mid-range, and innovative style (in both plots, error bars indicate
![]() $\pm 1$
standard deviation).
$\pm 1$
standard deviation).
The optimal communication policy changes drastically for homogeneous teams of different cognitive styles (Figure 9(B)). For a homogeneous team with a shared innovative style, increasing the communication rate increases performance up to very high values (
![]() $c=0.8$
). Compared to the effect on homogeneous innovative teams, the effect of communication is much weaker for the homogeneous adaptive teams, but there is a boost in performance at 0.2 and 0.6. The homogeneous mid-range team performs best for
$c=0.8$
). Compared to the effect on homogeneous innovative teams, the effect of communication is much weaker for the homogeneous adaptive teams, but there is a boost in performance at 0.2 and 0.6. The homogeneous mid-range team performs best for
![]() $c$
around 0.4, similar to the organic teams.
$c$
around 0.4, similar to the organic teams.
The performance of homogeneous innovative teams with high rates of communication (
![]() $0.5<c<0.9$
) has a smaller standard deviation, as well as a higher average score. We can interpret this result by considering the balance of exploration (broad search) and exploitation (local refinement of a solution). An innovative team has little difficulty exploring the space, but they will not converge and refine the best solutions unless the team members interact very frequently, effectively “bringing themselves back” to the original problem-solving aim. For mid-range homogeneous teams, convergence and exploitation happen more easily, but too much time spent on pairwise communication (
$0.5<c<0.9$
) has a smaller standard deviation, as well as a higher average score. We can interpret this result by considering the balance of exploration (broad search) and exploitation (local refinement of a solution). An innovative team has little difficulty exploring the space, but they will not converge and refine the best solutions unless the team members interact very frequently, effectively “bringing themselves back” to the original problem-solving aim. For mid-range homogeneous teams, convergence and exploitation happen more easily, but too much time spent on pairwise communication (
![]() $c>0.6$
) inhibits thorough exploration. For more adaptive homogeneous teams, performance is less dependent on communication frequency, as more adaptive teams tend to reach consensus early and then stick to the approach they have agreed upon, which tends to focus on refining the best solutions by default. These results agree well with a human-subjects study on Adaption–Innovation style and team network structures (Carnabuci & Dioszegi Reference Carnabuci and Dioszegi2015). That study found that adaptors performed best in loosely connected networks with structural holes, while innovators performed best in densely connected networks.
$c>0.6$
) inhibits thorough exploration. For more adaptive homogeneous teams, performance is less dependent on communication frequency, as more adaptive teams tend to reach consensus early and then stick to the approach they have agreed upon, which tends to focus on refining the best solutions by default. These results agree well with a human-subjects study on Adaption–Innovation style and team network structures (Carnabuci & Dioszegi Reference Carnabuci and Dioszegi2015). That study found that adaptors performed best in loosely connected networks with structural holes, while innovators performed best in densely connected networks.
Table 2. Specialized teams decompose a problem by dividing the dimensions among sub-teams.

4.2 Specialization: number of specialized sub-teams
KABOOM can rapidly simulate team performance for many different team compositions and sub-team specialization configurations, giving insight into potential strategies for team organization. To demonstrate KABOOM’s ability to study a wide range of scenarios, this section reports on the optimal amount of specialization in a team for different team sizes and style compositions.
Engineering teams often specialize by breaking a problem into (semi)independent pieces and assigning different parts of the problem to sub-teams (Austin-Breneman, Yu & Yang Reference Austin-Breneman, Yu and Yang2015). For example, a team designing a rocket might have sub-teams working on propulsion, stability, and aerodynamics. In the context of this research, specialization refers to the number of sub-teams working on independent aspects of a problem. The ‘independent aspects of a problem’ correspond to mutually exclusive sets of dimensions. This assumes a perfect decomposition of the variables of the problem, which is not always possible. However, this assumption allows KABOOM to study the effects of problem decomposition as a measure of team specialization. The agents on a team are evenly distributed across the sub-teams. For example, a team of six agents might be organized as one flat team of six agents, two sub-teams of three, three sub-teams of two, or six individuals all working on independent aspects of the problem. Each sub-team is specialized in that it controls a subset of all the dimensions in the problem. Table 2 illustrates how a 6-agent team would divide a 6-dimensional problem among sub-teams for different amounts of team specialization. Note that with regard to problem decomposition, six individuals working on six sub-teams (complete specialization) represents a distinct scenario from all six individuals working on 1 sub-team (no specialization).
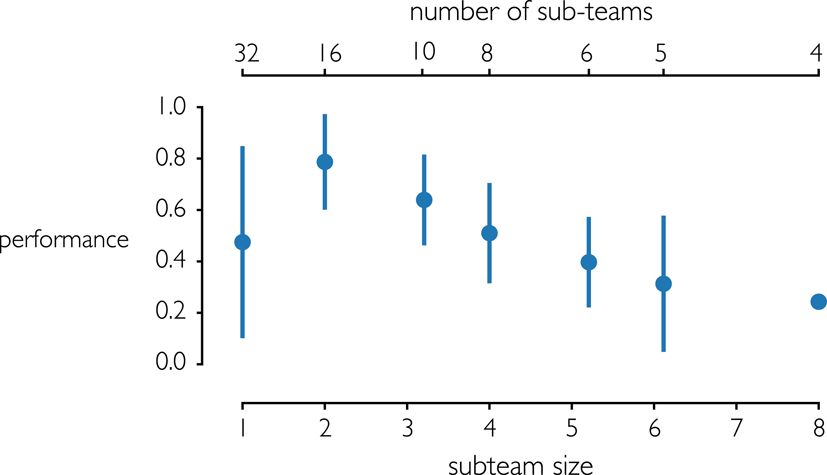
To demonstrate the effect of specialization on performance, Figure 10 shows the optimal amount of specialization for 32-agent teams of organic composition. The bottom horizontal axis shows the number of agents per team, while the top horizontal axis shows the number of sub-teams. (Team size and number of agents per team determine the number of sub-teams.) The optimal specialization for 32-agent teams or organic composition is sixteen sub-teams (pairs) of two agents. For cases in which the number of agents is not evenly divisible by the number of sub-teams, the sub-teams are not all equal in size. For instance, 32 agents cannot be equally divided into 10 sub-teams. In that case, the team was composed of 8 sub-teams of 3 agents and 2 sub-teams of 4 agents. Approximations of this nature are necessary for teams composed of 10, 6, and 5 sub-teams.
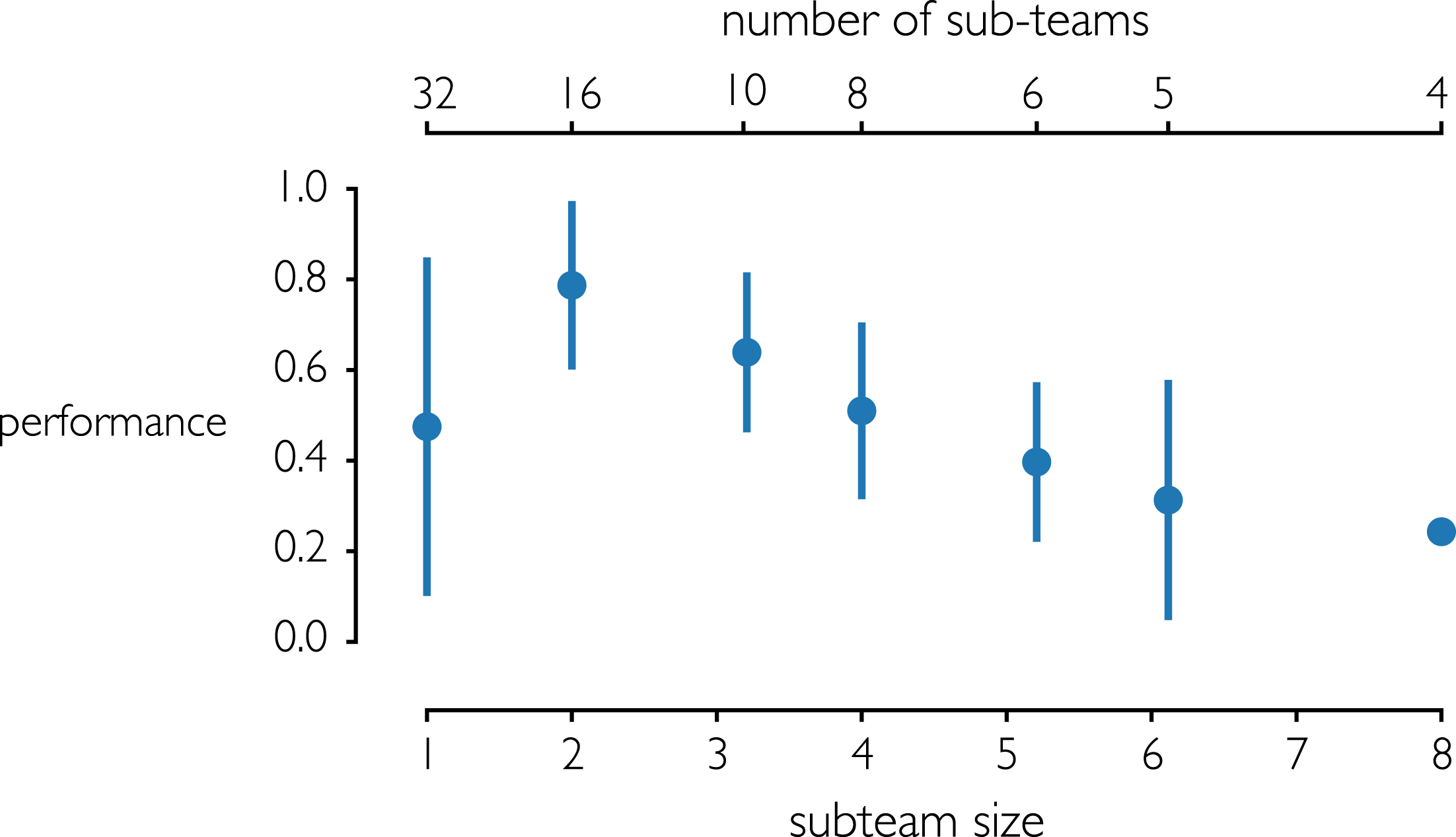
Figure 10. Performance of teams of 32 agents with organic composition, for different levels of team specialization (error bars indicate
![]() $\pm 1$
standard deviation). For cases in which the number of agents is not evenly divisible by the number of sub-teams, the sub-teams are not all equal in size.
$\pm 1$
standard deviation). For cases in which the number of agents is not evenly divisible by the number of sub-teams, the sub-teams are not all equal in size.
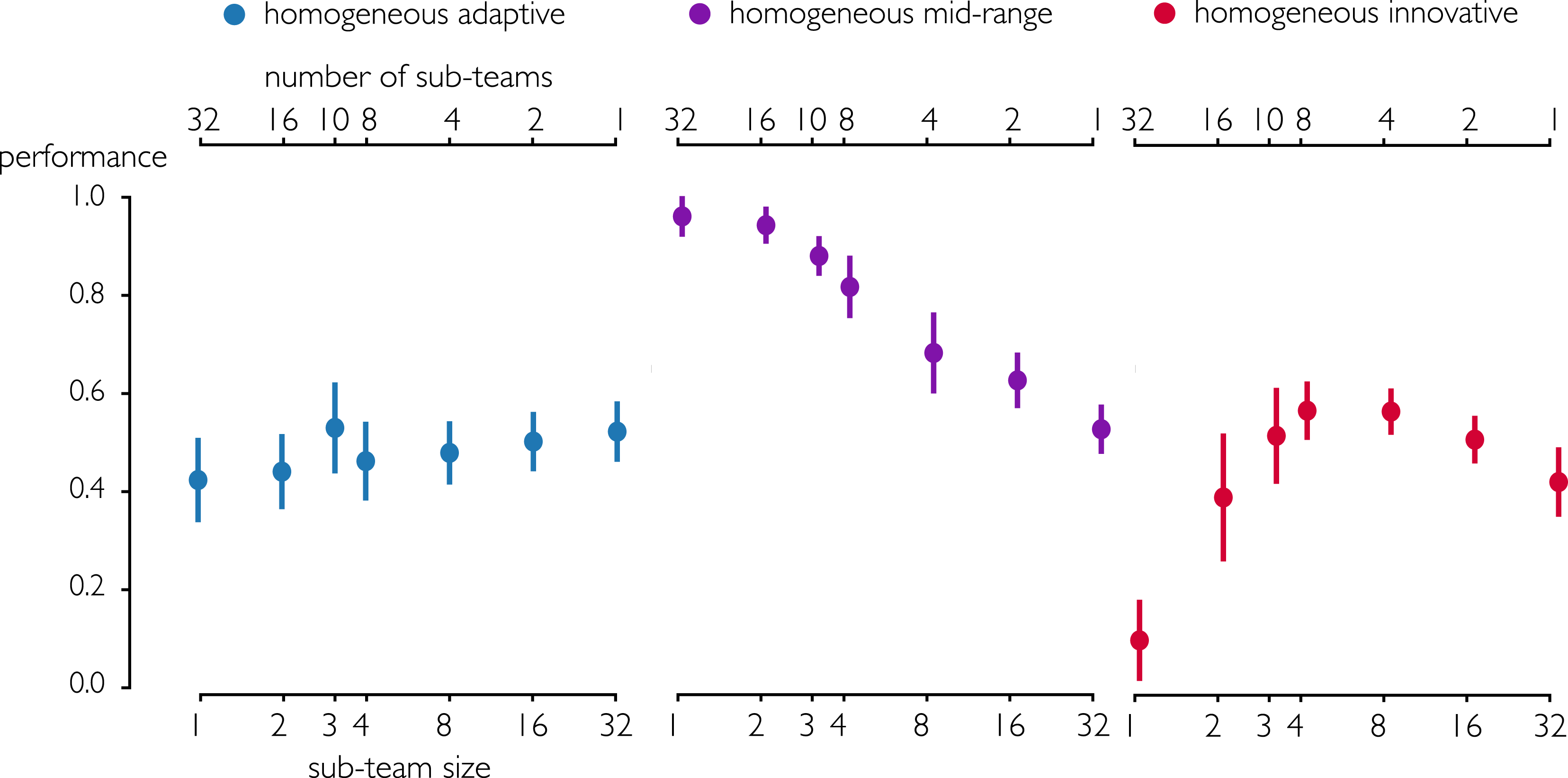
Figure 11. Performance versus specialization for three homogeneous teams of different KAI cognitive styles (error bars indicate
![]() $\pm 1$
standard deviation). For cases in which the number of agents is not evenly divisible by the number of sub-teams, the sub-teams are not all equal in size.
$\pm 1$
standard deviation). For cases in which the number of agents is not evenly divisible by the number of sub-teams, the sub-teams are not all equal in size.
The next investigation explores whether cognitive style affects the optimal amount of team specialization. We use the null hypothesis that the cognitive styles of agents on the team will not affect the optimal amount of specialization. Figure 11 shows the same study as above, but with homogeneous teams of more innovative, more adaptive, and mid-range styles rather than organically composed teams. The optimal specialization was significantly different for the three types of teams (Figure 11). The innovative teams perform best in larger sub-teams of four or eight agents, while the mid-range teams perform best with complete specialization (32 teams of one agent each), and the adaptive teams showed less dependence on specialization but perform best with three agents.
These results suggest that it may be important to consider the styles of team members when deciding how and how much to divide a team into specialized sub-teams. Specifically, the model predicts that a homogeneous team of more innovative individuals will perform poorly with small, highly specialized sub-teams. This result is consistent for problems with different values of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
(the objective function parameters). Complete specialization into 1-person sub-teams requires a high level of trust in each agent’s performance, because every agent will contribute to the team’s aggregate solution. However, innovative agents tend to perform less predictably (i.e., sometimes poorly and sometimes well), making it easier for smaller innovative sub-teams to go off track. Having larger teams of four to eight innovators allows the full team to take the best solution of one agent on each sub-team and discard lower quality solutions.
$\unicode[STIX]{x1D6FD}$
(the objective function parameters). Complete specialization into 1-person sub-teams requires a high level of trust in each agent’s performance, because every agent will contribute to the team’s aggregate solution. However, innovative agents tend to perform less predictably (i.e., sometimes poorly and sometimes well), making it easier for smaller innovative sub-teams to go off track. Having larger teams of four to eight innovators allows the full team to take the best solution of one agent on each sub-team and discard lower quality solutions.
Mid-range teams, on the other hand, perform best with complete specialization into one-person sub-teams. These agents do not explore radical solutions in potentially damaging ways, but they do explore the space sufficiently to find good solutions. This trend reflects the results of Blackburn, Lapre & Van Wassenhove (Reference Blackburn, Lapre and Van Wassenhove2006), a study of software development teams which concluded that increasing team size decreased productivity. Finally, homogeneous adaptive teams do not explore radical solutions that could result in poor performance, but they also do not explore the solution space sufficiently to find high-quality solutions. The effect of team specialization on their performance is small, which is likely a result (once again) of the high degree of consistency found within adaptive teams due to their preference for consensual decision-making. In future work, human-subjects studies will be needed to test the hypotheses suggested by all of these results – i.e., for more adaptive, more innovative, and mid-range teams of various amounts of specialization.
4.3 Composition: performance of homogeneous style teams on diverse problems
This section analyzes the performance of homogeneous teams of different shared KAI total scores on a matrix of 25 problems. These problems were created by modifying the objective function parameters – i.e., by permuting five logarithmically spaced values for
![]() $\unicode[STIX]{x1D6FC}$
and five logarithmically spaced values for
$\unicode[STIX]{x1D6FC}$
and five logarithmically spaced values for
![]() $\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}$
.
The first parameter (
![]() $\unicode[STIX]{x1D6FC}$
) affects the amplitude of the sinusoid (Figure 8). When the amplitude is large relative to the quadratic function, the quadratic becomes negligible, so that optimizing any local minimum yields similar performance to finding the global minimum. On the other hand, when the amplitude is small, the quadratic function becomes important in the cost function, so that finding the global local minimum is much better than finding a distant local minimum. Because large-amplitude problems reward local exploration, while small-amplitude problems reward global exploration, we hypothesize that more adaptive agents (lower KAI scores) will outperform other styles on large-amplitude problems (large
$\unicode[STIX]{x1D6FC}$
) affects the amplitude of the sinusoid (Figure 8). When the amplitude is large relative to the quadratic function, the quadratic becomes negligible, so that optimizing any local minimum yields similar performance to finding the global minimum. On the other hand, when the amplitude is small, the quadratic function becomes important in the cost function, so that finding the global local minimum is much better than finding a distant local minimum. Because large-amplitude problems reward local exploration, while small-amplitude problems reward global exploration, we hypothesize that more adaptive agents (lower KAI scores) will outperform other styles on large-amplitude problems (large
![]() $\unicode[STIX]{x1D6FC}$
), while more innovative agents (higher KAI scores) will have an advantage in small-amplitude (small
$\unicode[STIX]{x1D6FC}$
), while more innovative agents (higher KAI scores) will have an advantage in small-amplitude (small
![]() $\unicode[STIX]{x1D6FC}$
) problems. The second parameter (
$\unicode[STIX]{x1D6FC}$
) problems. The second parameter (
![]() $\unicode[STIX]{x1D6FD}$
) affects the size of the search space. Large search spaces require broader search strategies and more stochastic methods, corresponding to higher temperature in a simulated-annealing paradigm (Kirkpatrick et al.
Reference Kirkpatrick, Gelatt and Vecchi1983). Therefore, we hypothesize that higher (more innovative) KAI scores will be advantageous for large search spaces (large
$\unicode[STIX]{x1D6FD}$
) affects the size of the search space. Large search spaces require broader search strategies and more stochastic methods, corresponding to higher temperature in a simulated-annealing paradigm (Kirkpatrick et al.
Reference Kirkpatrick, Gelatt and Vecchi1983). Therefore, we hypothesize that higher (more innovative) KAI scores will be advantageous for large search spaces (large
![]() $\unicode[STIX]{x1D6FD}$
), while lower (more adaptive) KAI scores will have an advantage in small search spaces (small
$\unicode[STIX]{x1D6FD}$
), while lower (more adaptive) KAI scores will have an advantage in small search spaces (small
![]() $\unicode[STIX]{x1D6FD}$
), with mid-range KAI scores having an advantage in between.
$\unicode[STIX]{x1D6FD}$
), with mid-range KAI scores having an advantage in between.
Homogeneous teams of more adaptive, more innovative, and mid-range styles, respectively, were tested on the 25 problems. Each combination of
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D6FD}$
, and shared KAI score was repeated only 8 times due to the large number of combinations. Figure 12 shows the optimal style of a homogeneous team on the KAI spectrum for each problem (from red as the most innovative homogeneous team to blue as the most adaptive homogeneous team). The optimal style of the problems ranges from highly innovative in the upper-left corner (large search space, small sinusoidal amplitude), to mid-range, to highly adaptive in the lower-right corner (small search space, large sinusoidal amplitude).
$\unicode[STIX]{x1D6FD}$
, and shared KAI score was repeated only 8 times due to the large number of combinations. Figure 12 shows the optimal style of a homogeneous team on the KAI spectrum for each problem (from red as the most innovative homogeneous team to blue as the most adaptive homogeneous team). The optimal style of the problems ranges from highly innovative in the upper-left corner (large search space, small sinusoidal amplitude), to mid-range, to highly adaptive in the lower-right corner (small search space, large sinusoidal amplitude).
Both our hypotheses about the alignment of shared team cognitive style and problem characteristics proved to be correct: larger search spaces favor innovators, and larger sinusoidal amplitudes favor adaptors. The combined effect of the two problem variables is that extreme innovators perform best for problems with small
![]() $\unicode[STIX]{x1D6FC}$
and large
$\unicode[STIX]{x1D6FC}$
and large
![]() $\unicode[STIX]{x1D6FD}$
(lower-right corner of the figure), extreme adaptors perform best for problems with large
$\unicode[STIX]{x1D6FD}$
(lower-right corner of the figure), extreme adaptors perform best for problems with large
![]() $\unicode[STIX]{x1D6FC}$
and small
$\unicode[STIX]{x1D6FC}$
and small
![]() $\unicode[STIX]{x1D6FD}$
(upper left), and mid-range styles perform best on other combinations of
$\unicode[STIX]{x1D6FD}$
(upper left), and mid-range styles perform best on other combinations of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
. It is worth noting that there are some problems where having a mid-range style is advantageous over a more adaptive or more innovative style, which validates the importance of remembering that cognitive style is continuous, rather than a dichotomy of two “types” (Kirton Reference Kirton2003).
$\unicode[STIX]{x1D6FD}$
. It is worth noting that there are some problems where having a mid-range style is advantageous over a more adaptive or more innovative style, which validates the importance of remembering that cognitive style is continuous, rather than a dichotomy of two “types” (Kirton Reference Kirton2003).
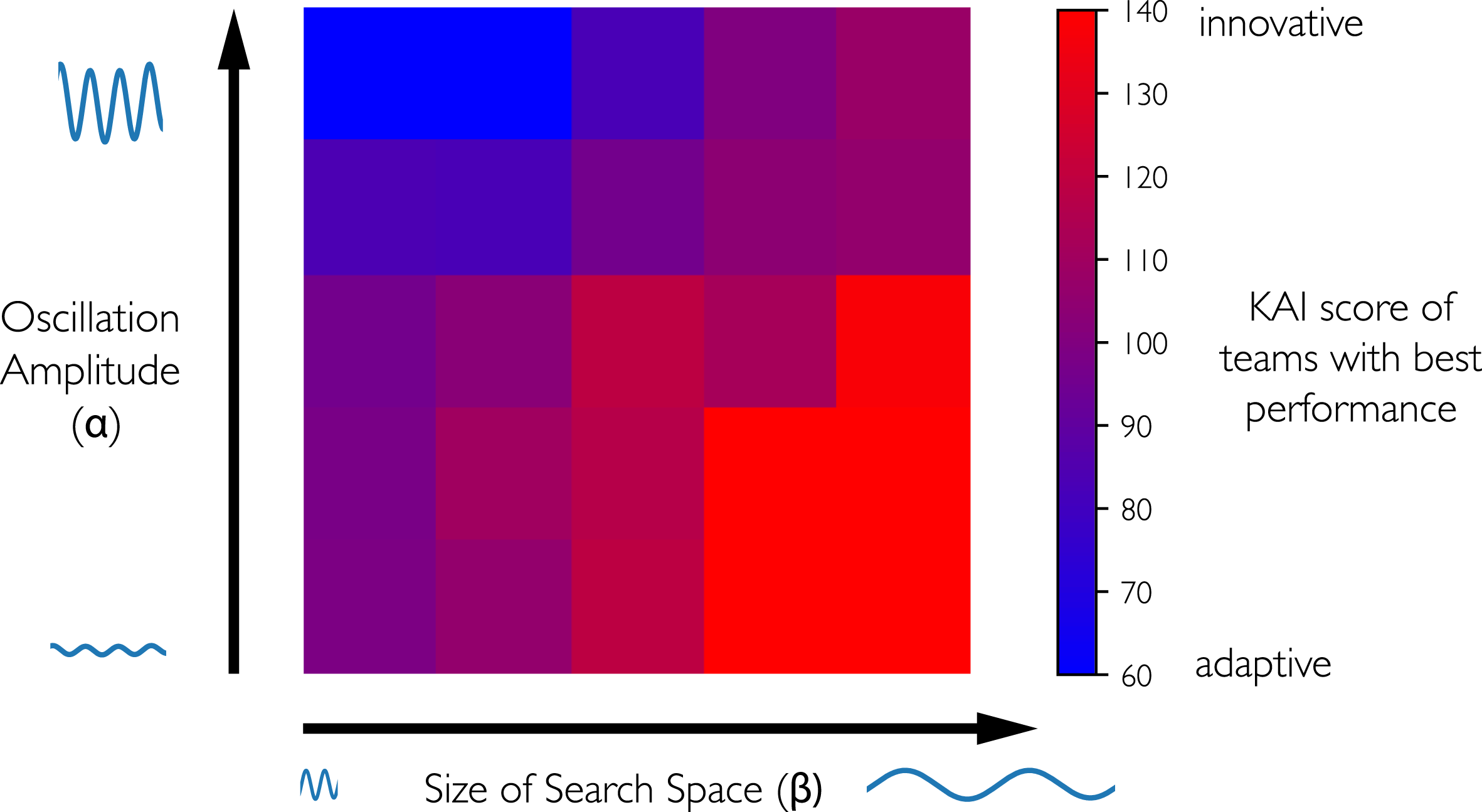
Figure 12. Homogeneous teams of different KAI styles were tested on each of 25 problems, with varying
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
. Color indicates the best-performing style for each problem from blue (more adaptive) to red (more innovative).
$\unicode[STIX]{x1D6FD}$
. Color indicates the best-performing style for each problem from blue (more adaptive) to red (more innovative).
The
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
parameters of the simulated problems are loosely related to the characteristics of real-life problems that make them better suited for adaptive or innovative approaches. The oscillation amplitude
$\unicode[STIX]{x1D6FD}$
parameters of the simulated problems are loosely related to the characteristics of real-life problems that make them better suited for adaptive or innovative approaches. The oscillation amplitude
![]() $\unicode[STIX]{x1D6FC}$
aligns with the importance of global exploration versus local exploitation. Real-world design problems focused on new product development generally require broad exploration (as in designing a new children’s toy), while redesigns and improvements of existing designs require thorough local exploration (as in improving the efficiency of an internal combustion engine). The effective solution space size
$\unicode[STIX]{x1D6FC}$
aligns with the importance of global exploration versus local exploitation. Real-world design problems focused on new product development generally require broad exploration (as in designing a new children’s toy), while redesigns and improvements of existing designs require thorough local exploration (as in improving the efficiency of an internal combustion engine). The effective solution space size
![]() $\unicode[STIX]{x1D6FD}$
corresponds to the number of iterations required to explore a space given a constant step size. Real-world problems may have small solution spaces when there are few variables, when variables only take a limited number of discrete values, or when there are a small number of distinguishable solutions. Conversely, problems can have large solution spaces when they have many dimensions or continuous variables with many distinguishable values. For example, a traveling salesman problem (Applegate, Bixby & Chvátal Reference Applegate, Bixby and Chvátal2007) may have a small solution space if it only has a few nodes, but a very large solution space if it has many nodes. Future work will incorporate contextualized design problems in the model to better understand the links between computational objective functions and real-world problems.
$\unicode[STIX]{x1D6FD}$
corresponds to the number of iterations required to explore a space given a constant step size. Real-world problems may have small solution spaces when there are few variables, when variables only take a limited number of discrete values, or when there are a small number of distinguishable solutions. Conversely, problems can have large solution spaces when they have many dimensions or continuous variables with many distinguishable values. For example, a traveling salesman problem (Applegate, Bixby & Chvátal Reference Applegate, Bixby and Chvátal2007) may have a small solution space if it only has a few nodes, but a very large solution space if it has many nodes. Future work will incorporate contextualized design problems in the model to better understand the links between computational objective functions and real-world problems.
5 Limitations
The KABOOM model focuses on specific characteristics of cognitive style and team problem solving; it does not create a comprehensive representation of team problem solving. Because of this, there are several major limitations of the current model. With regard to cognitive style, the model attempts to map specific human problem-solving characteristics to parameters in the model (i.e. mapping the diversity of people’s solutions to the step size and temperature in a simulated-annealing framework). Cognitive style and behavior are extremely complex, and many important effects of style have not been modeled. For instance, KABOOM does not attempt to model the coping behaviors that people of different styles may use when working together. Because modeling all aspects of human behavior would be unfeasible, we were forced to choose which aspects of behavior were most important to team performance outcomes and to envision how they would map onto quantitative parameters in the model.
The model’s reflection of communication, collaboration, and specialization are also limited. Previous work has focused extensively on modeling communication and collaboration within teams (Patrashkova-Volzdoska et al. Reference Patrashkova-Volzdoska, McComb, Green and Dale Compton2003; Fan & Yen Reference Fan and Yen2004; Patrashkova & McComb Reference Patrashkova and McComb2004; Tsvetovat & Carley Reference Tsvetovat and Carley2004; Singh et al. Reference Singh, Dong and Gero2013; Bernstein et al. Reference Bernstein, Shore and Lazer2018), resulting in models with much more complex mechanisms for communication than those in KABOOM. In real teams, people communicate ideas about process, strategy, sentiment, and emotion, while agents in KABOOM only communicate their solutions. While more complex models of communication could be incorporated into KABOOM, the mechanisms implemented for pairwise solution sharing and team convergence with meetings were sufficient to recreate the communication trade-offs observed in the literature. Likewise, previous work has developed more complex constructs for team specialization that incorporate communication patterns, domain knowledge, and heterogeneous cognitive abilities (Fan & Yen Reference Fan and Yen2004; Hulse et al. Reference Hulse, Gigous, Tumer, Hoyle and Tumer2017, Reference Hulse, Tumer, Hoyle and Tumer2018). In KABOOM, specialization is treated simply as a problem decomposition, which may be an over-simplification of how organizational structure shapes team performance.
Further, this work only tests KABOOM with one parameterized design problem that is abstract and hard to relate to real-world problems. The model has the capacity to study any design problem that can be posed as an objective function, but additional problems were beyond the scope of this paper. Because the experiments from this paper are all based on a set of closely related objective functions that does not model a real-world problem, their results cannot be directly compared to real-world design teams or solutions. Future studies will incorporate contextualized real-world design problems into KABOOM to provide more direct comparison to real-world scenarios.
The lack of any human-subjects research to test the validity of results from the model is another important limitation of the current work. Without support from human-subjects validation studies, the results presented in this paper cannot be assumed to hold true in real-life scenarios. Future work will focus on validating model results with human-subjects studies. All of these limitations are a reminder that this model is an early experiment in the direction of simulating human cognitive style with agent-based modeling. The results from this new model are as much demonstration of the method’s capabilities for studying teamwork as they are predictions of real-world behavior. The limitations noted here also lay the groundwork for the future work described below.
6 Future work
This section first addresses future work specific to KABOOM and then more broadly outlines future work for the field of design science. First, future work on KABOOM should focus on (1) validating the results of the agent-based model with human-subjects research; (2) enhancing the cognitive and social complexity of the agents to more closely reflect human activity; and (3) mapping between real-world and mathematically defined problems. Results from the model have the potential to inform the design of focused case studies that test specific hypotheses about team behavior and performance. For instance, a human-subjects study could test the hypothesis that homogeneous teams of innovators will perform best with very frequent communication, while homogeneous teams of mid-range agents will perform best with less communication (as in Figure 9(B)). Discrepancies between real-world behavior and model behavior can then inform the refinement of the model through tuning of parameters, addition of higher-level cognitive processes, and adjustment of the fundamental behavioral rules used in the model.
KABOOM could also be expanded to include more complex behaviors, as seen in other contemporary models. For instance, the model could adopt social networking patterns as in Singh et al. (Reference Singh, Dong and Gero2013). Moreover, coping behavior the temporary adjustments in behavior that people make to bridge large cognitive style gaps could be incorporated into agents’ behavior. The agents could also be given learning strategies such as sequence learning, as in McComb et al. (Reference McComb, Cagan and Kotovsky2017b ). These modifications could result in a more nuanced model of team performance and behavior with greater predictive power.
Another important direction of future work is to establish an approach to map between the mathematically defined problems commonly used in a simulation and real-world problems that are often messy and ill-defined. Using an objective function that is contextualized within a realistic problem can allow simulation results to be compared more easily to human-subjects tests on the same problem. For example, McComb et al. (Reference McComb, Cagan and Kotovsky2015) directly compare trusses designed by humans in a cognitive study and virtual agents in the CISAT simulation. However, real-world design problems are generally ill-defined, and solutions often cannot be represented by a set of quantitative design variables. These ill-defined problems might be simulated by imposing the mathematical structure seen in simulated problems, but this inherently locks the problem into a single representation. Therefore, future work will need to develop a method of mapping between simulated problems and real-world problems without imposing a strictly defined mathematical structure. This is critical for transferring the results of computational simulations into real-world practice.
More broadly, a better understanding of design teams can be achieved through a variety of future research directions in the field of design science. First, simulations should strive to model individual differences between people, rather than assuming people are homogeneous. These differences are not limited to cognitive style and could include individual traits such as learning ability, background knowledge, social connectedness, or personality. Next, future work will need to explore the relationships between these individual traits and attributes of a design problem. These relationships will help to predict an individual’s performance on a specific problem, which could be used for determining team composition.
One of the main attractions of simulation is the ability to rapidly explore large numbers of hypothetical scenarios at relatively low cost. This strength should be leveraged in research to explore many scenarios in simulation before investing in human-subjects experimentation. Through this hybrid approach, modeling can act as an early prototyping phase, where many scenarios are considered and those with the greatest potential for knowledge creation are selected for human-subjects studies. However, the benefits of this approach may extend far beyond academia. Given high-performance simulation models of design teams, many industries will be able to incorporate simulation into their human resources and management practices. By simulating thousands of teams before actually assembling one, organizations will be able to create more successful teams more reliably, leading to significant savings in cost and increases in productivity.
7 Conclusion
This paper introduced KABOOM, the first team simulation modeling framework to reflect the diverse range of human cognitive styles. In KABOOM, the behaviors of heterogeneous agents simulate the range of cognitive styles described by the Kirton Adaption-Innovation spectrum. The primary objectives of this research were to create an agent-based model incorporating cognitive style, analyze the effects of style on problem-solving performance, and explore the interactions of style with team composition, specialization, and communication. The development of cognitive style in the simulated agents took inspiration from research in psychology, sociology, design science, and the Kirton Adaption-Innovation theory to reflect empirically observed human behaviors. The resulting model successfully simulated a range of distinct behaviors driven by cognitive style. In KABOOM simulations, the behavior of more adaptive, mid-range, and more innovative agents generally reflected the intended behavior and resulted in patterns in performance that were sometimes non-intuitive. The key hypotheses derived from the computational experiments are as follows:
(1) The optimal communication rate for innovative teams is higher than that of adaptive and mid-range teams.
(2) Extreme specialization benefits mid-range teams but can be harmful for innovative teams.
(3) The optimal cognitive style for a problem depends on the size of the solution space and importance of global exploration.
Table 3. Model parameters for all figures

While this work has focused on developing a flexible simulation framework, future work will validate and further develop the model through a targeted set of human studies. The most powerful models and insights are likely to result from a hybrid research approach that merges the breadth and flexibility of computational simulation with the validation and holistic reality of human studies. The human studies will not only test the validity of insights provided by the model, but will also serve as a feedback loop for tuning and improving the behavior of agents in the model. Likewise, insights from the model will guide the development of human studies designed to examine specific hypotheses about behavior, teamwork, and cognitive style, which could lead to novel insights on social and cognitive behaviors. In time, the mutual feedback between in vivo and in silico scientific investigations will lead to a deeper understanding of the cognitive processes underlying design, and how those processes influence the behaviors of individuals and teams. By allowing computational agents to embody unique cognitive styles, this model opens the door to a future of design analysis built at the intersection of computer precision and human individuality.
Acknowledgments
This research was supported with funding from the School of Engineering Design, Technology, and Professional Programs at The Pennsylvania State University.
Appendix. Parameters table
Table 3 lists the parameters used for each figure in the paper. The value var indicates that the parameter was an independent variable in the figure. Style composition is indicated by h (homogeneous) or o (organic). Except when noted explicitly in the figure, homogeneous teams had a KAI score of 95 (the observed mean).